Красивые» задачи по содержанию

Россия, Ханты-Мансийский автономный округ-Югра, г. Урай

Автор:

Леонтьева Евгения Игоревна,

МОУ «Гимназия», 10Б класс

Научный руководитель:

Казанцева Надежда Аркадьевна, учитель математики,

МОУ «Гимназия»

«КРАСИВЫЕ» ЗАДАЧИ В МАТЕМАТИКЕ

Леонтьева Евгения Игоревна,

Россия, Тюменская область,

Ханты-Мансийский автономный округ-Югра, г.Урай,

Муниципальное общеобразовательное учреждение «Гимназия»,

Б класс

НАУЧНАЯ СТАТЬЯ

ОГЛАВЛЕНИЕ

Введение

Глава I……………………………………………………………………………… 3

1.1 «Красота» в математике………………………………………………………… 3

Глава II……………………………………………………………………………….5

2.1 «Красивые» задачи по содержанию…………………………………………….5

2.2 «Красивые» задачи по чертежу…………………………………………….……6

2.3 «Красивые» задачи по решению……………………………………………..… 7

2.4 «Красивые» олимпиадные задачи…………………………………………… 8

2.3 «Красивые» экономические задачи…………………………………………..… 9

Заключение……………………………………………………………………….….10

Список используемой литературы……………………………………………..…11

ВВЕДЕНИЕ

Математика – один из моих любимых предметов, решение различных математических задач привлекало меня, начиная с начальных классов. Именно на уроках математики я столкнулась с выражением «красивые задачи». Возник вопрос: ««Красивые» задачи в математике – какие они?»

Четких формулировок и определений «красивой» математической задачи в изученной мною литературе не оказалось, поэтому возникла проблема

– какие математические задачи считать «красивыми», как определить грань между «красивой» задачей и задачей обычной?

Было принято решение провести исследование по возникшей проблеме, подготовить исследовательскую работу на школьную научно-практическую конференцию по теме: «Красивые» задачи в математике». Актуальность выбранной темы была подтверждена в ходе обсуждения ее с учителем математики, который одобрил выбор темы исследования. Действительно, дать определение «красивой» задачи, подобрать такие задачи, классифицировать их определенным образом и, возможно, создать сборник таких задач было очень заманчиво. Мы понимали, что такой сборник будет иметь и практическую значимость для учащихся и педагогов.

Были определены:

· Объектная область исследования - учебный предмет «математика»

· Объект исследования - решение математических задач

· Предмет исследования - математические задачи определенного типа.

Изучив научную литературу по данному вопросу, выдвигаем

гипотезу исследования – если окажется возможным из множества математических задач выбрать определенные («красивые») задачи и классифицировать их по некоторым признакам, то возможно создание сборника таких задач и использование его в качестве пособия для математического саморазвития.

Цель нашего исследования – создать сборник «красивых» математических задач.

Задачи:

1. Изучение научной литературы, научных публикаций по данной теме, анализ полученной информации.
2. Определение понятия «красивая» задача в математике.
3. Классификация найденных задач по разделам.
4. Создание сборника «красивых» математических задач.

Методы исследования:

1. Теоретические (анализ и синтез).
2. Эмпирические (сравнение).
3. Математические (статистические методы, метод визуализации данных).

Ожидаемые результаты:

1. Классификация «красивых» математических задач.
2. Сборник «красивых» задач по математике.
3. Использование созданного сборника учащимися гимназии при подготовке к олимпиадам, к урокам, для развития математических способностей.
4. Использование сборника учителями гимназии для организации работы с учащимися.

Глава I.

Красота» в математике

Человек немыслим без такого качества, как восприятие мира в его красоте и гармонии. Поэтому сегодня одним из основных направлений развития школы является поворот обучения к человеку, его ценностному потенциалу.

Многие из учащихся считают математику строгой наукой, при изучении которой нет места эмоциям, хотя очень многие заинтересованы этим предметом.

Известно, что решение задачи – одно из основных средств математического развития школьников. Каждая математическая задача служит конкретным целям обучения, но основная её цель – развитие творческого и математического мышления, формирование и развитие эстетического вкуса. Еще Д. фон Нейтман отмечал, что математика "движима почти исключительно эстетическими мотивами". Попытки раскрыть содержание понятий "чувство красоты", "красивая задача" предпринимаются многими математиками.

Например, Г. Биркгоф дал интересную характеристику эстетической привлекательности математического объекта: ,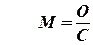

где М – мера красоты,

О – мера порядка,

С – мера усилий, затрачиваемых для понимания сущности объекта.

Из этой формулы следует, что для ученика красивыми математическими объектами будут те, восприятие которых сопряжено с наименьшими усилиями с его стороны. Эстетическая мера объекта будет увеличиваться с упорядочиванием структуры.

Многие планиметрические задачи напрямую связаны с понятием "красивая", то есть "доставляющая наслаждение, приятная внешним видом, гармоничностью, стройностью". Восприятие эстетической стороны такой задачи начинается с условия и чертежа.

Например, задача построения с помощью циркуля фигуры, изображенной на рисунке, 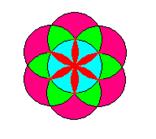привлекает внимание обучающихся прежде всего условием (красивый узор). Но затем они начинают фантазировать на данную тему, и у них получаются оригинальные узоры, построение которых возможно лишь с помощью циркуля.

Решение "красивых" задач, я считаю, должно быть наглядно, неожиданно, просто. Задачи, удовлетворяющие такому требованию, согласно моим наблюдениям, неизменно вызывают интерес учащихся и побуждают их к поиску более коротких и простых путей решения, что способствует развитию креативности.

Изучив множество литературы, я пришла к такому выводу, что «красивая» математическая задача должна отвечать определенным требованиям:

1) Условие задачи должно быть интересно; если задача геометрическая, то чертеж к ней красивый.

2) Задача должна содержать нестан­дартный элемент, отличающий ее от большинства задач по данной теме, предлагаемых в учебниках. При этом нестандартность может проявляться как в са­мом условии, так и в методах решения. Особый инте­рес в этом смысле представляют задачи, имеющие несколько различных методов решения, и многова­риантные задачи, имеющие несколько ответов (при­чем желательно, чтобы факт наличия нескольких ответов не был явно указан в формулировке условия).

3) Задача может устанавливать интересный факт, порой неожиданный.

4) 3адача должна быть доступна как по формулировке условия, так и по сложности и объе­му используемого в решении материала. Если силь­ные и слабые ученики окажутся при постановке про­блемы в изначально неравных условиях (чего во мно­гих случаях, к сожалению, не удается избежать), то предложенная задача потеряет долю своей прелести и «сработает» только на часть класса. Желательно, чтобы в решении красивой задачи не использовались искусственные приемы, особенно если они известны части учеников (например, посещающим занятия-кружка или факультатива).

5) Наконец, основное: в решении задачи обязательно нужно спрятать «изюминку», чтобы оно было наглядно и удивительно просто.

Учась в среднем звене и готовясь к математическим олимпиадам, я прорешала множество задач среди которых были такие, которые отвечали данным требованиям и я поняла, что их можно классифицировать на несколько групп:

1) «Красивые» задачи по решению; 2) «Красивые» задачи по чертежу;3) «Красивые» задачи по содержанию; 4) «Красивые» олимпиадные задачи; 5)«Красивые» экономические задачи.

Глава II

Красивые» задачи по содержанию

Некоторые «красивые» задачи привлекают учеников изюминкой, находящейся в содержании поставленной задачи. Приведу пример:

Маленький Петя подпилил все ножки у квадратного табурета и четыре отпиленных кусочка потерял. Оказалось, что длины всех кусочков различны и что табурет после этого стоит на полу, пусть наклонно, но по-прежнему касаясь, пола всеми четырьмя концами ножек. Дедушка решил починить табурет, однако нашел только три кусочка с длинами 8, 9 и 10 см. Какой длины может быть четвертый кусочек?

Решение. Пусть А, В, С, D – концы исходных ножек табуретки, а А¹, В¹, С¹, D¹ – подпиленных. А¹А + В¹В = С¹С + D¹D. Поскольку табуретка стоит, касаясь пола четырьмя ножками, то точки А¹, В¹, С¹ и D¹ лежат в одной плоскости. Табуретка квадратная, значит, плоскости АВА¹В¹ и СDС¹D¹ параллельны. Следовательно, А¹В^{1 //} С¹D¹. Аналогично,

В¹С¹ // А¹D¹. таким образом, четырехугольник А¹В¹С¹D¹ – параллелограмм, и его диагонали пересекаются в точке О¹. Пусть О – центр квадрата АВСD. Заметим, что отрезок ОО¹ – средняя линия как в трапеции АСС¹А¹, так и в трапеции ВDD¹В¹, а значит , А¹А+ С¹С= 2ОО¹= В¹В+ D¹D.

Теперь переберем возможные длины отпиленной части, расположенной по диагонали от потерянной. При этом получим, что длина отпиленной части удовлетворяет одному из равенств:

8+x=9+10, 9+x=8+10, 10+x=8+9, x=7, x=9,x=11.

Поскольку длины всех кусков различны, =9, и остаются только варианты 7 и 11.

Ответ: 7,11.