Критерий ожидаемого значения.

Теория игр и принятие решений.

В зависимости от условий внешней среды и степени информативности лица принимающего решение (ЛПР) производится следующая классификация задач принятия решений:

а) в условиях риска;

б) в условиях неопределённости;

в) в условиях конфликта или противодействия (активного противника).

Часть 1. Теория полезности и принятия решений.

Глава 1. Принятие решений в условиях риска.

Критерий ожидаемого значения.

Использование критерия ожидаемого значения обусловлено стремлением максимизировать ожидаемую прибыль (или минимизировать ожидаемые затраты). Использование ожидаемых величин предполагает возможность многократного решения одной и той же задачи, пока не будут получены достаточно точные расчётные формулы. Математически это выглядит так: пусть Х случайная величина с математическим ожиданием MX и дисперсией DX. Если x₁,x₂,...,x_n  значения случайной величины (с.в.) X, то среднее арифметическое их (выборочное среднее) значений 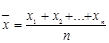имеет дисперсию 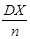. Таким образом, когда n ® ¥

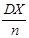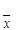® 0 и ® MX.

Другими словами при достаточно большом объёме выборки разница между средним арифметическим и математическим ожиданием стремится к нулю (так называемая предельная теорема теории вероятности). Следовательно, использование критерия ожидаемое значение справедливо только в случае, когда одно и тоже решение приходится применять достаточно большое число раз. Верно и обратное: ориентация на ожидания будет приводить к неверным результатам, для решений, которые приходится принимать небольшое число раз.

Пример 1. Требуется принять решение о том, когда необходимо проводить профилактический ремонт ПЭВМ, чтобы минимизировать потери из-за неисправности. В случае если ремонт будет производится слишком часто, затраты на обслуживание будут большими при малых потерях из-за случайных поломок.

Так как невозможно предсказать заранее, когда возникнет неисправность, необходимо найти вероятность того, что ПЭВМ выйдет из строя в период времени t. В этом и состоит элемент риска.

Математически это выглядит так: ПЭВМ ремонтируется индивидуально, если она остановилась из-за поломки. Через T интервалов времени выполняется профилактический ремонт всех n ПЭВМ. Необходимо определить оптимальное значение Т, при котором минимизируются общие затраты на ремонт неисправных ПЭВМ и проведение профилактического ремонта в расчёте на один интервал времени.

Пусть р_t  вероятность выхода из строя одной ПЭВМ в момент t, а n_t  случайная величина, равная числу всех вышедших из строя ПЭВМ в тот же момент. Пусть далее С₁  затраты на ремонт неисправной ПЭВМ и С₂  затраты на профилактический ремонт одной машины.

Применение критерия ожидаемого значения в данном случае оправдано, если ПЭВМ работают в течение большого периода времени. При этом ожидаемые затраты на один интервал составят

ОЗ = ,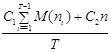

где M(n_t)  математическое ожидание числа вышедших из строя ПЭВМ в момент t. Так как n_t имеет биномиальное распределение с параметрами (n, p_t), то M(n_t) = np_t . Таким образом

ОЗ =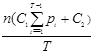

Необходимые условия оптимальности T^* имеют вид:

ОЗ (T^*-1) ³ ОЗ (T^*),

ОЗ (T^*+1) ³ ОЗ (T^*).

Следовательно, начиная с малого значения T, вычисляют ОЗ(T), пока не будут удовлетворены необходимые условия оптимальности.

Пусть С₁ = 100; С₂ = 10; n = 50. Значения p_t имеют вид:

T	рt		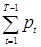ОЗ(Т)
	0.05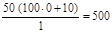
	0.07	0.05
	0.10	0.12	366.7
	0.13	0.22
	0.18	0.35

T^*® 3 , ОЗ(Т^*) ® 366.7

Следовательно профилактический ремонт необходимо делать через T^*=3 интервала времени.