Определение ускорения свободного падения

Лабораторная работа №3

Цель: Изучение динамики движения тел в поле гравитационного притяжения.

Задача: измерение ускорения свободного падения с помощью математического и физического маятников

Оборудование: универсальный маятник ФПМ-04

Рабочими являются формулы периода колебаний Т математического и физического маятников

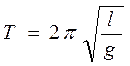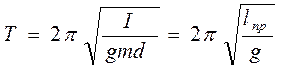(1) (2)

где l – длина математического маятника; m – масса, I – момент инерции, d– расстояние от точки подвеса до центра тяжести физического маятника; l_пр – приведенная длина физического маятника, которая равна длине математического маятника с таким же периодом колебаний.

Определив периоды колебаний математического и физического маятников, а также их геометрические параметры (длины), используя эти формулы, вычислим ускорение свободного падения g.

Описание экспериментальной установки:

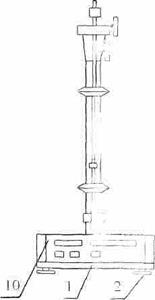
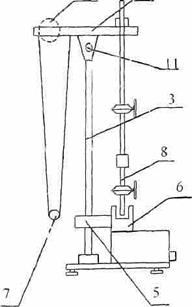Общий вид универсального маятника ФПМ-04 представлен на рис. 1. Основание (1) оснащено регулируемыми ножками (2), которое позволяют произвести выравнивание прибора. В основание закреплена колонка (3), на которой установлен верхний кронштейн (4) и нижний кронштейн (5) с фотоэлектрическим датчиком (6)

Рис. 1. Универсальный маятник ФПМ-04

Отворачивая вороток (11), можно поворачивать вокруг колонки верхний кронштейн. Затягиванием воротка (11) фиксируют кронштейн в любом произвольно выбранном положении.

С одной стороны кронштейна (4) находится математический маятник (7), на вмонтированных вкладышах оборотный маятник (8).

Длину маятника можно регулировать при помощи воротка (9)_, а ее величину можно определить при помощи шкалы на колонке (3).

Оборотный маятник выполнен в виде стального стержня, на котором зафиксированы два повернутых друг к другу лезвиями ножа и два ролика.

На стержне через 10 мм выполнены нарезки, служащие для точного определения длины оборотного маятника (расстояние между ножами). Ножи и ролики можно перемещать вдоль колонки и фиксировать в определенном избранном положении.

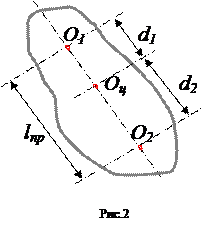Рассмотрим, чему равны периоды колебаний физического маятника при различном положении центров качания. (рис.2).

Пусть тело колеблется вокруг оси, проходящей через произвольно взятую точку О₁. Тогда эта точка будет называться центром (осью) вращения. Расстояние от оси вращения О₁ до центра тяжести O_ц равно d₁.

Момент инерции относительно оси О₁ по теореме Штейнера равен I₁ = I_o + md₁² (3)

где I_o - момент инерции относительно оси О_ц , проходящей через центр тяжести и параллельной оси вращения О_1. .

Период колебаний в этом случае будет:

; (4)

На линии, соединяющей точку О_1. и центр тяжести О_{ц. ,} выберем точку О₂ ниже центра тяжести на расстоянии d₂. При колебаниях вокруг этой новой оси вращения будем иметь период колебаний

; (5)

Изменяя расстояния d₁ и d₂, подберем их значения так, чтобы были одинаковые периоды колебаний. Т₁ = Т_2. Однако из этого условия с учетом (4) и (5) следует (см. приложение 2), что равенство возможно только при d₁ + d₂ = l_np

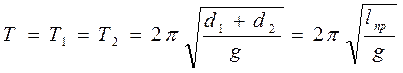(6)

Таким образом, при колебаниях вокруг оси вращения O₁ точка O₂ будет геометрическим положением для груза воображаемого математического маятника с таким же периодом колебаний, и называется центром качаний. Также для колебаний вокруг оси вращения O₂ точка O₁ обратно будет центром качаний.

При выполнении работы получение равенства периодов требует много времени и абсолютного равенства даже невозможно достичь. Поэтому надо просто постараться максимально приблизить Т₁ ≈ Т_2.

Из равенств имеем:

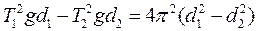; (7)

Выразим ускорение свободного падения:

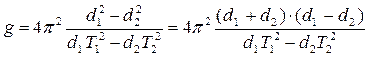; (8)

При достаточно близком равенстве Т₁ = Т₂ можно упростить расчетную формулу

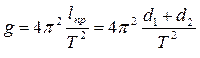(9)

Итак, для определения ускорения свободного падения необходимо определить период T относительно произвольной оси вращения, приведенную длину маятника l_пр как расстояние между двумя найденными соответствующими осями вращения с одинаковыми периодами качаний,.

Указания к выполнению работы:

Задание 1. Определитьg при помощи математического маятника:

• подготовить таблицу экспериментальных данных

№	l, м	tn- время колебаний, с	Δtn -- время n колебаний, с	Т - период колебаний, с	g – ускорение свободного падения, м/с2
Среднее значение g

· нижний кронштейн вместе с фотоэлектрическим датчиком
установить в нижней части колонки, обращая внимание на то,
чтобы верхняя грань кронштейна показывала на шкале длину
не меньше 50 см ( l = 50 см );

• затянуть вороток, фиксируя фотоэлектрический датчик в
избранном положении;

• поворачивая верхний кронштейн, установить длину
математического маятника, Обращая внимание на то, чтобы
черта на шарике (центр шарика) была продолжением черты на корпусе
фотоэлектрического датчика;

• привести математический маятник в движение, отклоняя
шарик на 4 - 5° от положения покоя.

• нажать кнопку «СБРОС»;

• после подсчета измерений времени колебаний (n = 10) нажать кнопку «СТОП»;

• определить период колебаний по формуле: 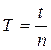, где t- продолжительность колебаний (общее время), п– количество полных колебаний;

• по шкале определить длину l маятника;

• по формуле 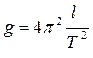определить g;

• заполнить соответствующие клетки в таблице

• измерения повторить 5 раз.

• Рассчитать среднее значение g

Задание 2 Определитьg при помощи оборотного маятника:

• подготовить таблицу экспериментальных данных

№	tn1-время колебаний на 1-м ноже	∆tn1	T1ср- период колебаний, с	tn2-время колебаний на 2-м ноже	∆tn2	T2ср- период колебаний, с
ср

· повернуть верхний кронштейн на 180°;

· укрепить ролики на стержне несимметрично, чтобы один из них находился на конце стержня, а другой на его середине;

· один нож закрепить вблизи свободного конца, а второй - на середине расстояния между роликами;

· проверить, совпадают ли грани лезвий с метками на стержне;

· закрепить маятник на ноже, находящемся вблизи конца стержня.

· нижний кронштейн вместе с фотоэлектрическим датчиком переместить так, чтобы стержень маятника пересекал оптическую ось;

· отклонить маятник на 4 -5° от положения равновесия и отпустить;

· нажать кнопку «СБРОС»;

· после подсчета измерителем времени колебаний (n = 5 колебаний) нажать кнопку «СТОП»:

· определить период колебаний по формуле: Т = t /п

· снять маятник и закрепить его на втором ноже;

· нижний кронштейн с фотоэлектрическим датчиком
переместить так, чтобы маятник пересекал оптическую ось;

· повторяя все операции с первым ножом, определить период
колебаний оборотного маятника Т₂ относительно второго
ножа;

· если Т₂> Т₁, то второй нож переместить в направлении ролика, находящегося в конце стержня, Если же Т₂ < Т₁, то переместить в направлении середины стержня, при этом размещение ролика и первого ножа не менять;

· изменять положение второго ножа до момента достижения равенства

Т₁ = Т₂ с точностью до 0,5%;

· определить приведенную длину оборотного маятника l_пр,

подсчитать количество нарезок на стержне между ножами;

· по формуле (8 или 9) определить ускорение свободного падения g;

Контрольные вопросы:

1. Что такое математический маятник?

2. Что такое физический маятник?

3. Что называется приведенной длиной физического маятника?

4. При каком расстоянии от центра масс до точки подвеса период колебаний маятника минимальный?

5. Как будет вести себя маятник, если совместить точку подвеса с центром масс?

6. Сформулируйте и докажите теорему Гюйгенса-Штейнера.

7. Выведите формулу периода колебаний физического маятника.

8. Как зависит g от высоты?

Литература:

1. Трофимова Т.И. Курс физики. М.: Высшая школа, 2007 г.

2. Матвеев А.Н.: Механика и теория относительности. – М., Высшая школа, 1986 г., стр. 219-228.

3. Лабораторный практикум по общей физике. Механика. Под ред. А.Н. Капитонова, Якутск, 1988г.

4. Габышев H.H. Методическое пособие по механике - Якутск.,ЯГУ, 1989

ПРИЛОЖЕНИЕ 1

МАССА – это количество вещества. m =ρV где ρ– плотность, V - объем. В классической механике масса – с одной стороны мера инертности и с другой - мера гравитационного взаимодействия.

Эти понятия вообще-то нетождественные, рассматривают разные условия проявления свойства массы. Вопрос такой: если некое тело притягивается Землей вдвое большей силой, чем второе тело, то при действии фиксированной силы первое тело должно двигаться с вдвое меньшим ускорением. Точные эксперименты показывают соответствие этих соотношений до 12-го знака.

Масса при релятивистских скоростях зависит от скорости, масса и энергия тела становятся прямо .связанными друг тс другом. Тесная связь массы и энергии наблюдается также в ядерных взаимодействиях.

СИЛА ТЯЖЕСТИ - следствие всемирного тяготения, т.е. проявления гравитационных свойств массы. Сила тяжести практически имеется везде >0, в любой точке Вселенной (в том числе и при невесомости!).

Для определения силы тяжести часто используются известные уравнения:

a mg

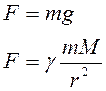
ВЕС - величина реакции опоры или подвеса. В условиях покоя или равномерного движения (инерциальные системы отсчета – ИСО) вес отождествляется с силой тяжести. В неинерциальных системах отсчета (НИСО) вес тела зависит от ускорения системы.

Так вес тела в лифте,

поднимающемся с ускорением абудет равно P=m (g+a)

опускающемся с ускорением абудет равно P=m (g - a)

Если нет опоры или подвеса, тело свободно падает, веса нет - невесомость.

На околоземной орбите спутник может вращаться достаточно долго (практически вакуум), описывает окружность, радиус закругления которой определяется нормальным (центростремительным) ускорением а_n, равным ускорению свободного падения.:

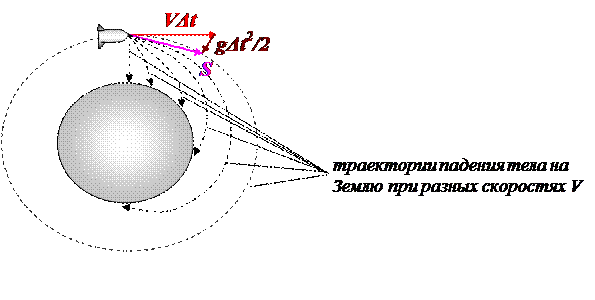
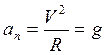
Таким образом, на орбите спутник неограниченно долго свободно падает на Землю, но все время мимо! (Земля слишком мала при таких скоростях).

ПРИЛОЖЕНИЕ 2

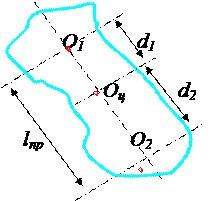
Момент инерции относительно оси О₁ по теореме Штейнера равен I₁ = I_o + md₁²

где I_o - момент инерции относительно оси О_ц , проходящей через центр тяжести и параллельной оси вращения О_1. .

Период колебаний в случае колебаний вокруг оси вращения О₁ будет:

; Период колебаний в случае колебаний вокруг оси вращения О₂ :

;

В случае равенства периодов колебаний Т₁ = Т_2. = Т имеем равенство

;

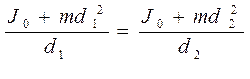Тогда J₀ ( d₂ – d₁) = m d₁ d₂(d₂– d₁);

Момент инерции вокруг центра тяжести будет J₀ = m d₁ d₂ ;

;

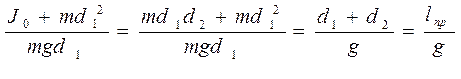или l_np = d₁ + d₂

Таким образом, для физического маятника, колеблющегося вокруг произвольной оси вращения O_{1 ,} можно найти на прямой, проходящей через O₁и центр тяжести O_{ц ,} дальше центра тяжести точку O_{2 ,} которая будет другой осью вращения с таким же периодом колебаний. Расстояние между этими точками O₁O₂ будет равно так называемой приведенной длине l_np физического маятника, которая есть длина математического маятника с таким же периодом колебаний.