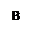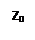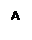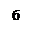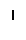Функция аргумента Arg(z)

Функция 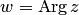является многозначной, что следует из способа введения полярных координат, а именно аргумент числа 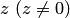определяется с точностью до слагаемого, кратного .

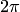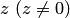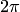При перемещении любой точки по произвольной непрерывной кривой аргумент числа непрерывно изменяется. При этом, если кривая замкнутая, то возможны два случая. В одном случае точка после обхода возвращается в исходное положение с прежним значением аргумента. Так будет для любой кривой, не совершающей обхода вокруг начала координат. В противном случае аргумент изменяется на величину или 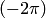в зависимости от направления обхода, а при n-кратном обходе — на 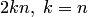или 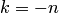. Это имеет месте в случае, когда точка при перемещении обходит начало координат.

Аргумент как функция точки будет однозначной функцией в области, которая не содержит кривых, совершающих обход точки 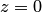. В качестве такой области можно взять плоскость с разрезом по любому лучу, выходящему из начала координат. В частности, с разрезом по действительной отрицательной полуоси — область 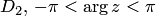. Можно выбрать разрез по действительной положительной полуоси — область 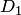, где главное значение аргумента определяется равенством 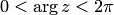. Заметим, что аргументы числа, геометрически соответствующего одной и той же точке областе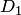й и 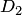, могут быть различны. 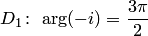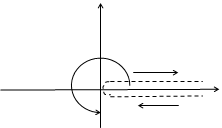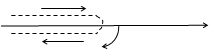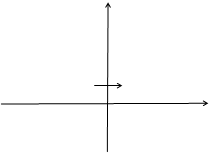Например, в области , а в области 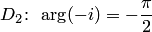(рис. 3.4).

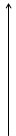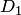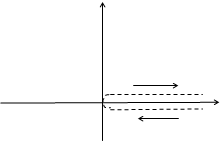
Границами каждой из областей и 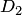являются два "берега" соответствующей полуоси, обход границ на рисунках указан стрелками.

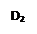
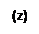
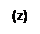
Пример 6. Исследовать возможность выделения однозначных ветвей неоднозначной, функции .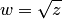

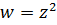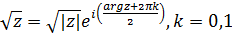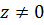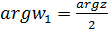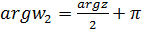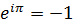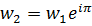Решение.Функция являетсянеоднозначной как обратная к неоднолистной функции . Ее неоднозначность (двузначность) связана с неоднозначностью аргумента функции . Для каждого значения получаем два значения аргумента: и . Так как и , то .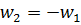

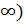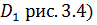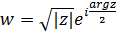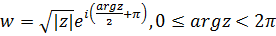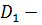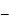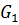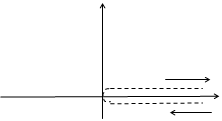
В комплексной плоскости с разрезом по лучу [0;+ ( возможно выделение однозначных ветвей аргумента. Можно рассмотреть две функции: и . Первая из них переводит область плоскость с разрезом в область , где 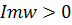( Рис. 3.5), так как для 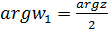имеем неравенство .

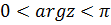Положительный обход границ указан стрелками. В точках границы области 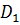однозначность нарушается, но в силу сделанного разреза действительные положительные значения (z=x, x>0) рассматриваются дважды на верхнем «берегу» и на нижнем «берегу». Например, при z=1 это точка 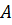верхнего «берега» и точка 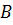нижнего «берега». При отображении 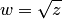точкам верхнего «берега» соответствуют положительные значения 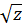(точка 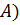, а точкам нижнего «берега» отрицательные значения (точка ).

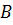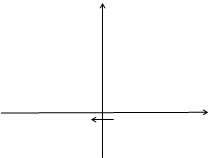
Вторая функция переводит область 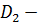плоскость с разрезом [0;+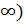 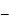в область 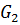, где 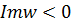( Рис. 3.6 ), так как для 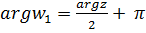имеем неравенство .

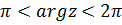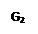
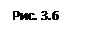
Граничным точкам верхнего «берега» соответствуют отрицательные значения функции 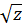(точка 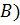, а точкам нижнего «берега» положительные значения (точка ).

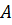Из приведенных рассуждений сформулируем следующее утверждение.

Двузначная функция 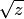отображает плоскость с разрезом по действительной положительной полуоси (область 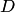) на верхнюю полуплоскости (область 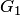) и нижнюю (область 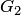). В области 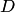возможно выделение однозначных ветвей — двух однозначных функций, одна из которых отображает 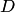на 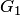, другая — 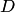на 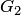. Однозначное отображение всей плоскости 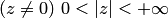невозможно.

Замечание. Проведение разреза в плоскости позволило получить однозначные функции, с которыми можно производить обычные операции

Если в плоскости 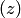точка описывает простую замкнутую кривую, обходя начало координат, то в плоскости 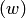ей будет соответствовать кривая, совершающая дважды обход вокруг .

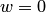Точка 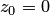, при обходе вокруг которой по замкнутой кривой точка переходит с одного листа на другой, называется точкой ветвления 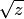. Также точкой ветвления 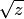является точка .

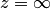Аналогично можно исследовать n-листную функцию 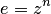и обратную к ней .

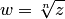Понятие предела

Число 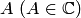называется пределом функции 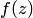в точке 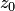, если для любого числа 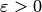найдется число 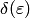такое, что для всех чисел , удовлетворяющих неравенству 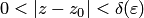, выполняется неравенство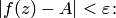

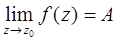
Геометрически это означает, что для точек из проколотой δ-окрестности точки 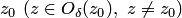соответствующие значения функции принадлежат ε-окрестности точки .

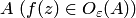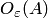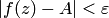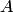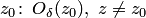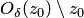Напомним, что окрестность точки на комплексной плоскости — это круг с центром в этой точке. Так, или есть круг радиуса с центром в точке , а проколотая окрестность точки или , или 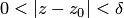— круг радиуса 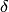с центром в точке 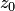за исключением точки .

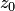Если записать числа в алгебраической форме, то нетрудно доказать справедливость следующего утверждения.

Утверждение.1(необходимое и достаточное условие существования предела функции комплексного переменного).

Для того чтобы в точке 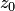существовал предел функции 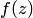, необходимо и достаточно, чтобы в точке 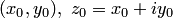существовали пределы двух функций действительных переменных 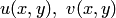, где 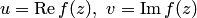; при этом имеет место равенство

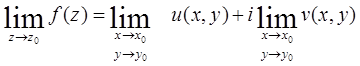
Замечания: 1. Из сформулированного критерия следует, что в комплексной области имеют место правила и свойства пределов такие же, как и в действительной области (за исключением, разумеется, свойств, связанных со знаками неравенств).

Например, 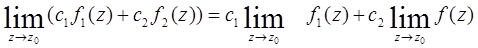(при условии, что существуют пределы в правой части равенства).

2. Можно определить понятие предела функции в точке, рассматривая не всю окрестность этой точки, а только некоторое связное множество точек из этой окрестности — предельный переход по множеству:

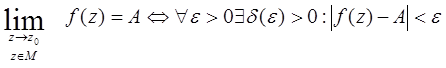
для .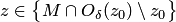

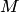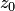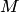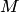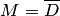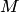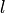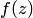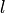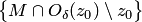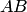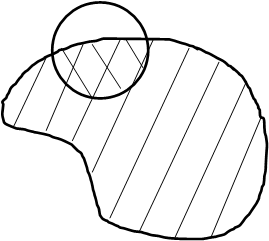
Здесь точки принадлежат пересечению множества и проколотой окрестности точки . В частности, это имеет место, если — множество точек кривой, или — замкнутое множество . Так, на рис. 3.7,а множество — кривая линия ,. Функция определена на и — дута , за исключением точки 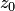. На рис. 3.7,б множество 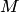— множество 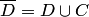, функция определена в област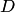и (или 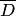), 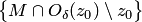— заштрихованная часть области .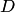
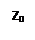