Обыкновенные дифференциальные уравнения

§1. Обыкновенные дифференциальные уравнения. Основные понятия. Задача Коши

1.1. Основные понятия и определения. Общее и частное решение.

1.2. Задача Коши. Теорема о существовании и единственности.

1.3. Типы уравнений 1-го порядка интегрируемые в квадратурах

1.4. Уравнения с разделенными и разделяющимися переменными.

1.5. Однородные дифференциальные уравнения первого порядка.

1.6. Линейные уравнения первого порядка.

1.7. Уравнение Бернулли.

§2. Дифференциальные уравнения высших порядков

2.1. Дифференциальные уравнения n-го порядка.

2.2. Типы дифференциальных уравнений разрешаемые в квадратурах.

2.3. Дифференциальные уравнения второго порядка, приводимые к уравнениям первого порядка (допускающие понижение порядка).

2.4. Дифференциальные уравнения высших порядков допускающие понижение порядка.

Линейные уравнения высших порядков. Структура общего решения

3.1. Линейные однородные дифференциальные уравнения n-го порядка с произвольными коэффициентами. Структура общего решения ЛОДУ.

3.2. Линейная зависимость функций. Определитель Вронского. Необходимое условие линейной зависимости и независимости решений ЛОДУ.

3.3. Неоднородные линейные уравнения высших порядков. Структура общего решения.

3.4. Метод вариации произвольных постоянных (метод Лагранжа).

3.5. Линейные однородные уравнения n-го порядка с постоянными коэффициентами.

3.6. Неоднородные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью.

Система обыкновенных дифференциальных уравнений

4.1. Основные понятия и определения.

4.2. Приведение нормальной системы дифференциальных уравнений к одному уравнению (метод исключения).

4.3. Интегрирование линейной системы с постоянными коэффициентами. Метод Эйлера. Характеристическое уравнение (случай простого спектра).

Числовые ряды

§1. Основные понятия и теоремы

1.1. Числовой ряд. Сумма, сходимость ряда.

1.2. Необходимый признак сходимости любых числовых рядов.

1.3. Простейшие свойства сходящихся рядов.

§2. Сходимость рядов с положительными членами.

2.1. Сравнение рядов с положительными членами. Признаки сравнения.

2.2. Достаточные признаки сходимости для знакоположительных рядов: признак Д’Аламбера, радикальный признак Коши, интегральный признак сходимости Маклорена-Коши.

Знакопеременные числовые ряды

§1. Знакочередующиеся ряды. Теорема Лейбница

§2. Знакопеременные ряды. Абсолютная и условная сходимость

.

Степенные ряды

§1. Степенные ряды. Теорема Абеля. Интервал сходимости и методы его определения.

§2. Дифференцирование и интегрирование степенных рядов.

§3. Ряды по степеням (x–a).

§4. Ряды Тейлора и Маклорена.

§5. Разложение элементарных функций: 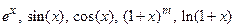, 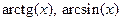в

ряд Маклорена.

§6. Использование степенных рядов в приближенных вычислениях (функций и интегралов).