Перемещение и скорость
1) В верхнем левом углу расположена стрелка. Нажмите на стрелку, перейдите к лабораторной работе № 1.2. Перед Вами график зависимости координаты от времени движения автомобиля, а так же автомобиль.
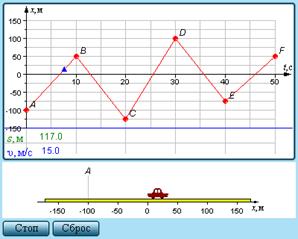
2) Нажмите «Старт». Автомобиль начинает двигаться. Под графиком приведены значения перемещения и скорости на каждом участке движения автомобиля.
3) Вид графика может меняться. Подведите стрелку мыши к той точке графика, которую Вы хотите передвинуть. Нажмите левую кнопку мыши и перенесите точку туда, куда необходимо. Отпустите кнопку. Нажмите «Старт», пронаблюдайте движения автомобиля.
4) Повторите моделирование необходимое количество раз (по указанию преподавателя).
5) Зарисуйте рисунок в тетрадь, запишите полученные результаты, либо распечатайте результат на принтере.
6) Ответьте на вопросы и решите задачи, расположенные в правой половине экрана.
7) Кликните мышью «Журнал». Обнулите результаты в таблице, нажав кнопку «Сброс результатов».
8) Проведите минитестирование. Ответьте на вопросы из раздела «Вопросы» и решите задачи из раздела «Задачи». Результат сообщите преподавателю.
9) Дома проработайте модель 1.4 из раздела «Модели».
10) Напишите вывод.
3. Контрольные вопросы
1. Перечислите и дайте определения основных разделов механики.
2. Модели в механике.
3. Что называется телом отсчета, системой отсчета?
4. Дайте определения траектории, длины пути, вектора перемещения.
5. Какое движение называется поступательным?
6. Дайте определение средней и мгновенной скоростей.
7. Ускорение и его (тангенциальная и нормальная) составляющие.
8. Относительные величины.
9. Закон сложения скоростей.
10. Какое движение называется равномерным?
11. Закон движения при равномерном прямолинейном движении.
Лабораторная работа № 2
Движение тел с ускорением.
Равноускоренное движение. Скорость и ускорение.
Свободное падение тела
Цель работы: изучение равноускоренного движения, понятий скорость и ускорение, свободного падения тел, моделей.
Краткая теория
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения 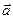 остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения
остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения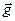 . Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т.е. вдоль оси OX (рис. 1.1).
. Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т.е. вдоль оси OX (рис. 1.1).
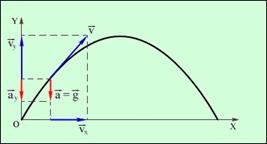 Рис. 1.1. Проекции векторов скорости Рис. 1.1. Проекции векторов скорости 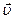 и ускорения и ускорения 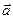 на координатные оси. ax=0, ay=–g. на координатные оси. ax=0, ay=–g. | Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости 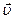 и ускорения и ускорения 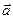 направлены вдоль прямой движения. Поэтому скорость υ и ускорение a можно рассматривать в проекциях на направление движения как алгебраические величины. направлены вдоль прямой движения. Поэтому скорость υ и ускорение a можно рассматривать в проекциях на направление движения как алгебраические величины. |
При равноускоренном прямолинейном движении скорость тела определяется формулой
| υ=υ0+at. | (1.1) |
В этой формуле υ0 – скорость тела при t=0 (начальная скорость), a=const – ускорение. На графике скорости υ(t) эта зависимость изображается прямой линией (рис. 1.2).
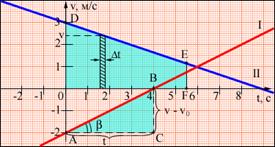 Рис. 1.2. Графики скорости равноускоренного движения. Рис. 1.2. Графики скорости равноускоренного движения. | По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.2 для графика I. Ускорение численно равно отношению сторон треугольника АВС: 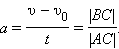 |
Чем больше угол β, который образует график скорости с осью времени, т.е. чем больше наклон графика (крутизна), тем больше ускорение тела.
Для графика I: υ0 = –2 м/с, a = 1/2 м/с2.
Для графика II: υ0 = 3 м/с, a = –1/3 м/с2.
Изучите модель «Скорость и ускорение».
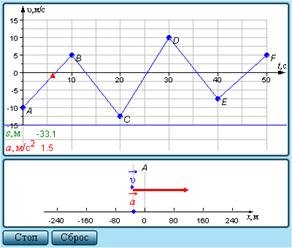 | Модель демонстрирует графики движения тела с постоянным ускорением. График υ состоит из отрезков прямых. Его можно менять с помощью мыши. При движении тела для каждого прямолинейного участка вычисляется величина ускорения a и перемещения s. |
| Модель. Скорость и ускорение. |
График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т.е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной на рис. 1.2 полоски. Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, можно получить, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены на рис. 1.2 для графика II. Время t принято равным 5,5 с.
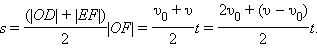 |
Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:
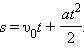 | (1.2) |
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:
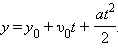 | (1.3) |
Это выражение называют законом равноускоренного движения.
Изучите модель «Графики равноускоренного движения».
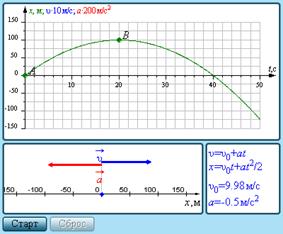 | Модель демонстрирует графики равноускоренного движения. График x(t), представляющий собой параболу, можно менять с помощью мыши. После команды «Старт» движущаяся точка на графике x(t) демонстрирует движение тела; при этом одновременно рисуются графики скорости υ(t) и ускорения a(t). |
| Модель. Графики равноускоренного движения. |
При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений (1.1) и (1.2) путем исключения из них времени t. Результат записывается в виде
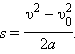 | (1.4) |
Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и перемещение s:
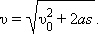 | (1.5) |
Если начальная скорость υ0 равна нулю, эти формулы принимают вид
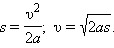 | (1.6) |
Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ0, υ, s, a, y0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.
В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения 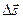 При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.2).
При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.2).
Изучите модель «Равноускоренное движение тела».
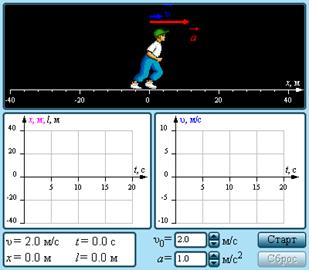 | Модель демонстрирует равноускоренное движение бегуна. Выбрав величины начальной скорости и ускорения бегуна (это можно сделать как с помощью соответствующих окон ввода, так и непосредственно на графике с помощью мыши), наблюдайте за изменением во времени координаты x, пройденного пути l и скорости υ. Проследите за движением бегуна в случае, когда начальная скорость и ускорение имеют разные знаки. |
| Модель. Равноускоренное движение тела. |
Свободным падением тел называют падение тел на Землю в отсутствие сопротивления воздуха (в пустоте). В конце XVI века знаменитый итальянский ученый Г. Галилей опытным путем установил с доступной для того времени точностью, что в отсутствие сопротивления воздуха все тела падают на Землю равноускоренно, и что в данной точке Земли ускорение всех тел при падении одно и то же. До этого в течение почти двух тысяч лет, начиная с Аристотеля, в науке было принято считать, что тяжелые тела падают на Землю быстрее легких.
Ускорение, с которым падают на Землю тела, называется ускорением свободного падения. Вектор ускорения свободного падения обозначается символом 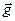 он направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение g оказывается неодинаковым, изменяясь примерно от 9,83 м/с2 на полюсах до 9,78 м/с2 на экваторе. На широте Москвы g = 9,81523 м/с2. Обычно, если в расчетах не требуется высокая точность, то принимают числовое значение g у поверхности Земли равным 9,8 м/с2 или даже 10 м/с2.
он направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение g оказывается неодинаковым, изменяясь примерно от 9,83 м/с2 на полюсах до 9,78 м/с2 на экваторе. На широте Москвы g = 9,81523 м/с2. Обычно, если в расчетах не требуется высокая точность, то принимают числовое значение g у поверхности Земли равным 9,8 м/с2 или даже 10 м/с2.
Простым примером свободного падения является падение тела с некоторой высоты h без начальной скорости. Свободное падение является прямолинейным движением с постоянным ускорением. Если направить координатную ось OY вертикально вверх, совместив начало координат с поверхностью Земли, то для анализа свободного падения без начальной скорости можно использовать формулу (1.3), положив υ0 = 0, y0 = h, a = –g. Обратим внимание на то, что если тело при падении оказалось в точке с координатой y < h, то перемещение s тела равно s = y – h < 0. Эта величина отрицательна, так как тело при падении перемещалось навстречу выбранному положительному направлению оси OY. В результате получим:
| υ = –gt. | (1.7) |
Скорость отрицательна, так как вектор скорости направлен вниз.
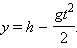 | (1.8) |
Время падения tn тела на Землю найдется из условия y = 0:
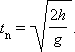 | (1.9) |
Скорость тела в любой точке составляет:
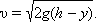 | (1.10) |
В частности, при y = 0 скорость υn падения тела на землю равна
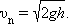 | (1.11) |
Пользуясь этими формулами, можно вычислить время падения тела с данной высоты, скорость падения тела в любой момент после начала падения и в любой точке его траектории и т. д.
Аналогичным образом решается задача о движении тела, брошенного вертикально вверх с некоторой начальной скоростью υ0. Если ось OY по-прежнему направлена вертикально вверх, а ее начало совмещено с точкой бросания, то в формулах равноускоренного прямолинейного движения следует положить: y0 = 0, υ0 > 0, a = –g. Это дает:
| υ = υ0 – gt. | (1.12) |
Через время υ0 /g скорость тела υ обращается в нуль, т.е. тело достигает высшей точки подъема. Зависимость координаты y от времени t выражается формулой
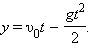 | (1.13) |
Тело возвращается на землю (y = 0) через время 2υ0 / g, следовательно, время подъема и время падения одинаковы. Во время падения на землю скорость тела равна –υ0, т.е. тело падает на землю с такой же по модулю скоростью, с какой оно было брошено вверх.
Максимальная высота подъема
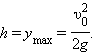 | (1.14) |
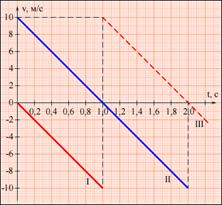 Рис. 1.3. Графики скоростей для различных режимов движения тела с ускорением a = –g. Рис. 1.3. Графики скоростей для различных режимов движения тела с ускорением a = –g. | На рис. 1.3 представлены графики скоростей для трех случаев движения тела с ускорением a = –g. График I соответствует случаю свободного падения тела без начальной скорости с некоторой высоты h. Падение происходило в течение времени tn = 1 с. Из формул для свободного падения легко получить: h = 5 м (все цифры в этих примерах округлены, ускорение свободного падения принято равным g = 10 м/с2). График II – случай движения тела, брошенного вертикально вверх с начальной скоростью υ0 = 10 м/с. |
Максимальная высота подъема h = 5 м. Тело возвращается на землю через время 2 секунды.
График III – продолжение графика I. Свободно падающее тело при ударе о землю отскакивает (мячик), и его скорость за очень короткое время меняет знак на противоположный. Дальнейшее движение тела не отличается от случая II.
Задача о свободном падении тел тесно связана с задачей о движении тела, брошенного под некоторым углом к горизонту. Для кинематического описания движения тела удобно одну из осей системы координат направить вертикально вверх (ось OY), а другую (ось OX) - расположить горизонтально. Тогда движение тела по криволинейной траектории можно представить как сумму двух движений, протекающих независимо друг от друга – движения с ускорением свободного падения вдоль оси OY и равномерного прямолинейного движения вдоль оси OX. На рис. 1.4 изображен вектор начальной скорости 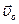 тела и его проекции на координатные оси.
тела и его проекции на координатные оси.
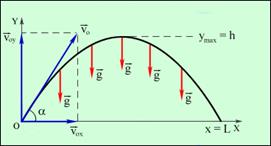 Рис. 1.4. Движение тела, брошенного под углом Рис. 1.4. Движение тела, брошенного под углом 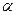 к горизонту. Разложение вектора к горизонту. Разложение вектора 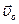 начальной скорости тела по координатным осям. начальной скорости тела по координатным осям. | Таким образом, для движения вдоль оси OX имеем следующие условия: x0 = 0, υox = υ0 cos α, ax = 0, а для движения вдоль оси OY y0 = 0, υoy = υ0 sin α, ay = –g. Приведем здесь некоторые формулы, описывающие движение тела, брошенного под углом α к горизонту. Время полета: | ||||
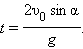 | (1.15) | ||||
Дальность полета:
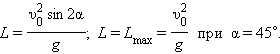 | (1.16) |
Максимальная высота подъема:
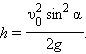 | (1.17) |
Изучите модель «Движение тела, брошенного под углом к горизонту».
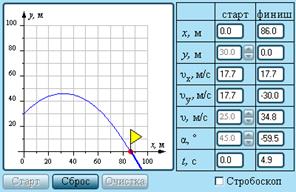 Модель. Движение тела, брошенного под углом к горизонту. Модель. Движение тела, брошенного под углом к горизонту. | Модель демонстрирует движение тела, брошенного под углом к горизонту. Можно изменять начальную высоту, а также модуль и направление скорости тела. В режиме «Стробоскоп» на траектории через равные промежутки времени показываются вектор скорости брошенного тела и его проекции на горизонтальную и вертикальную оси. Определите в компьютерном эксперименте, при каком угле бросания при начальной высоте y = 0 и при заданной начальной скорости дальность полета максимальна. |
Движение тела, брошенного под углом к горизонту, происходит по параболической траектории. В реальных условиях такое движение может быть в значительной степени искажено из-за сопротивления воздуха, которое может во много раз уменьшить дальность полета тела.
