Методика и порядок выполнения работы. 5.1Прогнозирование произвести на примере спроса на деталь (таблица 6.1).

5.1Прогнозирование произвести на примере спроса на деталь (таблица 6.1).

Таблица 6.1 – Оценка спроса на деталь экспертами.

№ варианта	№ эксперта	Оценка в баллах спроса на деталь

5.2 В качестве наглядного примера рассмотрим вариант №1.

5.3 Оценка важности параметров в баллах изложена ниже.

При оценке важности параметров в баллах каждый эксперт оценивает параметры по десятибалльной системе. При этом оценка, назначаемая каждым экспертом каждому параметру, не связана с оценками, которые он же назначает другим параметрам. Например, всем параметрам можно назначить одинаковую оценку.

5.4 Сформировать таблицу по форме, представленной на рисунке 6.2, в которую вносятся оценки всех параметров в баллах, сделанные каждым экспертом.

Рисунок 6.2 – Исходные данные

В ячейках F4:F7 введены функции суммирования.

5.5 Сделать таблицу по форме, представленной на рисунке 6.3, которая будет базовой.

Рисунок 6.3 – Базовая таблица

5.6 Ввести функции Excel, определяющие среднее значение, среднее квадратическое отклонение, дисперсию, как это показано в ячейках С8:Е10. Введённые в ячейки В4:Е7 формулы обеспечивают переход от оценок параметров в баллах к значениям коэффициентов веса, сумма которых для всех параметров равна единице у каждого эксперта.

5.7 В ячейки С11:Е11 ввести формулы для определения коэффициента вариабельности.

Значение коэффициента вариабельности показывает величину разброса экспертных оценок. При V 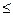0,2 оценки экспертов можно считать согласованными. В случае V 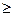0,2 целесообразно провести с экспертами содержательное обсуждение важности оцениваемых параметров, после чего повторить экспертизу.

5.8 Для прогноза с помощью метода экспертного опроса составим ряд вероятностного спроса на запасную часть. Такой ряд можно получить с помощью системы STATISTICA в среде WINDOWS. Для этого в меню системы существует панель Probability Distribution Calculator.(рисунок 6.4)

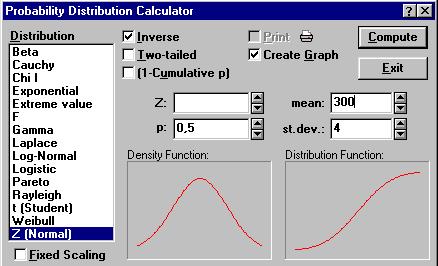
Рисунок 6.4 – Панель Вероятностный калькулятор

5.9 Выбрать нормальный закон распределения и вводя среднее значение прогноза и среднее квадратическое отклонение прогноза, получаем кривую плотности распределения (рисунок 6.5)

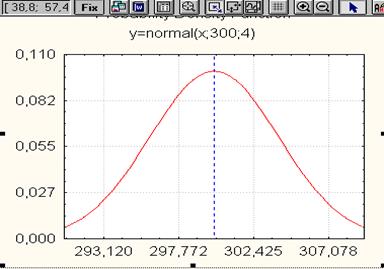
Рисунок 6.5 – Кривая плотности распределения

Значение функции распределения выдаётся в верхнем левом углу рисунка.

Ряд вероятностного спроса на деталь для полученного среднего значения – 347 шт. и среднего квадратического отклонения – 4 представлен на рисунке 6.6.

В качестве экспертов были привлечены пять менеджеров по снабжению из автотранспортных предприятий и станций технического обслуживания автомобилей. Наиболее предпочтительный вариант оценивался ими 10 баллами, а наименее предпочтительный – 1 баллом.

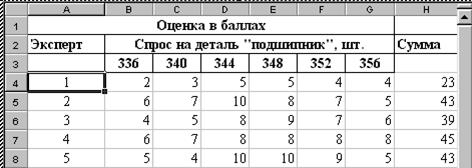
Рисунок 6.6 – Результаты опроса экспертов о прогнозном спросе на деталь «подшипник»

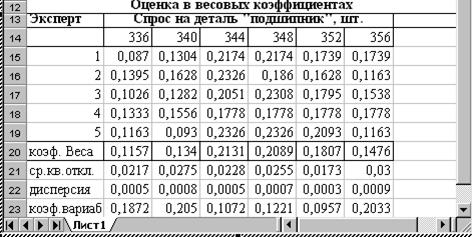
Рисунок 6.7 – Оценка в весовых коэффициентах

5.10 Произведённые расчёты свидетельствуют о том, что прогнозное значение спроса на деталь «подшипник», полученное с помощью эвристического прогноза, составит 344 шт.

Содержание отчета и его форма

Отчет должен содержать:

6.1 Исходные данные.

6.2 Расчет средних значений.

6.3 Расчет средних квадратических отклонений.

6.4 Расчет дисперсий.

6.5 Расчет коэффициентов вариабельности.

6.6 Расчет коэффициентов веса.

6.7 Выводы.

Контрольные вопросы и защита работы

7.1 На чем основан метод прогнозирования?

7.2 Каковы достоинства метода?

7.3 Каковы недостатки метода?

7.4 Изложить алгоритм получения экспертных оценок?

7.5 Изложить механизм формирования группы экспертов?

7.6 Как определяется оптимальное число экспертов?

7.7 Какие этапы включает в себя обработка данных экспертного прогноза?

Защита работы проводится в устной форме, состоит в предоставлении студентом правильно выполненного отчета по работе, коротком докладе и в ответах на вопросы, представленные выше.