Транспортная задача открытого типа
Если суммарные мощности поставщиков 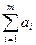 не равны суммарным потребностям потребителей
не равны суммарным потребностям потребителей 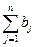 , то задача называется транспортной задачей открытого типа.
, то задача называется транспортной задачей открытого типа.
Транспортную задачу открытого типа нетрудно преобразовать в задачу закрытого типа. Пусть, например, в транспортной задаче открытого типа суммарный объем запасов превышает суммарный объем потребностей, то есть:
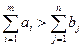 .
.
Введем «фиктивного» потребителя 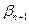 , и его потребности определим следующим образом:
, и его потребности определим следующим образом:
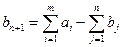
Коэффициенты затрат в столбце, соответствующем «фиктивному» потребителю, возьмем равными нулю.
Таким образом, получается транспортная задача закрытого типа, которая решается обычным методом.
Если же в транспортной задаче суммарный объем потребностей превышает суммарный объем запасов: 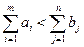 , в этом случае вводится аналогично «фиктивный» поставщик и задача открытого типа сводится к задаче закрытого типа.
, в этом случае вводится аналогично «фиктивный» поставщик и задача открытого типа сводится к задаче закрытого типа.
Замечание:
Метод потенциалов можно применить лишь в том случае, если при нахождении первого опорного решения, на каждом шаге заполнения таблицы поставок из рассмотрения выпадает либо строка (мощности соответствующего поставщика реализованы), либо столбец (запросы соответствующего потребителя удовлетворены), и только на последнем шаге одновременно выпадают и строка, и столбец. В этом случае число заполненных клеток (базисных переменных) на каждом шаге равно 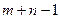 . Если при нахождении первого опорного решения, на каком-либо шаге, отличном от последнего, выпали одновременно строка и столбец , то для того, чтобы в дальнейшем можно было применить метод потенциалов, рекомендуется дать нулевую поставку в любую пустую клетку выпадающей строки или выпадающего столбца.
. Если при нахождении первого опорного решения, на каком-либо шаге, отличном от последнего, выпали одновременно строка и столбец , то для того, чтобы в дальнейшем можно было применить метод потенциалов, рекомендуется дать нулевую поставку в любую пустую клетку выпадающей строки или выпадающего столбца.
Задача №5.2.
Условие транспортной задачи задано распределительной таблицей.
| поставщики | потребители | запасы | ||
 | 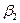 | 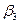 | ||
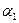 | ||||
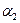 | ||||
 | ||||
| потребности |
Найти оптимальное распределение поставок и минимальные затраты на перевозку груза, выполнив первоначальное распределение методом наименьших затрат.
Решение.
Данная задача является задачей открытого типа: суммарные мощности поставщиков превышают на 30 единиц суммарные потребности потребителей. Введем «фиктивного потребителя» 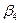 , присвоив соответствующим клеткам распределительной таблицы нулевые коэффициенты затрат.
, присвоив соответствующим клеткам распределительной таблицы нулевые коэффициенты затрат.
| поставщики | потребители | запасы | |||
 |  | 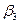 | 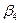 | ||
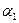 | |||||
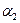 | |||||
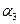 | |||||
| потребности |
Первое опорное решение найдем методом наименьших затрат. В одну из трех клеток с нулевым коэффициентом затрат дадим максимально возможную поставку. Например, в клетку (2,4) дадим 30 единиц груза. Мощности второго поставщика будут реализована полностью, потребность четвертого потребителя полностью удовлетворена. Из рассмотрения одновременно выпадают вторая строка и четвертый столбец. Для того, чтобы в дальнейшем можно было воспользоваться критерием оптимальности, необходимо заполнить нулевой поставкой одну из клеток либо второй строки, либо четвертого столбца. Например, в клетку (2,2) дадим нулевую поставку 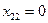 .
.
Следующую поставку дадим в клетку (1,3): 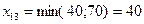 ; затем в клетку (1,2):
; затем в клетку (1,2): 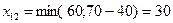 ; в клетку (3,1):
; в клетку (3,1): 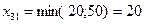 ; в клетку (3,2):
; в клетку (3,2): 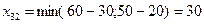 .
.
| поставщики | потребители | запасы | |||
 | 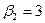 | 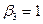 | 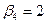 | ||
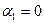 | 0 | 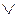 2 2 | |||
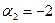 | -2 |   1 + 1 + | -1 |  0 - 0 - | |
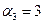 |  - 30 - 30 | 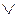 4 4 | 0 + 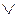 5 5 | ||
| потребности |
Полученный опорный план проверим на оптимальность. Обнулив 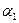 , вычислим остальные потенциалы. В свободные клетки внесем сумму потенциалов.
, вычислим остальные потенциалы. В свободные клетки внесем сумму потенциалов.
В клетках (3,1); (3,3) и (3,4) сумма потенциалов больше соответствующего коэффициента затрат, следовательно, построенный опорный план не является оптимальным.
Для клетки (3.4) построим замкнутый цикл перераспределения поставок.
Среди отрицательных вершин цикла выберем клетку с наименьшей по величине поставкой 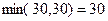 . Заметим, что при перераспределении 30 единиц груза по циклу одновременно обнулятся поставки в клетках (3,2) и (2,4):
. Заметим, что при перераспределении 30 единиц груза по циклу одновременно обнулятся поставки в клетках (3,2) и (2,4): 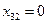 и
и 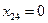 . Одну из переменных
. Одну из переменных 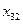 или
или 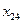 выведем из базиса, вводя в базис свободную переменную
выведем из базиса, вводя в базис свободную переменную 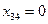 , а другую оставим в качестве базисной переменной. Например, оставим в базисе переменную
, а другую оставим в качестве базисной переменной. Например, оставим в базисе переменную 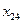 , заполнив клетку (2,4) нулевой поставкой.
, заполнив клетку (2,4) нулевой поставкой.
Полученный опорный план не будет оптимальным, так как в клетке (3,3) не выполняется критерий 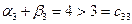 .
.
| поставщики | потребители | запасы | |||
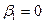 | 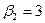 | 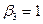 | 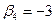 | ||
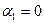 | 0 |   3 + 3 + |  1 - 1 - | -3 | |
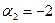 | -2 | -1 | |||
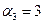 | 6 -  0 0 | 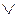 + 4 + 4 | |||
| потребности |
Выполним еще раз перераспределение груза по построенному циклу. Получим новое опорное решение, убедимся в выполнимости критерия оптимальности.
| поставщики | потребители | запасы | |||
 |  |  | 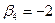 | ||
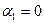 | 1 | -2 | |||
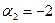 | -1 | -1 | -4 | ||
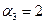 | 5 | ||||
| потребности |
Общая стоимость всех перевозок для данного плана будет наименьшей из всех возможных: 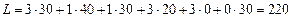 .
.
Ответ. Оптимальный план транспортировки груза:
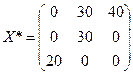 ,
,
при котором транспортные расходы по доставке груза всем трем пуктам потребления будут равны 220. У третьего поставщика после оптимального распределения поставок останутся не реализоваными 30 единиц груза.
