Лекция 9. Генераторы случайных чисел

В основе метода Монте-Карло (см. Лекцию 8. Статистическое моделирование) лежит генерация случайных чисел, которые должны быть равномерно распределены в интервале (0; 1).

Если генератор выдает числа, смещенные в какую-то часть интервала (одни числа выпадают чаще других), то результат решения задачи, решаемой статистическим методом, может оказаться неверным. Поэтому проблема использования хорошего генератора действительно случайных и действительно равномерно распределенных чисел стоит очень остро.

Математическое ожидание 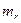и дисперсия 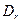такой последовательности, состоящей из 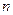случайных чисел 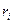, должны быть следующими (если это действительно равномерно распределенные случайные числа в интервале от 0 до 1):

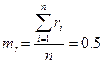
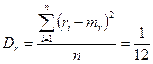
Если пользователю потребуется, чтобы случайное число x находилось в интервале (a; b), отличном от (0; 1), нужно воспользоваться формулой x = a + (b – a) · r, где r — случайное число из интервала (0; 1). Законность данного преобразования демонстрируется на рис. 9.1.

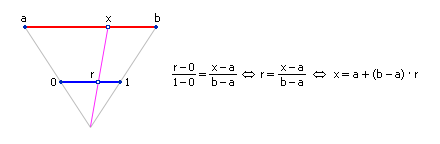
Рис. 9.1. Схема перевода числа из интервала (0; 1) в интервал (a; b)

Теперь x — случайное число, равномерно распределенное в диапазоне от a до b.

За эталон генератора случайных чисел (ГСЧ) принят такой генератор, который порождает последовательность случайных чисел с равномерным законом распределения в интервале (0; 1). За одно обращение данный генератор возвращает одно случайное число. Если наблюдать такой ГСЧ достаточно длительное время, то окажется, что, например, в каждый из десяти интервалов (0; 0.1), (0.1; 0.2), (0.2; 0.3), …, (0.9; 1) попадет практически одинаковое количество случайных чисел — то есть они будут распределены равномерно по всему интервалу (0; 1). Если изобразить на графике k = 10 интервалов и частоты N_i попаданий в них, то получится экспериментальная кривая плотности распределения случайных чисел (см. рис. 9.2).

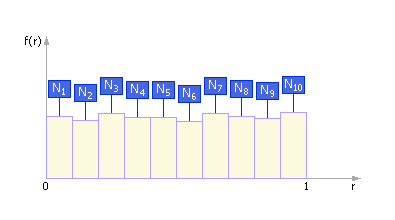
Рис. 9.2. Частотная диаграмма выпадения случайных чисел,
порождаемых реальным генератором

Заметим, что в идеале кривая плотности распределения случайных чисел выглядела бы так, как показано на рис. 9.3. То есть в идеальном случае в каждый интервал попадает одинаковое число точек: N_i = N/k, где N — общее число точек, k — количество интервалов, i = 1, …, k.

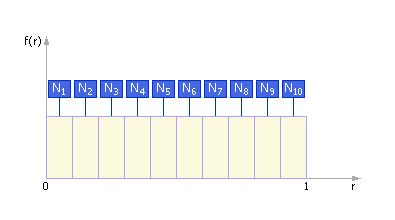
Рис. 9.3. Частотная диаграмма выпадения случайных чисел,
порождаемых идеальным генератором теоретически

Следует помнить, что генерация произвольного случайного числа состоит из двух этапов:

• генерация нормализованного случайного числа (то есть равномерно распределенного от 0 до 1);
• преобразование нормализованных случайных чисел r_i в случайные числа x_i, которые распределены по необходимому пользователю (произвольному) закону распределения или в необходимом интервале.

Генераторы случайных чисел по способу получения чисел делятся на:

• физические;
• табличные;
• алгоритмические.

Физические ГСЧ

Примером физических ГСЧ могут служить: монета («орел» — 1, «решка» — 0); игральные кости; поделенный на секторы с цифрами барабан со стрелкой; аппаратурный генератор шума (ГШ), в качестве которого используют шумящее тепловое устройство, например, транзистор (рис. 9.4–9.5).

Рис. 9.4. Схема аппаратного метода генерации случайных чисел

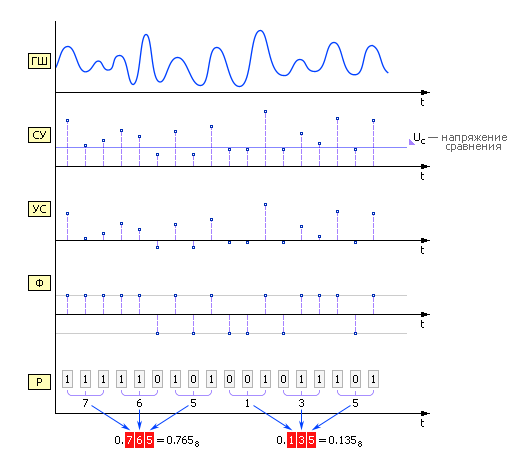
Рис. 9.5. Диаграмма получения случайных чисел аппаратным методом

Задача «Генерация случайных чисел при помощи монеты»

Сгенерируйте случайное трехразрядное число, распределенное по равномерному закону в интервале от 0 до 1, с помощью монеты. Точность — три знака после запятой.

Первый способ решения задачи
Подбросьте монету 9 раз, и если монета упала решкой, то запишите «0», если орлом, то «1». Итак, допустим, что в результате эксперимента получили случайную последовательность 100110100.

Начертите интервал от 0 до 1. Считывая числа в последовательности слева направо, разбивайте интервал пополам и выбирайте каждый раз одну из частей очередного интервала (если выпал 0, то левую, если выпала 1, то правую). Таким образом, можно добраться до любой точки интервала, сколь угодно точно.

Итак, 1: интервал [0; 1] делится пополам — [0; 0.5] и [0.5; 1], — выбирается правая половина, интервал сужается: [0.5; 1]. Следующее число, 0: интервал [0.5; 1] делится пополам — [0.5; 0.75] и [0.75; 1], — выбирается левая половина [0.5; 0.75], интервал сужается: [0.5; 0.75]. Следующее число, 0: интервал [0.5; 0.75] делится пополам — [0.5; 0.625] и [0.625; 0.75], — выбирается левая половина [0.5; 0.625], интервал сужается: [0.5; 0.625]. Следующее число, 1: интервал [0.5; 0.625] делится пополам — [0.5; 0.5625] и [0.5625; 0.625], — выбирается правая половина [0.5625; 0.6250], интервал сужается: [0.5625; 0.6250].

По условию точности задачи решение найдено: им является любое число из интервала [0.5625; 0.6250], например, 0.625.

В принципе, если подходить строго, то деление интервалов нужно продолжить до тех пор, пока левая и правая границы найденного интервала не СОВПАДУТ между собой с точностью до третьего знака после запятой. То есть с позиций точности сгенерированное число уже не будет отличимо от любого числа из интервала, в котором оно находится.

Второй способ решения задачи
Разобьем полученную двоичную последовательность 100110100 на триады: 100, 110, 100. После перевода этих двоичных чисел в десятичные получаем: 4, 6, 4. Подставив спереди «0.», получим: 0.464. Таким методом могут получаться только числа от 0.000 до 0.777 (так как максимум, что можно «выжать» из трех двоичных разрядов — это 111₂ = 7₈) — то есть, по сути, эти числа представлены в восьмеричной системе счисления. Для перевода восьмеричного числа в десятичное представление выполним:
0.464₈ = 4 · 8^–1 + 6 · 8^–2 + 4 · 8^–3 = 0.6015625₁₀ = 0.602₁₀.
Итак, искомое число равно: 0.602.

Табличные ГСЧ

Табличные ГСЧ в качестве источника случайных чисел используют специальным образом составленные таблицы, содержащие проверенные некоррелированные, то есть никак не зависящие друг от друга, цифры. В табл. 9.1 приведен небольшой фрагмент такой таблицы. Обходя таблицу слева направо сверху вниз, можно получать равномерно распределенные от 0 до 1 случайные числа с нужным числом знаков после запятой (в нашем примере мы используем для каждого числа по три знака). Так как цифры в таблице не зависят друг от друга, то таблицу можно обходить разными способами, например, сверху вниз, или справа налево, или, скажем, можно выбирать цифры, находящиеся на четных позициях.

Таблица 9.1. Случайные цифры. Равномерно распределенные от 0 до 1 случайные числа

Случайные цифры Равномерно распределенные от 0 до 1 случайные числа 0.929 0.204 0.269 … …

Достоинство данного метода в том, что он дает действительно случайные числа, так как таблица содержит проверенные некоррелированные цифры. Недостатки метода: для хранения большого количества цифр требуется много памяти; большие трудности порождения и проверки такого рода таблиц, повторы при использовании таблицы уже не гарантируют случайности числовой последовательности, а значит, и надежности результата.

Ниже находится таблица, содержащая 500 абсолютно случайных проверенных чисел (взято из книги И. Г. Венецкого, В. И. Венецкой «Основные математико-статистические понятия и формулы в экономическом анализе»).

5489 5583 3156 0835 1988 3912 0938 7460 0869 4420 3522 0935 7877 5665 7020 9555 7379 7124 7878 5544 7555 7579 2550 2487 9477 0864 2349 1012 8250 2633 5759 3554 5080 9074 7001 6249 3224 6368 9102 2672 6303 6895 3371 3196 7231 2918 7380 0438 7547 2644 7351 5634 5323 2623 7803 8374 2191 0464 0696 9529 7068 7803 8832 5119 6350 0120 5026 3684 5657 0304 3613 1428 1796 8447 0503 5654 3254 7336 9536 1944 5143 4534 2105 0368 7890 2473 4240 8652 9435 1422 9815 5144 7649 8638 6137 8070 5345 4865 2456 5708 5780 1277 6316 1013 2867 9938 3930 3203 5696 1769 1187 0951 5991 5245 5700 5564 7352 0891 6249 6568 4184 2179 4554 9083 2254 2435 2965 5154 1209 7069 2916 2972 9885 0275 0144 8034 8122 3213 7666 0230 5524 1341 9860 6565 6981 9842 0171 2284 2707 3008 0146 5291 2354 5694 0377 5336 6460 9585 3415 2358 4920 2825 5238 5402 7937 1993 4332 2327 6875 5230 7978 1947 6380 3425 7267 7285 1130 7722 0164 8573 7453 0653 3645 7497 5969 8682 4191 2976 0361 9334 1473 6938 4899 5348 1641 3652 0852 5296 4538 4456 8162 8797 8000 4707 1880 9660 8446 1883 9768 0881 5645 4219 0807 3301 4279 4168 4305 9937 3120 5547 2042 1192 1175 8851 6432 4635 5757 6656 1660 5389 5470 7702 6958 9080 5925 8519 0127 9233 2452 7341 4045 1730 6005 1704 0345 3275 4738 4862 2556 8333 5880 1257 6163 4439 7276 6353 6912 0731 9033 5294 9083 4260 5277 4998 4298 5204 3965 4028 8936 5148 1762 8713 1189 1090 8989 7273 3213 1935 9321 4820 2023 2589 1740 0424 8924 0005 1969 1636 7237 1227 7965 3855 4765 0703 1678 0841 7543 0308 9732 1289 7690 0480 8098 9629 4819 7219 7241 5128 3853 1921 9292 0426 9573 4903 5916 6576 8368 3270 6641 0033 0867 1656 7016 4220 2533 6345 8227 1904 5138 2537 0505 2127 8255 5276 2233 3956 4118 8199 6380 6340 6295 9795 1112 5761 2575 6837 3336 9322 7403 8345 6323 2615 3410 3365 1117 2417 3176 2434 5240 5455 8672 8536 2966 5773 5412 8114 0930 4697 6919 4569 1422 5507 7596 0670 3013 1351 3886 3268 9469 2584 2653 1472 5113 5735 1469 9545 9331 5303 9914 6394 0438 4376 3328 8649 8327 0110 4549 7955 5275 2890 2851 2157 0047 7085 1129 0460 6821 8323 2572 8962 7962 2753 3077 8718 7418 8004 1425 3706 8822 1494 3837 4098 0220 1217 4732 0150 1637 1097 1040 7372 8542 4126 9274 2251 0607 4301 8730 7690 6235 3477 0139 0765 8039 9484 2577 7859 1976 0623 1418 6685 6687 1943 4307 0579 8171 8224 8641 7034 3595 3875 6242 5582 5872 3197 4919 2792 5991 4058 9769 1918 6859 9606 0522 4993 0345 8958 1289 8825 6941 7685 6590 1932 6043 3623 1973 4112 1795 8465 2110 8045 3482 0478 0221 6738 7323 5643 4767 0106 2272 9862

Алгоритмические ГСЧ

Числа, генерируемые с помощью этих ГСЧ, всегда являются псевдослучайными (или квазислучайными), то есть каждое последующее сгенерированное число зависит от предыдущего:

r_{i + 1} = f(r_i).

Последовательности, составленные из таких чисел, образуют петли, то есть обязательно существует цикл, повторяющийся бесконечное число раз. Повторяющиеся циклы называются периодами.

Достоинством данных ГСЧ является быстродействие; генераторы практически не требуют ресурсов памяти, компактны. Недостатки: числа нельзя в полной мере назвать случайными, поскольку между ними имеется зависимость, а также наличие периодов в последовательности квазислучайных чисел.

Рассмотрим несколько алгоритмических методов получения ГСЧ: