| Угол в воздухе, град | Угол в воде, град |
| | 7,5 49,5 |
Впервые общий принцип, наглядно объясняющий закон поведения света, был предложен французским математиком Пьером де Ферма примерно в 1650 г. и получил название принципа наименьшего времени, или принципа Ферма. Идея его состоит в следующем: свет выбирает из всех возможных путей, соединяющих две точки, тот путь, который требует наименьшего времени для его прохождения.
Покажем вначале, что это верно для случая с зеркалом, что этот простой принцип объясняет и прямолинейность распространения света, и закон отражения света от зеркала.
| Рис. 9.3. Иллюстрация принципа наименьшего времени |
Попытаемся решить следующую задачу. На рис. 9.3 изображены две точки А и В и плоское зеркало ММ`. Каким путем можно за кратчайшее время попасть из точки А в точку В? Ответ: по прямой, проведенной из А в В. Но если мы добавим дополнительное условие, что свет должен попасть на зеркало, отразиться от него и вернуться снова в точку В опять таки за кратчайшее время, то ответить не так уж просто. Один путь – как можно скорее добраться до зеркала, а оттуда в точку В, т.е. по пути ADB. Путь DB, конечно, длинен. Если сдвинуться чуть-чуть вправо в точку Е, то первый отрезок пути немного увеличится, но зато сильно уменьшится второй, и время прохождения поэтому станет меньше. Как найти точку С, для которой время прохождения наименьшее? Воспользуемся для этого хитроумным геометрическим приемом.
По другую сторону зеркала MM`, на таком же расстоянии от него, что и точка В, строим искусственную точку B`. Затем проведем линию ЕВ`. Поскольку угол BFM прямой и BF = FB`, то ЕВ = ЕВ`. Следовательно, сумма длин двух отрезков АЕ+ЕВ, пропорциональная времени их прохождения (если свет идет с постоянной скоростью), равна сумме длин AE+EB`. Теперь нужно выяснить, когда сумма длин будет наименьшей. Ответ: когда точка С будет лежать на прямой, соединяющей А и В`! Другими словами, нужно идти к мнимой точке В` (мнимому изображению точки В) и тогда мы найдем точку С. Далее, если АСВ` - прямая линия, угол BCF равен углу B`CF и, следовательно, углу АСМ. Таким образом, утверждение о равенстве углов падения и отражения равносильно утверждению, что свет при отражении от зеркала в точку В выбирает путь, требующий наименьшего времени. Еще Герон Александрийский высказывал утверждение, что свет при отражении идет от одной точки в другую по кратчайшему пути. Так что идея принципа, как видим, не нова. Именно это вдохновило Ферма, и он попробовал применить этот принцип к явлению преломления. Но свет, преломляясь, очевидным образом идет не по кратчайшему пути, и тогда Ферма предложил другой принцип – свет выбирает путь, время прохождения по которому наименьшее.
Прежде чем перейти к вопросу о преломлении света, сделаем еще одно замечание об отражении от зеркала. Если поместить источник света в точку В и направить луч на зеркало, то свет, отражаясь от зеркала, пройдет из В в А так, как будто бы источник находится в В`, а зеркала нет вообще. Наш глаз видит только тот свет, который действительно входит в него. И хотя источник расположен в точке В, зеркало направляет свет в глаз точно так, как будто источник находится в В`, и система «глаза-мозг» интерпретирует именно так это явление. Поэтому иллюзия, что источник или предмет находится за зеркалом, вызывается только тем фактом, что свет попадает в глаз физически именно так, как если бы предмет действительно находился позади зеркала (если не принимать во внимание пыль на зеркале и то, что нам известно, что зеркало реально существует, и другие сведения, которые учитывает наш мозг).
Покажем теперь, что из принципа наименьшего времени вытекает закон Снелла для преломления. При этом мы должны, конечно, что-то предположить относительно скорости света в воде. Будем считать, что скорость света в воде меньше скорости света в воздухе, и отношение второй скорости к первой обозначим через n.
Наша задача, иллюстрируемая рис. 9.4, по-прежнему состоит в том, чтобы попасть из точки А в точку В за наименьшее время.
| Рис. 9.4. Иллюстрация принципа Ферма для случая преломления |
Чтобы убедиться, что путь по прямой здесь не самый быстрый, представим себе следующую ситуацию. Хорошенькая девушка падает из лодки в воду в точке В и кричит, что не умеет плавать и просит спасти ее. Линия Х – это берег. Вы находитесь на суше в точке А и видите, что произошло, вы умеете плавать и умеете бегать. Но бегаете вы быстрее, чем плаваете. Что вам делать? Бежать по прямой к берегу и плыть к девушке? Надо бы! Но, немного поразмыслив, вы поймете, что выгоднее пробежать несколько дольше по берегу, чтобы уменьшить ваш путь в воде, потому что в воде вы будете двигаться гораздо медленнее. Рассуждая таким образом, лучше всего было бы заранее тщательно вычислить путь! Попытаемся показать, что окончательное решение задачи – это путь АСВ, который занимает из всех возможных наименьшее время. Если этот путь кратчайший по времени, то любой другой окажется длиннее. Поэтому, если отложить на графике зависимость времени от положения точки Х, получится кривая, похожая на изображенную на рис. 9.5, где точка С соответствует наименьшему времени. Это означает, что для точек Х вблизи С в первом приближении время прохождения практически одинаковое, так как в точке С наклон кривой равен нулю.
| Рис. 9.5. Наименьшее время получается при выборе точки С. Соседние точки приводят примерно к такому же времени прохождения |
Итак, при небольшом изменении положения точки время прохождения не менялось. Конечно, возникнут бесконечно малые изменения времени второго порядка, и они должны быть положительными при смещении в обе стороны от точки С. Возьмем близкую точку Х, вычислим время прохождения на пути АХВ и сравним его со старым путем АСВ. Сделать это очень просто. Конечно, нужно еще, чтобы разность времен стремилась к нулю для малых расстояний ХС. Обратимся сначала к пути по суше. Если мы опустим перпендикуляр ЕХ, то легко увидим, что наш путь стал короче на длину ЕС. Можно сказать, что это расстояние мы выиграли. С другой стороны, опустив перпендикуляр CF, мы увидим, что в воде придется проплыть дополнительное расстояние XF. В этом мы проиграли. С точки зрения экономии времени выигрывается время на отрезке ЕС, но теряется на отрезке XF. Эти два интервала времени должны быть равны, так как в первом приближении полное время прохождения не меняется. Предположив, что скорость в воде равна скорости в воздухе, умноженной на 1/n, получим
EC = nXF (9.3)
Поэтому мы видим, что если нам удалось правильно выбрать точку С (ХС sin EXC = nXC sin XCF) или мы сократили путь на длину общей гипотенузы ХС и заметили, что
EXC = ECN = θi и XCF = BCN` = θr,
то мы получим
sin θi = n sin θr. (9.4)
Отсюда видно, что при отношении скоростей, равном n, свет должен двигаться из одной точки в другую по такому пути, чтобы отношение синусов θi и θr было равно отношению скоростей в двух средах.
Применения принципа Ферма
Рассмотрим теперь некоторые интересные следствия принципа наименьшего времени.
Первое из них – принцип обратимости. Мы уже нашли путь из А в В, требующий наименьшего времени, пойдем теперь в обратном направлении, считая, что скорость света не зависит от направления. Наименьшему времени отвечает та же траектория, и, следовательно, если свет распространяется по некоторому пути в одном направлении, то он будет двигаться по этому же пути и в обратном направлении.
Другой интересный пример. На пути света под некоторым углом поставлена четырехгранная стеклянная призма с параллельными гранями (рис. 9.6). Свет проходит из точки А в В и, встретив на своем пути призму, отклоняется, причем длительность пути в призме уменьшается за счет изменения наклона траектории, а путь в воздухе немного удлиняется. Участки траектории вне призмы оказываются параллельными друг другу, потому что углы входа и выхода из призмы одинаковы.
| Рис. 9.6. Луч света, выходящий из прозрачной пластины, параллелен падающему лучу |
Третье интересное явление состоит в том, что когда мы смотрим на заходящее солнце, то оно на самом деле находится уже ниже линии горизонта! Нам кажется, что солнце еще над горизонтом, а оно фактически уже зашло (рис. 9.7). Дело здесь в следующем. Земная атмосфера вверху разрежена, а в нижних слоях более плотная. Свет распространяется в воздухе медленнее, чем в вакууме, и поэтому солнечные лучи достигнут какой-то точки за горизонтом быстрее, если будут двигаться не по прямой линии, а по траектории с более крутым наклоном в плотных слоях атмосферы, сокращая, таким образом, свой путь в этих слоях.
| К кажущемуся положению Солнца |
| К истинному положению Солнца |
| Рис. 9.7. У горизонта Солнце кажется на ½ градуса выше, чем на самом деле |
Еще пример такого же рода – мираж, который часто наблюдают путешественники на раскаленных солнцем дорогах. Они видят на дороге «воду», а когда подъезжают туда, то кругом оказывается все сухо, как в пустыне! Сущность явления в следующем. То, что мы видим в этом случае, это «отраженный» дорогой свет. На рис. 9.8 показано, как падающий на дорогу луч света попадает к нам в глаз. Почему? Воздух сильно раскален над самой дорогой, а в верхних слоях холоднее. Горячий воздух, расширяясь, становится более разреженным, а потому и скорость света в нем больше, чем в более прохладном. Другими словами, свет быстрее проходит в теплых слоях, чем в прохладных. Поэтому свет проходит не по прямой, а идет по траектории с наименьшим временем, заворачивая для этого в теплые слои воздуха, чтобы сократить время. Таким образом, свет идет по кривой.
| Раскаленный асфальт или песок дороги |
Легко показать, что принцип Ферма предсказывает ряд новых фактов. Прежде всего, принцип наименьшего действия совпадает с законом равенства углов при отражении и пропорциональности синусов углов при преломлении. Предположим, что имеются три среды – стекло, вода и воздух и мы наблюдаем явление преломления и измеряем показатель n для перехода из одной среды в другую. Обозначим через n12 показатель преломления для перехода из воздуха (1) в воду (2), а через n13 – для перехода из воздуха (1) в стекло (3). Измерив преломление в системе вода-стекло, найдем еще один показатель преломления и обозначим его n23. Здесь заранее нет оснований считать, что n12, n13 и n23 связаны между собой. Если же исходить из принципа наименьшего времени, то такую связь можно установить. Показатель n12 есть отношение двух величин – скорости света в воздухе к скорости света в воде; показатель n13 есть отношение скорости света в воздухе к скорости света в стекле, а n23 есть отношение скорости света в воде к скорости света в стекле. Поэтому, сокращая скорость света в воздухе, получаем
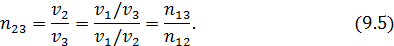
Другими словами, мы предсказываем, что показатель преломления для перехода из одного материала в другой можно получить из показателей преломления каждого материала по отношению к некоторой среде, скажем воздуху или вакууму. Таким образом, измерив скорость света во всех средах, мы образуем одно число для каждой среды – показатель преломления для перехода из вакуума в среду – и называем его ni (например, ni для воздуха есть отношение скорости в воздухе к скорости в вакууме и т.д.), после чего легко написать нужную формулу. Показатель преломления для любых двух материалов i и j равен

Используя только закон Снелла, подобное соотношение предсказать невозможно. Но связь эта существует. Соотношение (9.6) известно давно и послужило сильным аргументом в пользу принципа наименьшего времени.