Тела вращения и их изображения

План лекции:

1. Шар и его изображение. Цилиндр и его изображение.

2. Конус и его изображение.

1. Шар - одна из простейших фигур, обладающая разнооб­разными свойствами. Некоторые из них были известны еще древнегреческим математикам.

Поверхность шара называется сферой. Определяются сфера и шар аналогично тому, как определяются окружность и круг на плоскости.

Сферой называется множество точек пространства, уда­ленных от данной точки на заданное положительное расстоя­ние. При этом данная точка называется центром сферы, а данное расстояние - ее радиусом.

Шаром называется множество точек пространства, нахо­дящихся от данной точки на расстоянии, не большем некото­рого данного положительно расстояния. Данная точка - это центр шара, а данное расстояние - радиус шара.

Заметим, что радиусом шара и сферы называют не только расстояние, но также любой отрезок, соединяющий их центр с точкой на сфере.

Диаметр шара и сферы - это любой отрезок, соединяющий две точки сферы и проходящий через центр, а также длина этого отрезка.

Если шар пересечь плоскостью, проходящей через его центр, то пересечением будет круг, радиус которого совпадает с радиусом шара. Этот круг называют большим кругом, а его окружность - большой окружностью или экватором.

При параллельном проектировании шар изображается в виде круга того же радиуса. Чтобы сделать изображение шара более наглядным, рисуют проекцию какой-нибудь большой окружности, плоскость которой не перпендикулярна плоскости проекции. Эта проекция будет эллипсом. Центр шара изобразится центром этого эллипса

Теперь можно найти соответствующие полюсы N и S при условии, что отрезок, их соединяющий, перпендикулярен плоскости экватора. Для этого через точку О проводим прямую, перпендикулярную АВ и отмечаем точку С – пересечение этой прямой с эллипсом; затем через точку С проводим касательную к эллипсу, изображающему экватор. Доказано, что расстояние СМ равно расстоянию от центра шара до каждого из полюсов. Поэтому, отложив отрезки ON и OS, равные СМ, получим полюсы N и S.

Рассмотрим один из приемов построения эллипса: строят окружность с диаметром и проводят хорды, перпендикуляр­ные диаметру (рис. 171). Половину каждой из хорд делят по­полам и полученные точки соединяют плавной кривой. Эта кривая - эллипс, большой осью которого является, а центром - точка О.

2. Прямой круговой цилиндр - геомет­рическое тело, образованное заключенны­ми между двумя параллельными плоско­стями отрезками всех параллельных пря­мых, пересекающих круг в одной из плос­костей, и перпендикулярных плоскостям оснований (рис. 172).

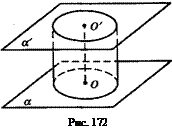Радиусом цилиндра называется радиус окружности его ос­нования. Высотой цилиндра называется расстояние между плоскостями его оснований. Его осью называется прямая, проходящая через центры ок­ружностей оснований

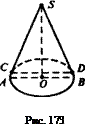
3. . Конусом называется тело, об­разованное всеми отрезками, соединяющими данную точку - его вершину - с точками некото­рого круга - основания конуса.

Отрезки, соединяющие вер­шину конуса с точками окружности основания, называются его образующими. центр основания - точку О и перпендикулярно проводят отрезок OS, который изображает высоту конуса. Из точки S проводят к эллипсу касательные (это делают на глаз, прикладывая линейку) и выделяют отрезки SC и SD этих прямых от точки S до точек касания С и D. Заме­тим, что отрезок CD не совпадает с диа­метром основания конуса (рис. 173).

Конус называется прямым, если прямая, соединяющая его вершину с центром окружности основания, перпендикулярна основанию.

Высотой конуса называется расстояние от его вершины до основания.

Литература

1. Стойлова, Л.П. Математика [Текст]: учеб.пособие для студентов средн. пед. учеб. заведений – 3 –е изд., испр. – М.: Издательский центр «Академия», 1998.

2. Стойлова, Л.П., Пышкало, А.М. Основы начального курса математики [Текст]: Учебное пособие для учащихся педучилищ по специальности №2001 «Преподавание в начальных классах общеобразовательных школ». – М.: Просвещение, 1988.

3. Виленкин, Н.Я., Пышкало, А.М., Стойлова, Л.П. Математика [Текст]: учеб. пособие для студентов пединститутов по специальности №2121 «Педагогика и методика начального обучения». – М.: Просвещение. 1977.

4. Погорелов А.В. Геометрия: Учеб. для 7 - 11 кл. общеобразоват. учреждений. - М.: Просвещение, 1997.

РАЗДЕЛ 3 .НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ

ТЕМА Аксиоматическое построение системы натуральных чисел

Как уже было сказано, натуральные числа получаются при счете предметов и при измерении величин. Но если при изме­рении появляются числа, отличные от натуральных, то счет приводит только к числам натуральным. Чтобы вести счет, нужна последовательность числительных, которая начинается с единицы и которая позволяет осуществлять переход от од­ного числительного к другому и столько раз, сколько это необходимо. Иначе говоря, нужен отрезок натурального ряда. Поэтому, решая задачу обоснования системы натуральных чисел, в первую очередь надо было ответить на вопрос о том, что же представляет собой число как элемент натурального ряда. Ответ на него был дан в работах двух математиков - немца Грассмана и итальянца Пеано. Они предложили аксио­матику, в которой натуральное число обосновывалось как элемент неограниченно продолжающейся последовательности.

Основные понятия и аксиомы. Определение натурального числа

В качестве основного понятия при аксиоматическом по­строении арифметики натуральных чисел взято отношение «непосредственно следовать за », заданное на непустом мно­жестве N.

Элемент, непосредственно следующий за элементом а, обо­значают а'.

Суть отношения «непосредственно следовать за » раскры­вается в следующих аксиомах.

Аксиома 1. В множестве N существует элемент, непосред­ственно не следующий ни за каким элементом этого множест­ва. Будем называть его единицей и обозначать символом 1.

Аксиома 2. Для каждого элемента а из N существует единственный элемент а', непосредственно следующий за а.

Аксиома 3. Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а.

Аксиома 4. Всякое подмножество М множества N, обла­дающее свойствами: 1) 1 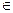М; 2) из того, что а содержится в М, следует, что и а' содержится в М, совпадает с множеством N.

Сформулированные аксиомы часто называют аксиомами Пеано.

Используя отношение «непосредственно следовать за» и аксиомы 1-4, можно дать следующее определение натураль­ного числа.

Определение. Множество N, для элементов которого установлено отношение «непосредственно следовать за », удовлетворяющее аксиомам 1-4, называется множест­вом натуральных чисел, а его элементы - натуральными числами.

Выбирая в качестве множества N некоторое конкретное мно­жество, на котором задано конкретное отношение «непосред­ственно следовать за », удовлетворяющее аксиомам 1-4, мы получим модель данной системы аксиом.

Стандартной моделью системы аксиом Пеано является возникший в процессе исторического развития обще­ства ряд чисел:

1,2,3,4,...

Каждое число этого ряда имеет свое обозначение и назва­ние, которое мы будем считать известными.

Определение. Если натуральное число b непосредственно следует за натуральным числом а, то число а называется непосредственно предшествующим (или предшествую­щим) числу b.

Отношение «предшествует» обладает рядом свойств. Они формулируются в виде теорем и доказываются с помощью аксиом 1-4.

Теорема 1. Единица не имеет предшествующего нату­рального числа.

Истинность данного утверждения вытекает сразу из ак­сиомы 1.

Теорема 2. Каждое натуральное число а, отличное от 1, имеет предшествующее число b, такое, что

b' = а.

Аксиоматическое построение теории натуральных чисел не рассматривается ни в начальной, ни в средней школе. Однако те свойства отношения «непосредственно следовать за », кото­рые нашли отражение в аксиомах Пеано, являются предметом изучения в начальном курсе математики. Уже в первом классе при рассмотрении чисел первого десятка выясняется, как мо­жет быть получено каждое число. При этом используются понятия «следует» и «предшествует». Каждое новое число выступает как продолжение изученного отрезка натурального ряда чисел. Учащиеся убеждаются в том, что "за каждым чис­лом идет следующее, и притом только одно, что натуральный ряд чисел бесконечен. И, конечно, знание аксиоматической теории поможет учителю методически грамотно организовать усвоение детьми особенностей натурального ряда чисел.