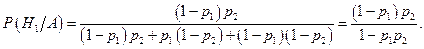Формула Байеса (формула гипотез)

Пусть имеется полная группа несовместных гипотез 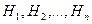с известными вероятностями их наступления 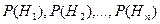. Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности .

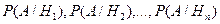Требуется определить какие вероятности имеют гипотезы 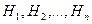относительно события А, т.е. условные вероятности .

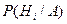Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события:

.

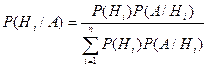Эта формула называется формулой Байеса.

Доказательство.По теореме умножения вероятностей находим:

.

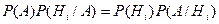Тогда если 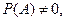то 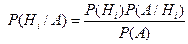. Для нахождения вероятности 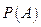используем формулу полной вероятности:

.

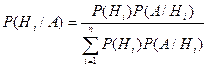Если до испытания все гипотезы равновероятны с вероятностью 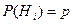, то формула Байеса принимает вид:

.

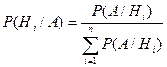Пример. Трое охотников одновременно выстрелили по медведю, который был убит одной пулей. Определить вероятность того, что медведь был убит первым стрелком, если вероятности попадания для этих стрелков равны соответственно 0,3, 0,4, 0,5.

В этой задаче требуется определить вероятность гипотезы уже после того, как событие уже совершилось. Для определения искомой вероятности надо воспользоваться формулой Байеса. В нашем случае она имеет вид:

,

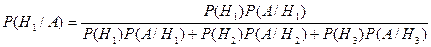где 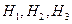– гипотезы, что медведя убьет первый, второй и третий стрелок соответственно. До произведения выстрелов эти гипотезы равновероятны и их вероятность равна 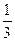. Вероятность того, что медведя убил первый стрелок при условии, что выстрелы уже произведены (событие А) имеет вид .

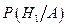Вероятности того, что медведя убьет первый, второй или третий стрелок, вычисленные до выстрелов, равны соответственно:

;

;

,

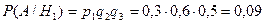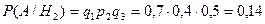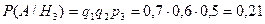где 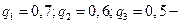вероятности промаха для каждого из стрелков, рассчитаны по формуле 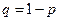, где р – вероятности попадания для каждого из стрелков.

Подставим эти значения в формулу Байеса, находим:

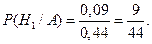
Пример. Известно, что 96 % выпускаемой продукции удовлетворяет стандарту. Отдел технического контроля признаёт пригодной стандартную продукцию с вероятностью 0,98 и нестандартную - с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее контроль, удовлетворяет стандарту.

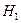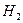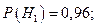
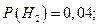
Обозначим через А-событие, что изделие прошло контроль. Гипотезы: - изделие удовлетворяет стандарту, - изделие не удовлетворяет стандарту. Имеем 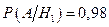(так называемый риск изготовителя, т.е. в 2% случаев годная продукция признается браком); 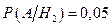(так называемый риск потребителя, т.е. в 5% случаев негодная продукция поступает к потребителю).

По условию задачи изделие прошло контроль, т.е. событие А произошло, и при этом условии необходимо определить вероятность стандартности изделия, т.е. гипотезы 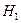. Следовательно, необходимо применить формулу Байеса:

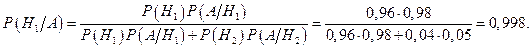
Пример. Прибор состоит из двух узлов: работа каждого узла безусловно необходима для работы прибора в целом. Надежность (вероятность безотказной работы в течении времени t (первого узла равна 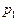, второго- 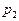. Прибор испытывали в течении времени t, в результате чего обнаружено, что он вышел из строя ( отказал ). Найти вероятность того, что отказал только первый узел, а второй исправен.

До опыта возможны четыре гипотезы:

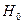- оба узла исправны;

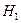- первый узел отказал, а второй исправен;

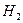- первый узел исправен, а второй отказал;

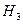- оба узла отказали.

Прибор работоспособен только при выполнении гипотезы 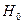, а при других гипотезах он отказывает, т.е.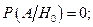 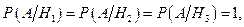где А- отказ прибора.

Так как известно, что событие А произошло, необходимо найти сначала условную вероятность 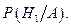Определим сначала вероятности гипотез:

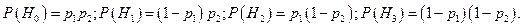
По формуле Байеса находим: