Раскрытие неопределенностей

При определении пределов часто возникают ситуации, называемые неопределенностями. Мы рассмотрим неопределенности следующих видов

1) 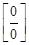– неопределенность “ноль делить на ноль”.

2) – неопределенность “бесконечность делить на бесконечность”.

3) 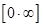–неопределенность “ноль умножить на бесконечность”.

Нахождение пределов в этих случаях называется раскрытием неопределенностей.

Рассмотрим некоторые приемы раскрытия каждой неопределенности в отдельности.

Неопределенность 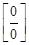появляется при нахождении предела отношения двух бесконечно малых функций .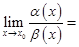

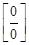Пример 1.4

.

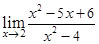Здесь 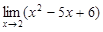= 4 – 10 + 6 = 0 и 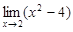= 0. Числитель и знаменатель дроби являются бесконечно малыми при 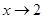, т.е. имеет место неопределенность 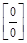. Для раскрытия неопределенности в рассматриваемом случае числитель и знаменатель дроби разложим на множители и сократим на величину 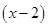, дающую 0 в числителе и знаменателе:

= = = = = – .

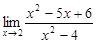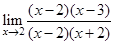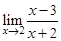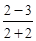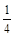Пример 1.5

Найти предел: .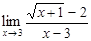

Решение

Здесь также имеем дело с неопределенностью 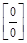. Для раскрытия этой неопределенности умножим числитель и знаменатель дроби на выражение 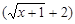, которое называется сопряженным выражению 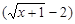, тогда

= = = =

= = = .

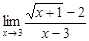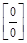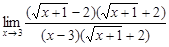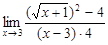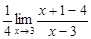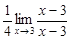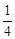Для раскрытия неопределенности 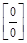в некоторых случаях могут быть полезны следующие определения и теоремы.

Определение 1.1. Пусть 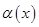и 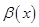две БМ при 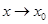. Если

,

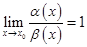(1.1)

то БМ 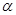и 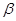называются эквивалентными. Эквивалентность БМ 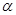и 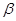обозначается .

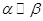Теорема 1.1. (Первый замечательный предел). Можно показать

[ ], что

,

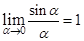(1.2)

Предел (1.2) называется первым замечательным пределом. Из теоремы 1.1 и определения 1.1 следует, что 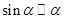. Приведем еще некоторые примеры эквивалентных БМ при a® 0:

Таблица 1.1

1.	sina ~	a
2.		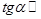a
3.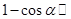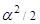
4.		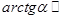a
5.		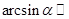a
6.		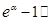a

Теорема 1.2.

Предел отношения двух бесконечно малых величин равен пределу отношения бесконечно малых, эквивалентных данным.

Поясним, что утверждает теорема. Пусть 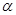и 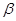две бесконечно малые функции. Известны еще две БМ 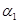и 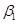, причем 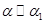и 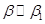. Тогда .

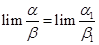Доказательство:

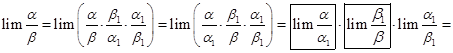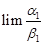= , что и требовалось. доказать.

Каждый из пределов в рамках равен единице, т.к. это пределы отношений эквивалентных бесконечно малых.

Пример 1.6

Найти .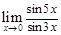

Решение

Здесь имеет место неопределенность 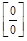, которая раскрывается

переходом к эквивалентным величинам: sin5x~5x, sin3x~3x, по теореме 1.2 получаем:

= = = .

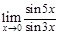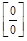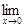
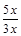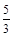Неопределенность появляется при нахождении предела отношения двух бесконечно больших .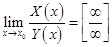

Пример 1.7

Найти .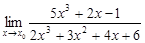

Решение

Здесь имеет место неопределенность . Отметим, что 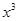самая большая степень, в которой переменная 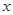входит в числитель и знаменатель дроби. Для раскрытия неопределенности вынесем 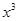за скобки и в числителе и в знаменателе и сократим. Получим

= =

= .

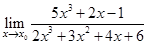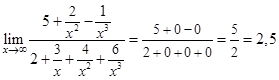Отметим, что в данном примере высшая степень 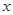в числителе равна высшей степени 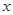в знаменателе. Предел равен отношению коэффициентов при высших степенях 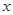в числителе и знаменателе.

Пример 1.8

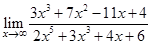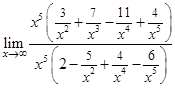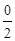= = = = 0.

Отметим, что в данном примере высшая степень 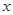в числителе меньше высшей степени 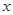в знаменателе. Предел равен нулю.

Пример 1.9

= = =

= = .

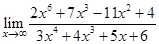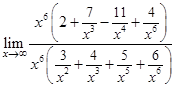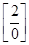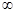В данном примере высшая степень 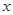в числителе больше высшей степени 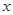в знаменателе. Предел равен бесконечности. В результате рассмотрения примеров 1.7, 1.8 и 1.9 сформулируем общее правило нахождения предела вида

=

=

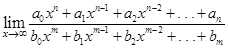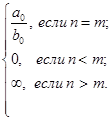
Пример 1.10

.

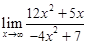Решение

Здесь 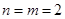, , 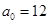, 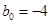поэтому предел равен :

.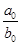
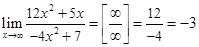