Основные уравнения динамики жидкости

Дифференциальные уравнения движения идеальной жидкости. Урав­нение Бернулли для установившегося движения идеальной жидкости. Гео­метрический и энергетический смысл уравнения Бернулли. Уравнение Бернулли для потока реальной жидкости. Коэффициент Кориолиса. Общие понятия о потерях. Виды гидравлических потерь.

Методические указания

Важным уравнением в гидравлике, применяемым на практике, явля­ется уравнение Бернулли:

,

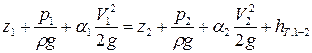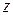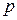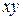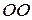где – геометрический напор; возвышение рассматриваемой точки (точки с давлением ) данного живого сечения над произвольно выбранной гори­зонтальной плоскостью сравнения или ; мера воздействия на поток силы тяжести; удельная потенциальная энергия положения относительно Земли, т.е. потенциальная энергия поля земного притяжения; 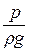– пьезометрический напор; возвышение уровня в пьезометрической трубке над точкой, имеющей ординату 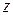; мера («пьезометрический» значит «давление меряющий») воздействия на поток силы давления: удельная потенциальная энергия давления; 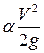– скоростной напор; возвышение уровня в трубке Пито, нижний открытый конец которой загнут против течения, над уров­нем в пьезометре; мера воздействия на поток конвективной силы инерции; удельная кинетическая энергия; высота взлета струи, выпущенной верти­кально вверх со скоростью 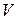; 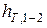– потерянный напор; понижение линии энергии (механической) на участке между сечениями 1 и 2, для которых составляется уравнение Бернулли; мера воздействия сил трения; удельная механическая энергия, перешедшая в тепловую на участке 1 – 2вследствие работы сил трения.

Уравнение Бернулли надо не только хорошо знать, понимать, но и уметь им пользоваться для решения практических задач, уметь составлять его для различных конкретных случаев, что достигается только практикой. Работая с уравнением Бернулли, полезно руководствоваться следующими указаниями:

1) уравнение Бернулли составляется для двух живых, т. е. нормальных к направлению скорости, сечений; эти сечения должны располагаться на прямолинейных участках потока;

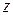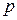2) одно из этих сечений следует брать там, где требуется определить или , или , или 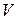; другое сечение рекомендуется брать там, где 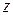, 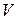и 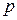известны;

3) нумеровать расчетные сечения следует так, чтобы жидкость двига­лась от 1-го ко 2-му; в противном случае должен быть изменен на обрат­ный знак ;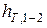

4) горизонтальную плоскость сравнения желательно по высоте совме­щать с тем из двух расчетных сечений, которое располагается ниже; тогда один из 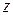выпадет из уравнения, а второй будет величиной положительной;

5) последний член уравнения должен учитывать все потери напора между расчетными сечениями.

Контрольные вопросы

1. Напишите дифференциальные уравнения движения идеальной жид­кости (уравнения Эйлера) и объясните физический смысл входящих в них членов.

2. Как записывается уравнение Бернулли для элементарной струйки идеальной жидкости? Каков геометрический и энергетический смысл каждого слагаемого в уравнении Бернулли?

3. Запишите уравнение Бернулли для элементарной струйки реальной (вязкой) жидкости. Каков геометрический и энергетический смысл каждого слагаемого в уравнении Бернулли?

4. Как записывается уравнение Бернулли для потока реальной жидко­сти? Пояснить геометрический и энергетический смысл его членов.

5. В чем состоит отличие уравнения Бернулли для элементарной струйки реальной жидкости от уравнения Бернулли потока реальной жидкости?

6. Каков физический смысл коэффициента Кориолиса (а) в уравнении Бернулли для потока реальной жидкости?

7. Укажите условие применения уравнения Бернулли для потока.

8. С какой целью вводится понятие о плавной изменяемости потока при выводе уравнения Бернулли для потока реальной жидкости?

9. Запишите уравнение Бернулли для двух сечений равномерного потока (например, в трубе) реальной жидкости, ось которого горизонтальна. Как изменяется давление по длине потока?

10. Может ли изменяться знак пьезометрического уклона от положи­тельного до отрицательного? В каких случаях? Может ли быть отрица­тельным гидравлический уклон?