Работа и мощность при вращательном движении
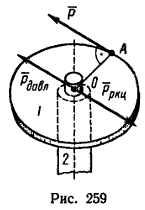
При вращательном движении тела движущим фактором является пара сил. Рассмотрим диск 1, могущий свободно вращаться вокруг оси 2 (рис. 259). Если к точке A на ободе диска приложить силу P (направим ее вдоль касательной к боковой поверхности диска; направленная таким образом сила называется окружным усилием), то диск станет вращаться. Вращение диска обусловлено появлением пары сил. Сила P, действуя на диск, прижимает его в точке O к оси (сила Pдавл на рис. 259, приложенная к оси 2) и возникает реакция оси (сила Pркц на рис. 259), приложенная так же, как и сила P, к диску. Так как все эти силы численно равны между собой и линии их действия параллельны, то силы P и Pркц образуют пару сил, которая и приводит диск во вращение.
Как известно, вращающее действие пары сил измеряется ее моментом, но момент пары сил равен произведению модуля любой из сил на плечо пары, поэтому вращающий момент
Mвр = Mпары = MOP = P*OA.
Единицей момента пары сил, а также момента силы относительно точки или относительно оси является 1 Н*м (ньютон-метр) в СИ и 1 кГ*м (килограмм-сила-метр) в системе МКГСС. Но при этом не следует смешивать эти единицы с единицами работы (1 Н*м=1 Дж или 1 кГ*м), имеющими ту же размерность.
Работу при вращательном движении производят пары сил.
Величина работы пары сил измеряется произведением момента пары (вращающего момента) на угол поворота, выраженный в радианах:
(1)A = Mврφ.
Таким образом, чтобы получить единицу работы, например, 1 Дж=1 Н*м, необходимо единицу момента 1 Н*м умножить на 1 рад. Но так как радиан – безразмерная величина
[радиан] = [длина дуги/радиус] = [м/м] = [1],
то
[Дж] = [Н*м] * [1] = [Н*м].
Мощность при вращательном движении
(2)N = A/t = Mврφ/t.
Если тело вращается с постоянной угловой скоростью, то, заменив в формуле (2) φ/t = ω, получим
(2')N = Mврω.
Если мощность того или иного двигателя – величина постоянная, то
(3)Mвр = N/ω,
т. е. вращающий момент двигателя обратно пропорционален угловой скорости его вала.
Это означает, что использование мощности двигателя при различных угловых скоростях позволяет изменять создаваемый им вращающий момент. Используя мощность двигателя при малой угловой скорости, можно получить большой вращающий момент.
Так как угловая скорость вращающейся части двигателя (ротора электродвигателя, коленчатого вала двигателя внутреннего сгорания и т. п.) при его работе практически не изменяется, то между двигателем и рабочей машиной устанавливается какой-либо механизм (редуктор, коробка скоростей и т. п.), могущий передавать мощность двигателя при различных угловых скоростях.
Поэтому формула (3), выражающая зависимость вращающего момента от передаваемой мощности и угловой скорости, имеет очень важное значение.
Используя при решении задач эту зависимость, необходимо иметь в виду следующее. Формула (3) применяется для решения задач, если мощность N задана в ваттах, а угловая скорость ω – в рад/сек (размерность [1/сек]), тогда вращающий момент Mврполучится в Н*м.
Задача 231. Для определения мощности электродвигателя через его шкив перекинута тормозная лента (рис. 260, а). Один конец ленты удерживается динамометром,...
Задача 232. Токарный станок приводится в движение электродвигателем, мощность которого N=2,21 кВт. Считая, что к резцу станка подводится лишь 0,8 мощности...
