Сравнение различных методов создания сетки
1) Определить среднее расстояние между точками данных, полученных при оцифровке карты «Горизонтали».
2) Создать по этим данным сеточные файлы с помощью всех доступных методов интерполяции, кроме последних трёх (Moving Average, Data Metrics, Local Polynomial). У метода «Полиномиальная регрессия» использовать по очереди 3 метода определения поверхности (Simple planar surface, Quadratic surface, Cubic surface). Каждый раз сохранять сетку в отдельном сеточном файле с именем, соответствующим названию метода интерполяции (например, «Горизонтали (IDP).grd», «Горизонтали (Kriging).grd», «Горизонтали (MinCurv).grd» и т. д.).
3) Обратить внимание на то, чтобы при построении сеточного файла пределы сетки не выходили за границы реальных значений. Например, при оцифровке растровой карты очень часто минимальные значения по X и Y могут быть меньше 0. Для исправления ситуации ввести по 0. Проверить также и максимум.
4) Создать новый плот-документ.
5) Построить в одном окне контурные карты на основе всех сеточных файлов. Расположить карты в виде мозаики и снабдить их подписями названий методов интерполяции.
6) Провести анализ полученных карт и попарное сопоставление каждой карты с картой, построенной с помощью метода Криге (пусть, например, он называется «Горизонтали (Криге).grd»). Указать сходства и отличия.
7) Сделать выводы об особенностях работы каждого метода интерполяции.
Построение сети – это создание регулярного массива значений Z-координат узловых точек по нерегулярному массиву (X, Y, Z)-координат исходных точек. Термин «нерегулярный массив координат» означает, что X, Y- координаты точек данных распределены по области карты неравномерно. Для создания карты изолиний (Contour) или графика поверхности (Surface) требуется регулярный массив узловых точек. Процедура построения сети представляет собой интерполяцию или экстраполяцию значений исходных точек данных на равномерно распределенные узлы в исследуемой области.
Программа Surfer предоставляет пользователю несколько методов по- строения регулярных сетей. Каждый из этих методов использует свою процедуру интерполяции данных, поэтому сети, построенные по вашим данным с помощью различных методов, могут несколько отличаться друг от друга.
Метод Криге (Kriging) – это геостатистический метод построения се- ти, который оказался очень полезным и в других областях. Данный метод пытается выразить тренды, которые предполагаются в ваших данных. Например, точки высокого уровня предпочтительнее соединять вдоль гребня, а не изолировать с помощью замкнутых горизонталей типа «бычий глаз».
Метод радиальных базисных функций (Radial Basis Functions) мно- гими авторами рассматривается как наилучший метод с точки зрения построения гладкой поверхности, проходящей через экспериментальные точки.
Триангуляция с линейной интерполяцией (Triangulation with Linear Interpolation) является точным интерполяционным методом. Суть этого метода заключается в следующем. Исходные точки данных соединяются таким образом, что результирующая поверхность покрывается «лоскутным одеялом» из граней треугольников. При этом ни одна из сторон треугольника не пересекается сторонами других треугольников. Каждый треугольник определяется тремя исходными экспериментальными точками. Значения функции в узлах регулярной сети, попадающих внутрь этого треугольника, принадлежат плоскости, проходящей через вершины треугольника.
Метод построения сеточной функции Inverse Distance to a Power (Степень обратного расстояния) основан на вычислении весовых коэффициентов, с помощью которых взвешиваются значения экспериментальных Z- 46 значений в точках наблюдений при построении интерполяционной функции. Вес, присвоенный отдельной точке данных при вычислении узла сети, пропорционален заданной степени (power) обратного расстояния от точки наблюдения до узла сети. При вычислении интерполяционной функции в каком-то узле сети сумма всех назначенных весов равна единице, а весовой коэффициент каждой экспериментальной точки является долей этого общего единичного веса. Если точка наблюдения совпадает с узлом сети, то весовой коэффициент этой точки полагается равным единице, а всем другим наблюденным точкам присваиваются нулевые веса. Другими словами, в этом случае узлу сети присваивается значение соответствующего наблюдения, и, следовательно, данный метод работает как точный интерполятор.
Метод Minimum Curvature (Минимальной кривизны) широко используется в науках о земле. Поверхность, построенная с помощью этого метода, аналогична тонкой упругой пленке, проходящей через все экспериментальные точки данных с минимальным числом изгибов. Метод минимальной кривизны, однако, не является точным методом. Он генерирует наиболее гладкую поверхность, которая проходит настолько близко к экспериментальным точкам, насколько это возможно, но эти экспериментальные точки не обязательно принадлежат интерполяционной поверхности.
Метод Polynomial Regression (Полиномиальной регрессии) используется для выделения больших трендов и структур в ваших данных. Это метод, строго говоря, не является интерполяционным методом, поскольку сгенерированная поверхность не проходит через экспериментальные точки.
Модифицированный метод Шепарда (Modified Shepard's Method) подобен методу обратных расстояний (Inverse Distance to a Power). Он также использует обратные расстояния при вычислении весовых коэффициентов, с помощью которых взвешиваются значения экспериментальных Z-значений в точках наблюдений. Отличие состоит в том, что при построении интерполяционной функции в локальных областях используется метод наименьших квадратов. Это уменьшает вероятность появления на сгенерированной поверхности структур типа «бычий глаз».
Как правило, при создании сеточного файла можно принять значения параметров сети по умолчанию; это позволяет сгенерировать приемлемый сеточный файл, пригодный для построения карт изолиний и графиков поверхностей. Однако есть несколько параметров, изменение которых оказывает существенное влияние на сеточный файл. Эти параметры по смыслу можно разбить на две группы: параметры геометрии сети и параметры используемого сеточного метода. Параметры геометрии сети (Grid Line Geometry) – это пределы сети (Grid Limits) и плотность сети (Grid Density).
Пределы сети определяют минимальные и максимальные значения X и Y координат создаваемого сеточного файла. По умолчанию Surfer выбирает в качестве пределов сети минимальные и максимальные значения X и Y координат точек данных из XYZ файла. Пределы сеточного файла задают область определения для карт изолиний и графиков поверхностей, которые будут строиться на основе этого файла. Плотность сети определяется количеством сеточных линий в на- правлении осей X и Y соответственно. Иными словами, плотности сети определяется числом строк и столбцов в сеточном файле. По умолчанию Surfer выбирает ту из осей координат (X или Y), которая длиннее, и строит 100 сеточных линий от этой оси. Сеточные линии от более короткой оси строятся с тем же шагом; их количество определяется длиной этой оси. Плотность сети определяется количеством строк и столбцов в сеточном файле, то есть числом узлов сети. С ростом плотности сети увеличивается гладкость изолиний и графиков поверхностей. Однако увеличение числа сеточных узлов пропорционально увеличивает время построения сети, размер сеточного файла, а также время рисования карт и графиков. Плотность сети определяет степень гладкости карт изолиний и графиков поверхностей. Изолинии, а также линии сетки, определяющей график поверхности, на самом деле являются ломаными линиями, состоящими из прямолинейных отрезков. Чем больше строк и столбцов в сеточном файле, тем короче эти отрезки и тем более гладкими выглядят изолинии и графики поверхностей. Выбор плотности сети следует производить в соответствии с исходными данными или требуемым масштабом карты. Если известен масштаб, в котором надо изобразить карту, то шаг между линиями сетки надо задать равным тому количеству единиц карты, которые помещаются в 1 мм изображения. Например, при масштабе 1:50 000 это будет 50 м. Если требуемый масштаб заранее не известен, то шаг между линиями сетки можно задать равным половине среднего расстояния между точками данных. В любом случае следует учитывать возможности компьютера, так как создание очень плотной сетки может затянуться надолго.
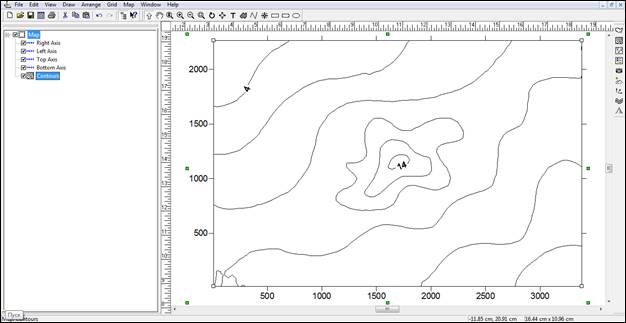
Рис. 28. Контурная карта созданная с помощью метода интерполяции Kriging
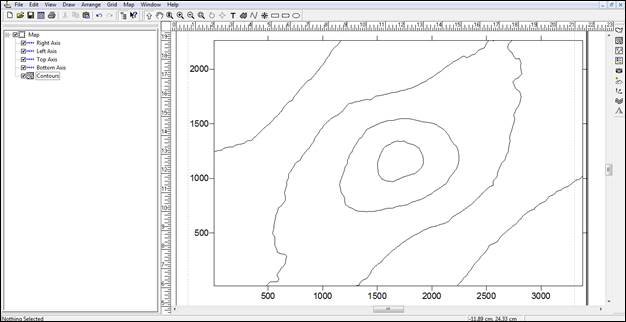
Рис. 29. Контурная карта созданная с помощью метода интерполяции Inverse Distance to a Power
- метод Inverse Distance to a Power даёт более сглаженные линии, особенно это видно в центре карты.
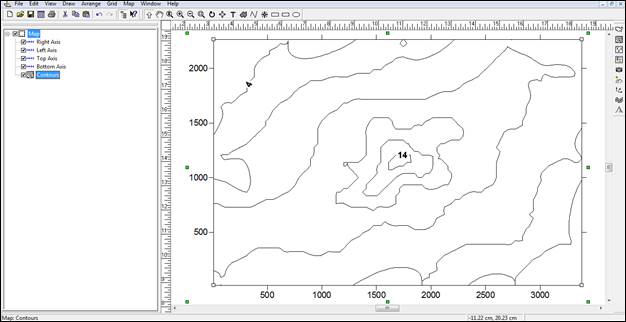
Рис. 30. Контурная карта созданная с помощью метода интерполяции Minimum Curvature
- метод Minimum Curvature даёт, наоборот, менее гладкие линии.
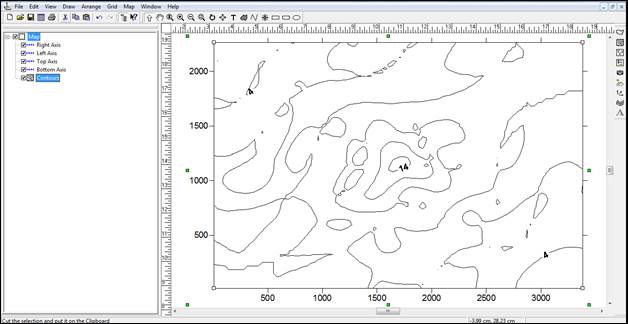
Рис. 31. Контурная карта созданная с помощью метода интерполяции Modified Shepard's Method
- метод Modified Shepard's Method даёт множество более мелких структур с сохранением общей картинки
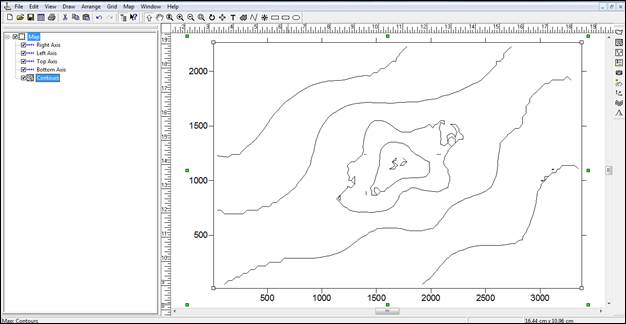
Рис. 32. Контурная карта созданная с помощью метода интерполяции Natural Neighbor
- Natural Neighbor сглаживает линии близкие к минимальному значению;
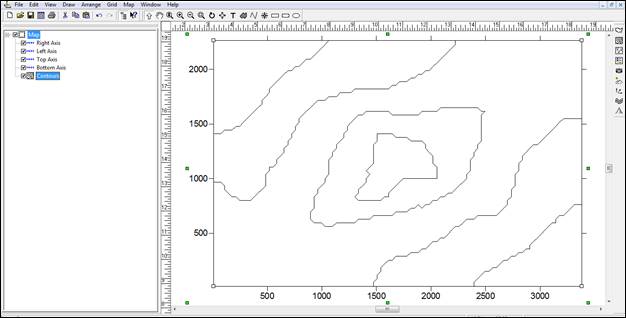
Рис. 33. Контурная карта созданная с помощью метода интерполяции Nearest Neighbor
-метод Nearest Neighbor спрямляет линии, слизкие к максимальному значению
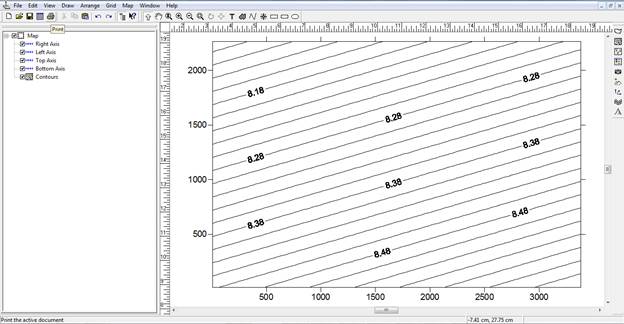
Рис. 34. Контурная карта созданная с помощью метода интерполяции Polynomial Regression, метод определения поверхности - Simple planar surface
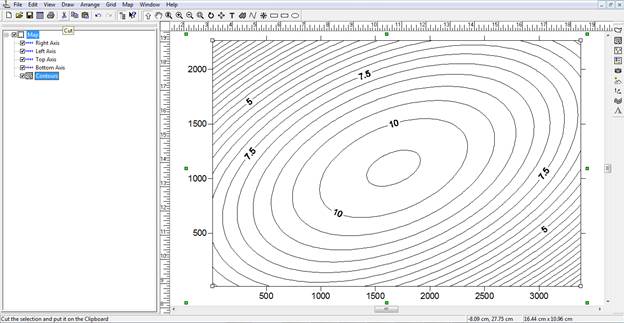
Рис. 35. Контурная карта созданная с помощью метода интерполяции Polynomial Regression, метод определения поверхности - Quadratic surface
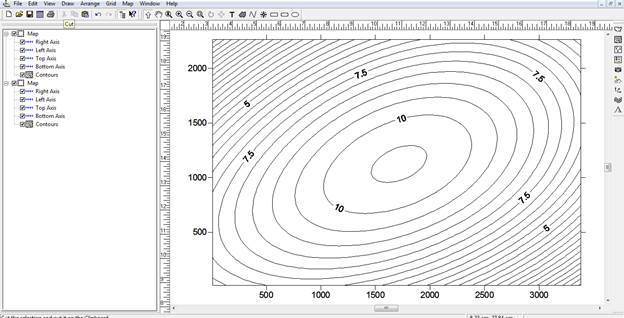
Рис. 36. Контурная карта созданная с помощью метода интерполяции Polynomial Regression, метод определения поверхности - Cubic surface
- использование методов Polynomial Regression позволяет построить карту, отражающую плотность и направление линий; в зависимости от выбранного метода определения поверхности линии имеют разную кривизну;
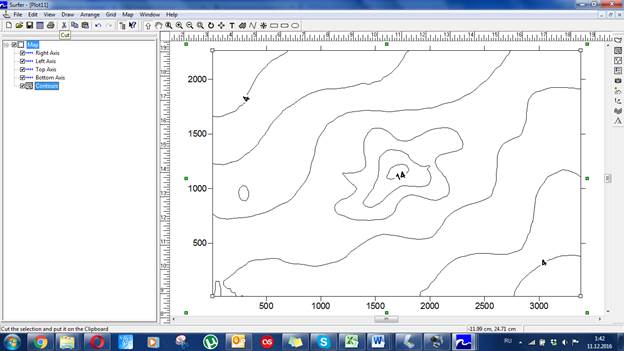
Рис. 37. Контурная карта созданная с помощью метода интерполяции Radial Basis Functions
-Метод Radial Basis Functions даёт карту, практически идентичную карте, получаемой с помощью метода Kriging
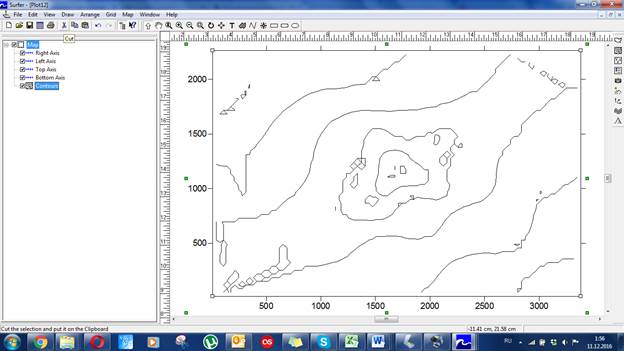
Рис. 38. Контурная карта созданная с помощью метода интерполяции Triangulation with Linear
-метод Triangulation with Linear даёт карту с большим количеством мелких структур.
