Обработка результатов экспериментов

СОДЕРЖАНИЕ

1. ПОСТАНОВКА ЗАДАЧИ.. 3

1.1 Выбор параметров оптимизации. 3

1.2 Выбор факторов. 3

1.3 Выбор области эксперимента. 3

1.4 Составление плана эксперимента [2] 4

1.5 Расчёт натуральных значений опытов. 4

1.6 Определение порядка реализации опытов чисел. 4

2. ВЫПОЛНЕНИЕ ОПЫТОВ.. 5

3. ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТОВ.. 6

3.1 Определение дисперсии воспроизводимости. 6

3.2. Вычисление коэффициентов уравнения регрессии[3] 6

3.3 Проверка статистической значимости. 7

3.3.1 Определение дисперсии коэффициентов уравнения. 7

3.3.2 Определение доверительного интервала. 8

3.4 Проверка адекватности модели. 8

3.4.1 Определение дисперсии адекватности. 8

3.4.2. Проверка гипотезы адекватности. 9

ЗАКЛЮЧЕНИЕ. 11

СПИСОК ЛИТЕРАТУРЫ.. 12

ПОСТАНОВКА ЗАДАЧИ

Вариант 6

Изучить влияние факторов алюминотермического способа восстановления Ме из фторида методом полного факторного эксперимента (ПФЭ) (типа 2^К).

Выбор параметров оптимизации

В качестве параметра оптимизации взять степень восстановления Ме(%).

Выбор факторов

В качестве факторов выбраны:

x₁ – количество восстановителя,%;

x₂ – температура процесса восстановления (t_пр),°С;

x₃ – продолжительность процесса восстановления, мин.

Выбор области эксперимента

Выбор области эксперимента произведен на основании априорных данных.

Выбранные интервалы варьирования факторов и их значения на нижнем и верхнем уровнях представлены в таблице 1.

Уровни факторов	Факторы
x1	x2	x3
Основной уровень
Интервал варьирования
Верхний уровень
Нижний уровень

Таблица 1. Значения уровней факторов

1.4 Составление плана эксперимента [2]

Для решения поставленной задачи используем ПФЭ типа 2^К. Для определения дисперсии воспроизводимости будет выполнено три параллельных опыта на основном (нулевом) уровне. Математическая модель будет представлена в виде неполного полинома второй степени. Матрица планирования представлена в таблице 2.

1.5 Расчёт натуральных значений опытов

Рассчитанные натуральные значения опытов представлены в таблице 2.

Определение порядка реализации опытов чисел

Порядок реализации опытов определяем по таблице случайных чисел.

Таблица 2. Матрица планирования ПФЭ 2³

№	Порядок реализации	Буквенное обозначен	Кодированные значения	Натуральные значения	y
х0	х1	х2	х3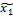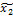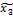
		abc	+	+	+	+				y1
		bc	+	-	+	+				y2
		ac	+	+	-	+				y3
		c	+	-	-	+				y4
		ab	+	+	+	-				y5
		b	+	-	+	-				y6
		a	+	+	-	-				y7
		(1)	+	-	-	-				y8

x₁ = a, x₂ = b, x₃ = c

ВЫПОЛНЕНИЕ ОПЫТОВ

Выполнение опытов производится согласно матрице планирования (таблица 2), согласно пункта 1.6 и выполнение параллельных опытов на основном уровне.

Полученные значения параметра оптимизации в параллельных опытах на основном уровне представлены в таблице 3.

Таблица 3. Значение ПО в параллельных опытах

№
yu	38,4	39,2	38,7

где, y_u - значение параметра в параллельных опытах на основном уровне;

u - номер параллельного опыта.

Условия опытов и результаты эксперимента представлены в таблице 4.

Таблица 4. Условия опытов и результаты эксперимента

№	Порядок реализации	Буквенное обозначение	Кодированные значения	y
х0	х1	х2	х3
		abc	+	+	+	+	76,2
		bc	+	-	+	+	60,0
		ac	+	+	-	+	35,5
		c	+	-	-	+	26,7
		ab	+	+	+	-	41,0
		b	+	-	+	-	35,1
		a	+	+	-	-	11,8
		(1)	+	-	-	-	9,5

ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТОВ