Интервальная оценка среднего квадратического отклонения

(с.к.о.)

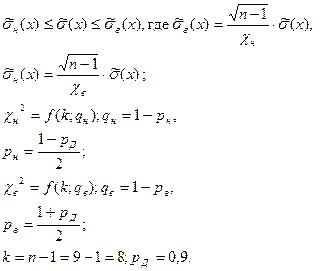
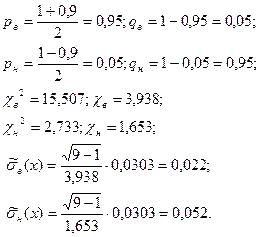
Результаты измерения

X= ± ;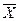

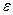Х = 8,80 ± 0,06 при p_Д= 0,95;

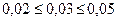при р_Д = 0,9;

Обработка результатов косвенных видов измерений

Исходные данные

Х₂: Результаты измерения длины металлического стержня (мм):

358.52; 358.51; 358.49; 358.48; 358.46; 358.45; 358.42; 358.59; 358.55; 358.53

X1	8.821	8.795	8.751	8.821	8.797	8.781	8.807	8.789	8.731
X2	358.52	358.51	358.49	358.48	358.46	358.45	358.42	358.59	358.55	358.53

Уравнение связи:

;

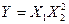Обработка результатов

Ранжированные результаты:

X1	8,731	8,751	8,781	8,789	8,795	8,797	8,807	8,821	8,821
X2	358,42	358,45	358,46	358,48	358,49	358,51	358,52	358,53	358,55	358,59

2.1. Методика обработки результатов измерений аргумента X2

Точечная оценка

1. Среднее арифметическое (оценка математического ожидания):

;

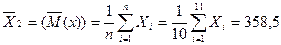2. Проверим правильность вычисления :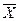

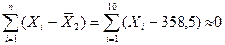, значит вычисления произведены, верно.

3. Найдем среднее квадратическое отклонение:

а) Оценка с.к.о. отдельного результата наблюдения (формула Бесселя):

;

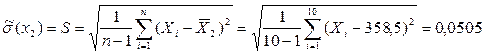б) Оценка с.к.о. среднего арифметического :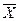

;

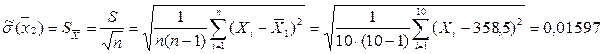Критерии грубых погрешностей

Так как количество измерений n=10, то используется критерий Грабса (Романовского или ν-критерий):

;

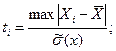
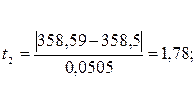
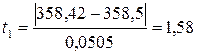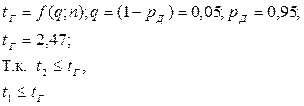
Не содержит грубых погрешностей, расчёт продолжаем.

Интервальная оценка

Оценка доверительного интервала математического ожидания :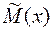
;

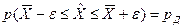По формуле Петерса:

;

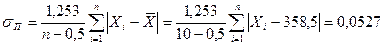Поскольку 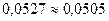, то это нормально распределение.

p_Д =0,95;

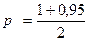= 0,975;

t = f ( p) = 1,96;

;

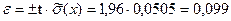Интервальная оценка среднего квадратического отклонения

(с.к.о.)

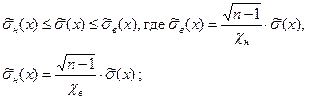
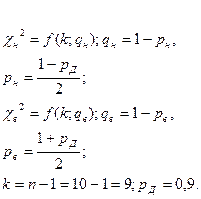
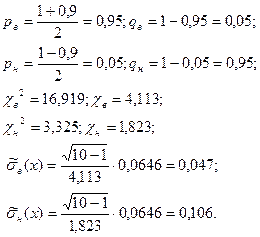
Результаты измерения

X = ± ;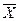

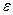X =358,5 ± 0,1; при p_Д = 0,95;

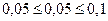; при р_Д=0,9;

Методика обработки косвенных видов измерений

1. Оценивается искомый результат, исходя из уравнения связи:

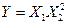= 8,788*358,5² = 1129453,53;

2. Находятся коэффициенты влияния :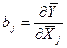

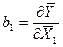= Х₂² = 128522,25;

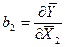= 2Х₁Х₂ = 6300,99;

3. Оценивается коэффициент корреляции между аргументами X1 и X:

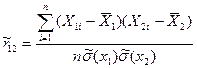, где n=min(n₁;n₂).

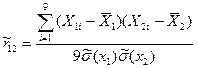= 0,586;

4. Оценка дисперсии искомого результата:

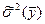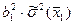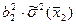= + +2 b₁ b₂ ;

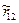
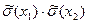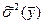= 3114235,25;

5. Находится эффективное число степеней свободы выборок двух аргументов X1 и X2:

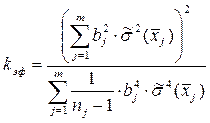= 20,88;

6. Определяется коэффициент Стьюдента

t_р = f (q, k_эф ); k_эф = 20; q = 0,05;

t_р = 2,09;

7. Оценка погрешности искомого результата

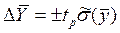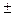= 2,09 1764,72 = 3688,26.

Результаты расчёта

;

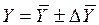Y = 1129453,53 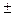3688,26; при р_Д = 0,95.

Методика расчёта статистических характеристик погрешностей СИ в эксплуатации. Определение класса точности

Исходные данные:

Р0, кг/м2	РМ, кг/cм2	РБ, кг/cм2	N, кг/cм2
9,0	8,97; 8,79; 8,88; 8,85; 8,92	9,15; 9,07; 9,01; 9,14; 9,02	15,0

Обработка результатов

1. Оценка систематической погрешности.

а) С учётом вариации:

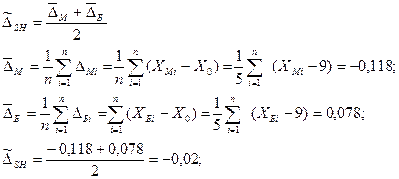
б) Без учёта вариации:

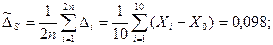
2. Оценка с.к.о.:

а) С учётом вариации:

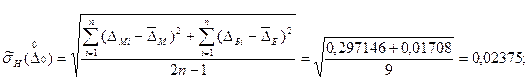
б) Без учета вариации:

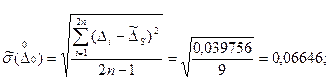
3. Оценка вариации:

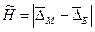=0,196.

4. Наибольшее значение основной погрешности:

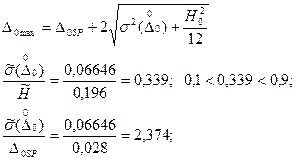
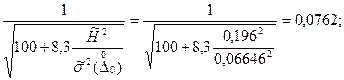
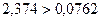, значит, нормируются обе составляющие случайной составляющей основной погрешности, а

.

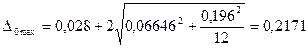5. Определение класса точности средства измерения:

Для аналоговых средств измерений класс точности нормируется пределом допускаемой основной приведённой погрешности:

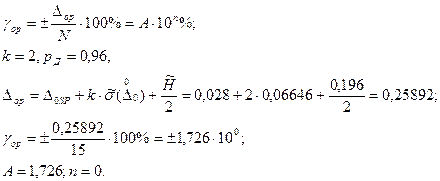
Результаты расчёта

Класс точности: А=2,0.

Приложение

Таблица П.1 - Значения нормированной функции Лапласа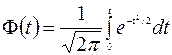

0,0	0,00000
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9

Примечание. Значения Ф(t) при t = 3,0 ÷ 4,5 следующие:

3,0	………...	0,49865	3,4	………...	0,49966	3,8	………...	0,49993
3,1	………...	0,49903	3,5	………...	0,49977	3,9	………...	0,49995
3,2	………...	0,49931	3,6	………...	0,49984	4,0	………...	0,499968
3,3	………...	0,49952	3,7	………...	0,49989	4,5	………...	0,499999

Таблица П.2 - Значения χ² - распределения Пирсона c² = f (q; k)

Число степеней свободы k = n – 1	Уровень значимости q, %
	0,00016	0,00063	0,00393	0,0158	0,0642	0,148	0,455
	0,0201	0,0404	0,103	0,211	0,446	0,713	1,386
	0,115	0,185	0,352	0,584	1,005	1,424	2,366
	0,297	0,429	0,711	1,064	1,649	2,195	3,357
	0,554	0,752	1,145	1,610	2,343	3,000	4,351
	0,872	1,134	1,635	2,204	3,070	3,828	5,348
	1,239	1,564	2,167	2,833	3,822	4,671	6,346
	1,646	2,032	2,733	3,490	4,594	5,527	7,344
	2,088	2,532	3,325	4,168	5,380	6,393	8,343
	2,558	3,059	3,940	4,865	6,179	7,267	9,342
	3,053	3,609	4,575	5,578	6,989	8,148	10,341
	3,571	4,178	5,226	6,304	7,807	9,034	11,340
	4,107	4,765	5,892	7,042	8,634	9,926	12,340
	4,660	5,368	6,571	7,790	9,467	10,821	13,339
	5,229	5,985	7,261	8,547	10,307	11,721	14,339
	5,812	6,614	7,962	9,312	11,152	12,624	15,338
	6,408	7,255	8,672	10,085	12,002	13,531	16,338
	7,015	7,906	9,390	10,865	12,857	14,440	17,338
	7,633	8,567	10,117	11,651	13,716	15,352	18,338
	8,260	9,237	10,851	12,443	14,578	16,266	19,337
	8,897	9,915	11,591	13,240	15,445	17,182	20,337
	9,542	10,600	12,338	14,041	16,314	18,101	21,337
	10,196	11,293	13,091	14,848	17,187	19,021	22,337
	10,856	11,992	13,848	15,659	18,062	19,943	23,337
	11,524	12,697	14,611	16,473	18,940	20,867	24,337
	12,198	13,409	15,379	17,292	19,820	21,792	25,336
	12,879	14,125	16,151	18,114	20,703	22,719	26,336
	13,565	14,847	16,928	18,939	21,588	23,647	27,336
	14,256	15,574	17,708	19,768	22,475	24,577	28,336
	14,953	16,306	18,493	20,599	23,364	25,508	29,336
Число степеней свободы k = n – 1	Уровень значимости q, %
						0,5
	1,074	1,642	2,706	3,841	5,412	6,635	7,879
	2,408	3,219	4,605	5,991	7,824	9,210	10,597
	3,665	4,642	6,251	7,815	9,837	11,345	12,838
	4,878	5,989	7,779	9,488	11,668	13,277	14,860
	6,064	7,289	9,236	11,070	13,388	15,086	16,750
	7,231	8,558	10,645	12,592	15,033	16,812	18,548
	8,383	9,803	12,017	14,067	16,622	18,475	20,278
	9,524	11,030	13,362	15,507	18,168	20,090	21,955
	10,656	12,242	14,684	16,919	19,679	21,666	23,589
	11,781	13,442	15,987	18,307	21,161	23,209	25,188
	12,899	14,631	17,275	19,675	22,618	24,725	26,757
	14,011	15,812	18,549	21,026	24,054	26,217	28,300
	15,119	16,985	19,812	22,362	25,472	27,688	29,819
	16,222	18,151	21,064	23,685	26,873	29,141	31,319
	17,322	19,311	22,307	24,996	28,259	30,578	32,801
	18,418	20,465	23,542	26,296	29,633	32,000	34,267
	19,511	21,615	24,769	27,587	30,995	33,409	35,718
	20,601	22,760	25,989	28,869	32,346	34,805	37,156
	21,689	23,900	27,204	30,144	33,687	36,191	38,582
	22,775	25,038	28,412	31,410	35,020	37,566	39,997
	23,858	26,171	29,615	32,671	36,343	38,932	41,401
	24,939	27,301	30,813	33,924	37,659	40,289	42,796
	26,018	28,429	32,007	35,172	38,968	41,638	44,181
	27,096	29,553	33,196	36,415	40,270	42,980	45,558
	28,172	30,675	34,382	37,652	41,566	44,314	46,928
	29,246	31,795	35,563	38,885	42,856	45,642	48,290
	30,319	32,912	36,741	40,113.	44,140	46,963	49,645
	31,391	34,027	37,916	41,337	45,419	48,278	50,993
	32,461	35,139	39,087	42,557	46,693	49,588	52,336
	33,530	36,250	40,256	43,773	47,962	50,892	53,672

Таблица П.3 - Значения q-процентных точек распределения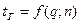

Число наблюдений	Уровень значимости q, %
0,1	0,5
	1,414	1,414	1,414	1,414	1,412
	1,732	1,730	1,728	1,710	1,689
	1,994	1,982	1,972	1,917	1,869
	2,212	2,183	2,161	2,067	1,996
	2,395	2,344	2,310	2,182	2,093
	2,547	2,476	2,431	2,273	2,172
	2,677	2,586	2,532	2,349	2,238
	2,788	2,680	2,616	2,414	2,294
	2,884	2,760	2,689	2,470	2,343
	2,969	2,830	2,753	2,519	2,387
	3,044	2,892	2,809	2,563	2,426
	3,111	2,947	2,859	2,602	2,461
	3,171	2,997	2,905	2,638	2,494
	3,225	3,042	2,946	2,670	2,523
	3,274	3,083	2,983	2,701	2,551
	3,320	3,120	3,017	2,728	2,577
	3,361	3,155	3,049	2,754	2,601
	3,400	3,187	3,079	2,779	2,623
	3,436	3,217	3,106	2,801	2,644
	3,469	3,245	3,132	2,823	2,664
	3,500	3,271	3,156	2,843	2,683
	3,529	3,295	3,179	2,862	2,701
	3,556	3,318	3,200	2,880	2,718
	3,582	3,340	3,220	2,897	2,734
	3,606	3,360	3,239	2,913	2,749
	3,629	3,380	3,258	2,929	2,764
	3,651	3,399	3,275	2,944	2,778
	3,672	3,416	3,291	2,958	2,792
	3,692	3,433	3,307	2,972	2,805
	3,711	3,449	3,322	2,985	2,818
	3,729	3,465	3,337	2,998	2,830
	3,746	3,480	3,351	3,010	2,842
	3,762	3,494	3,364	3,022	2,853
	3,778	3,507	3,377	3,033	2,864
	3,793	3,521	3,389	3,044	2,874
	3,808	3,533	3,401	3,055	2,885
	3,822	3,545	3,413	3,065	2,894
	3,835	3,557	3,424	3,075	2,904
	3,848	3,568	3,435	3,084	2,913
	3,861	3,579	3,445	3,094	2,922
Число наблюдений	Уровень значимости q, %
0,1	0,5
	3,873	3,590	3,455	3,103	2,931
	3,885	3,600	3,465	3,112	2,940
	3,896	3,610	3,474	3,120	2,948
	3,907	3,620	3,483	3,129	2,956
	3,918	3,630	3,492	3,137	2,964
	3,928	3,639	3,501	3,145	2,972
	3,938	3,648	3,510	3,152	2,980
	3,948	3,656	3,518	3,160	2,987
	3,957	3,665	3,526	3,167	2,994
	3,966	3,673	3,534	3,175	3,201

Таблица П.4 - Распределение Стьюдента t_p = f (q; k)

Число степеней свободы k	Уровень значимости q = (1 – PД)×100, %
	6,31	12,71	63,66
	2,92	4,30	9,92
	2,35	3,18	5,84
	2,13	2,78	4,60
	2,02	2,57	4,03
	1,94	2,45	3,71
	1,90	2,36	3,50
	1,86	2,31	3,36
	1,83	2,26	3,25
	1,81	2,23	3,17
	1,78	2,18	3,06-
	1,76	2,14	2,98
	1,75	2,12	2,92
	1,73	2,10	2,88
	1,72	2,09	2,84
	1,72	2,07	2,82
	1,71	2,06	2,80
	1,71	2,06	2,78
	1,70	2,05	2,76
	1,70	2,04	2,75
¥	1,64	1,96	2,58