Главные радиусы кривизны

Через любую точку поверхности Q эллипсоида можно провести множество нормальных сечений. Каждое из них имеет свою кривизну. Среди всего семейства нормальных сечений существуют два таких, для которых одно имеет наибольшую кривизну, а другое – наименьшую. Эти два сечения называют главными нормальными сечениями, а их радиусы кривизны – главными радиусами кривизны.

Главные нормальные сечения лежат на взаимно ортогональных плоскостях. На эллипсоиде главными нормальными сечениями являются - меридиан (РР₁) и первый вертикал (ТТ₁).

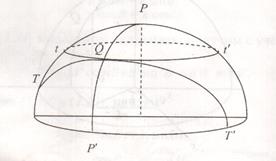При этом первый вертикал и параллель (ТТ¹) в точке Q имеют общую касательную, поскольку обе линии перпендикулярны к меридиану.

Приняты обозначения: M – радиус кривизны меридиана и N – радиус кривизны первого вертикала (не отождествлять с радиусом кривизны параллели !).

Из всего семейства параллелей только экватор является главным нормальным сечением.

Для любой кривой дифференциал ее дуги равен произведению радиуса кривизны и дифференциала угла между касательными к кривой в конечных точках этой элементарной дуги:

dX= М dB.

Поэтому имеем:

М = dX/dB = a(1 – e²) / W³ = с / V³ = р / W³.

Очевидно, что на полюсе М_п = с (полярный радиус кривизны), а на экваторе - М_э = р = b²/ a (с - всегда больше р).

Для радиуса кривизны первого вертикала имеет место выражение: N = dy/dL = а / W = c/V = a / (1 – e²sin²B)^1/2

Связь значений главных радиусов кривизны:

Используя выражения М = с / V³ и N = c/V, получим:

N / M = V².

Во всех точках поверхности эллипсоида, кроме полюсов, N> M. На полюсе (В=90⁰) M=N = c.

Используя выражения для M и N, получим

(N – M) / M = η² = (е¹)² cos²B - величина, характеризует отступление поверхности эллипсоида в данной точке от сферической поверхности (на полюсах ).

На полюсах η²= 0 , к экватору η² примерно 1/ 150.

Для решения многих задач часто вычисляютсреднее

значение радиуса кривизны как:R = √ MN.

Лекция 4: Длины дуг координатных линий

(меридиана и параллели)

Длина дуги меридиана.

Из математики известно, что длина ds элементарной дуги произвольной плоской кривой определится как ds =ρα,

где ρ –радиус кривизны в начальной точке; α –угол в радианах между нормалями в начальной и конечной точках. Тогда для дуги меридиана Х в общем виде будем иметь:

dX = MdBили

_B2

Х = ∫_B1 MdB.

Следует заметить, что представленный интеграл относится к классу эллиптических интегралов и в элементарных функциях не выражается (здесь М также зависит от В).

Известны несколько способов приближенноговычисления данного вида интеграла, когда ΔВ не превышает 5⁰.

В₂

C погрешностью не более 0,0001 минтегралdX =∫_B1 MdBможно решить после изменения пределов интегрирования: от В₀ = 0⁰ до Вi, т.е. от плоскости экватора до точки с широтой Вi, предварительно представив его выражение в виде достаточно простого ряда:

Х_i = а₀В_i –( а₂/2) sin2B_i +(a₄/4) sin4B_i –(a₆/6) sin6B_i + …,

где численные значения коэффициентов «а_i» зависят от значений

большой полуоси и первого эксцентриситета эллипсоида:

а₀ = m₀ +m₂/2 +3/8 m₄, где m₀ = a (1 – e²),

a₂ = m₂/2 + m₄/2 + 15/32 m₆,_, m₂ = 3/2 e² m₀,

a₄ = m₄/8 + 3/16 m₆, m₄ = 5/4 e² m₂,

a₆ = m₆/32, m₆ = 7/6 e² m₄,

где а –значение большой полуоси эллипсоида;

е – значение первого эксцентриситета.

Так, например, для эллипсоида Красовского коэффициенты принимают значения:

а₀ = 6 367 558,497 м; а₂ = 32 072,960 м; а₄ =67,312 м;а₆ = 0,132 м.

Для определения длины дуги меридиана ∆Х между точками с широтами В₁ и В₂ используется выражение:

∆Х = Х₂ - Х₁.

Для определения длины дуги с погрешностью 1-2 см применяют формулу Симпсона, основанную на методе численного интегрирования:

∆Х = ∆В / 6 (М₁ +4 М _СР+ М_{2 .}),

где М_i – значение радиусов кривизны меридиана в точках с В₁, В_ср и В _2..

Значение М_i удобно вычислять по формулам:

a(1 – e²)

M = c / V³ или М = --------------------.

(1 – e²sin²B)^3/2

Во многих случаях достаточно знать длину дуги меридиана с погрешностью 1…2 м. С этой целью используется формула вида

∆Х = М_ср. ∆В.

При разности широт ∆В более 5⁰ (при ∆Х более 500 км) определение длины дуги выполняется в виде суммы двух и более дуг с равенством разностей широт до 5⁰.

При малых размерах ∆Х, например при определении рамок съемочной трапеции топографической карты, часто применяют

формулу со средними аргументами:

∆Х = М_ср. ∆В +( ∆В³/8) [ae²(1 –е²)cos2B_ср.].

При (ae² = 43 км) и масштабе карты 1: 50 000 (∆В = 10ʹ) второе слагаемое правой части составляет примерно 0,0004 м или 0,4 мм.

2. Длина дуги параллели. Параллель эллипсоида представляет собой окружность радиуса r = NcosB, где N – радиус кривизны первого вертикала. Тогда длина дуги такой окружности определяется как

∆Y = NcosB (∆L),

где NcosB = r – радиус параллели на широте В.

Очевидно, что длина дуги параллели при одном и том же значении ∆L на разных широтах различна и убывает при увеличении широты В.

Для вычисления значения радиуса кривизны первого вертикала можно применять формулу вида

N = dy/dL = а / W = c/V = a / (1 – e²sin²B)^1/2