Как решить однородное дифференциальное уравнение?

Однородные дифференциальные уравнения первого порядка

На данном уроке мы рассмотрим так называемые однородные дифференциальные уравнения первого порядка. Наряду с уравнениями с разделяющимися переменными и линейными неоднородными уравнениями этот тип ДУ встречается практически в любой контрольной работе по теме диффуров. Если Вы зашли на страничку с поисковика или не очень уверенно ориентируетесь в дифференциальных уравнениях, то сначала настоятельно рекомендую проработать вводный урок по теме – Дифференциальные уравнения первого порядка. Дело в том, что многие принципы решения однородных уравнений и используемые технические приемы будут точно такими же, как и для простейших уравнений с разделяющимися переменными.

В чём отличие однородных дифференциальных уравнений от других типов ДУ? Это проще всего сразу же пояснить на конкретном примере.

Пример 1

Решить дифференциальное уравнение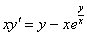

Решение:
Что в первую очередь следует проанализировать при решении любого дифференциального уравнения первого порядка? В первую очередь необходимо проверить, а нельзя ли сразу разделить переменные с помощью «школьных» действий? Обычно такой анализ проводят мысленно или пытаются разделить переменные на черновике.

В данном примере переменные разделить нельзя (можете попробовать поперекидывать слагаемые из части в часть, повыносить множители за скобки и т.д.). Кстати, в данном примере, тот факт, что переменные разделить нельзя, достаточно очевиден ввиду наличия множителя .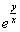

Возникает вопрос – как же решить этот диффур?

Нужно проверить, а не является ли данное уравнение однородным? Проверка несложная, и сам алгоритм проверки можно сформулировать так:

В исходное уравнение:

вместо 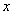подставляем 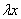, вместо 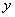подставляем 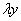, производную не трогаем:

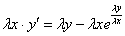
Буква лямбда – это некоторый абстрактный числовой параметр, дело не в самих лямбдах, и не в их значениях, а дело вот в чём:

Если в результате преобразований удастся сократить ВСЕ «лямбды» (т.е. получить исходное уравнение), то данное дифференциальное уравнение является однородным.

Очевидно, что лямбды сразу сокращаются в показателе степени:

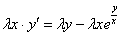
Теперь в правой части выносим лямбду за скобки:

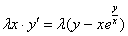
Обе части уравнения можно сократить на эту самую лямбду:

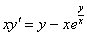
В результате все лямбды исчезли как сон, как утренний туман, и мы получили исходное уравнение.

Вывод: Данное уравнение является однородным

Поначалу рекомендую проводить рассмотренную проверку на черновике, хотя очень скоро она будет получаться и мысленно.

Как решить однородное дифференциальное уравнение?

У меня очень хорошая новость. Абсолютно все однородные уравнения можно решить с помощью одной-единственной (!) стандартной замены.

Функцию «игрек» необходимо заменить произведением некоторой функции 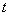(тоже зависящей от «икс») и «икса»:

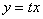
Выясняем, во что превратится производная 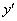при такой замене, используем правило дифференцирования произведения. Если 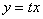, то:

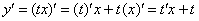
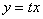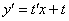Подставляем и в исходное уравнение :

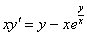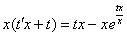
Что даст такая замена? После данной замены и проведенных упрощений мы гарантировано получим уравнение с разделяющимися переменными. Еще раз подчеркиваю, для ЛЮБОГО однородного уравнения нужно провести одну и ту же замену: строго 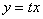и, соответственно, строго .

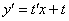После подстановки проводим максимальные упрощения уравнения:

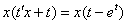
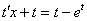
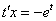
Далее алгоритм работает по накатанной колее уравнения с разделяющимися переменными.

Если 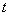– это функция, зависящая от «икс», то .
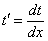Таким образом:

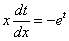
Разделяем переменные, при этом в левой части нужно собрать только «тэ», а в правой части – только «иксы»:

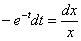
Переменные разделены, интегрируем:


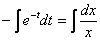
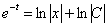
Согласно моему первому техническому совету из статьи Дифференциальные уравнения первого порядка константу во многих случаях целесообразно «оформить» в виде логарифма.

После того, как уравнение проинтегрировано, нужно провести обратную замену, она тоже стандартна и единственна:
Если 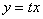, то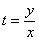
В данном случае: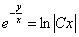

В 19-ти случаях из 20-ти решение однородного уравнения записывают в виде общего интеграла.

Ответ: общий интеграл: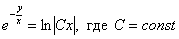

Почему почти всегда ответ однородного уравнения даётся в виде общего интеграла?
В большинстве случаев невозможно выразить «игрек» в явном виде (получить общее решение), а если и возможно, то чаще всего общее решение получается громоздким и ужасно корявым.

Так, например, в рассмотренном примере, общее решение получить можно:

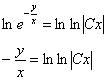
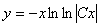– общее решение.
Ну, еще куда ни шло. Хотя, согласитесь, все равно кривовато смотрится.

Кстати, в данном примере я не совсем «прилично» записал общий интеграл. Это не ошибка, но в «хорошем» стиле, напоминаю, общий интеграл принято записывать в виде 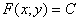. Для этого сразу после интегрирования уравнения, константу следует записать без всякого логарифма (вот и исключение из правила!):

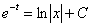
И после обратной замены получить общий интеграл в «классическом» виде:

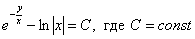
Полученный ответ можно проверить. Для этого нужно продифференцировать общий интеграл, то есть найти производную от функции, заданной неявно:

Избавляемся от дробей, умножая каждую часть уравнения на :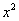

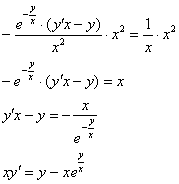
Получено исходное дифференциальное уравнение, значит, решение найдено правильно.

Желательно всегда проводить проверку. Но однородные уравнения неприятны тем, что проверять их общие интегралы обычно трудно – для этого необходима весьма и весьма приличная техника дифференцирования. В рассмотренном примере в ходе проверки уже пришлось находить не самые простые производные (хотя сам по себе пример достаточно простой). Если сможете проверить – проверяйте!

Пример 2

Проверить уравнение на однородность и найти его общий интеграл. Выполнить проверку.

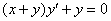
Это пример для самостоятельного решения, мой ответ в конце урока максимально упрощен, а сам общий интеграл представлен в виде 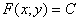. Напоминаю, что если у вас получится ответ в иной записи, то это еще не значит, что вы допустили ошибку.

Не правда ли простой пример? Внешний вид диффуров очень обманчив ;-) И да, в решении появилась важная тема, которую мы серьёзно разовьём к экватору урока.

Пример 3

Решить дифференциальное уравнение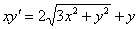

Решение: проверим уравнение на однородность, для этого в исходное уравнение вместо 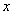подставим 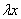, а вместо 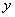подставим :

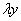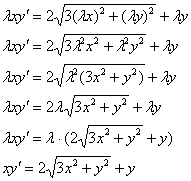
Все лямбды сократились, и получилось исходное уравнение, значит, данное ДУ является однородным.

Проведем стандартную замену:

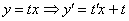
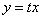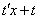Подставим и в исходное уравнение:

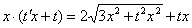
После подстановки результат стремимся максимально упростить:

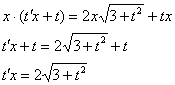
Разделяем переменные и интегрируем:

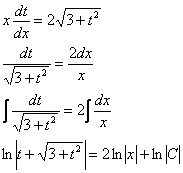
Общий интеграл получен, теперь его нужно довести его до ума.Перед тем как выполнять обратную замену 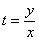, рекомендую снова максимально упростить полученное выражение. Об этом я уже упомянул в решении Примера №2.

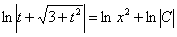
Возможно, у некоторых возник вопрос, почему я иногда вдруг убираю модуль под логарифмом? Причина проста – выражение под знаком логарифма, в данном случае 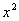, неотрицательно, а значит, модуль записывать не обязательно.

Упрощаем дальше:

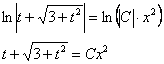
Вот теперь обратная замена: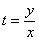

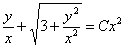
Под корнем нужно привести слагаемые к общему знаменателю и вынести из-под корня всё, что можно. Эти действия часто приходится выполнять в ходе решения однородного уравнения, запомните их:

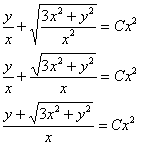
Ответ: общий интеграл: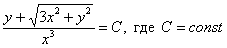

Я выполнил проверку общего интеграла, но приводить её не буду, а то вы больше не придёте к такому маньяку. Попробуйте для интереса найти производную. Времяпровождение получите из разряда тех, о которых долго вспоминают. И гордятся.

Пример 4

Выполнить проверку на однородность и решить дифференциальное уравнение

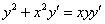
Вот здесь проверка общего интеграла будет не очень сложной. Полное решение и ответ в конце урока.

Рассмотрим пару примеров, когда однородное уравнение задано с готовыми дифференциалами.

Пример 5

Решить дифференциальное уравнение

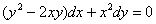
Решениебудем привыкать оформлять компактнее. В чистовом оформлении работы не обязательно выполнять проверку на однородность. На чистовике она гораздо чаще не проводится, чем проводится. Проверка делается на черновике или мысленно, а если вы прорешали первые 4 примера, то многие из вас однородные уравнения уже узнают «в лицо».

Таким образом, почти всегда решение начинается с записи: «Данное уравнение является однородным, проведем замену: …».

Но вернемся к нашему уравнению. В нём присутствуют дифференциалы 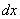и 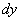. Уравнение можно решить и с дифференциалами, но алгоритм решения будет немного другой, более того, значительно увеличится риск путаницы и ошибок.

Поэтому, если однородное уравнение дано в дифференциалах, то сначала я рекомендую выразить производную 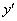, а дальше использовать уже накатанную схему решения.

Для того чтобы выразить производную, нужно каждое слагаемое разделить на :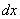

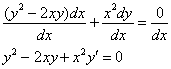
Вот так-то лучше и понятнее.

Теперь коснёмся одного момента, который вы уже заметили в ходе решения 2-го и 4-го примеров. В дифференциальных уравнениях (и особенно это типично для однородных ДУ) некоторые решения «лежат на поверхности». Чаще всего, это очевидное решение 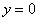. Подставим 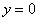и и её производную 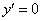в наше уравнение (что легко сделать и устно):

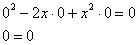
Получено верное равенство, значит, функция 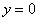является решением уравнения и этот факт желательно отметить при оформлении задачи. Зачем? В ходе дальнейших преобразований существует риск потерять данное решение, то есть оно может не войти в общий интеграл, как это, например, случилось в Примере №4.

Дальше всё тривиально, проведем замену: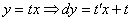

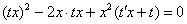
После подстановки максимально упрощаем уравнение:

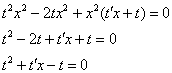
Разделяем переменные:

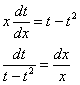
Интегрируем:

Интеграл левой части стандартно решается с помощью выделения полного квадрата, но в диффурах гораздо удобнее использовать метод неопределенных коэффициентов:

Используя метод неопределенных коэффициентов, разложим подынтегральную функцию в сумму элементарных дробей:


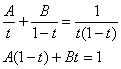
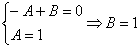
Таким образом: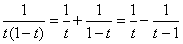

Находим интегралы:

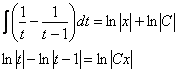
Перед обратной заменой в новорожденном общем интеграле опять упрощаем всё, что можно упростить:

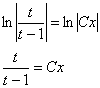
Вот теперь обратная замена :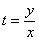

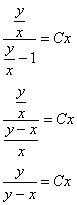
Ответ: общий интеграл: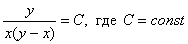

Найденное и отмеченное ранее решение 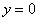входит в общий интеграл при нулевом значении константы (опять же легко проверяется устно), поэтому его не нужно дополнительно записывать в ответ.

Кстати редкий случай, когда общее решение однородного ДУ выражается в более или менее «приличном» виде:

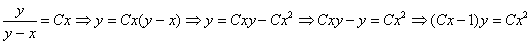
Ответ: общее решение: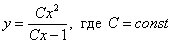

Но это уже понты, после чего преподаватель с удовольствием предложит вам задание повышенной сложности, которое вы будете решать до конца семестра. Было бы хорошей шуткой, если бы не было горьким опытом.

Попробуйте выполнить проверку общего решения, здесь она не сверхсложная.