Абсолютная и относительная погрешности вычислений
Абсолютная погрешность вычисленийнаходится по формуле:
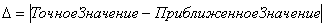
Знак модуля показывает, что нам без разницы, какое значение больше, а какое меньше. Важно, насколько далеко приближенный результат отклонился от точного значения в ту или иную сторону.
Относительная погрешность вычисленийнаходится по формуле:
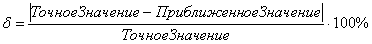 , или, то же самое:
, или, то же самое:
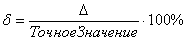
Относительная погрешность показывает, на сколько процентов приближенный результат отклонился от точного значения. Существует версия формулы и без умножения на 100%, но на практике почти всегда используют вышеприведенный вариант с процентами.
После короткой справки вернемся к нашей задаче, в которой мы вычислили приближенное значение функции 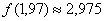 с помощью дифференциала.
с помощью дифференциала.
Вычислим точное значение функции с помощью микрокалькулятора:
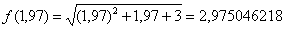 , строго говоря, значение всё равно приближенное, но мы будем считать его точным. Такие уж задачи встречаются.
, строго говоря, значение всё равно приближенное, но мы будем считать его точным. Такие уж задачи встречаются.
Вычислим абсолютную погрешность:
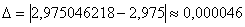
Вычислим относительную погрешность:
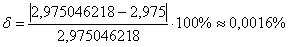 , получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение.
, получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение.
Ответ: 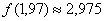 , абсолютная погрешность вычислений
, абсолютная погрешность вычислений 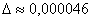 , относительная погрешность вычислений
, относительная погрешность вычислений 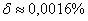 .
.
Следующий пример для самостоятельного решения:
Пример 4
Вычислить приближенно с помощью дифференциала значение функции 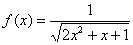 в точке
в точке 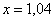 . Вычислить более точное значение функции в данной точке, оценить абсолютную и относительную погрешность вычислений.
. Вычислить более точное значение функции в данной точке, оценить абсолютную и относительную погрешность вычислений.
Примерный образец чистового оформления и ответ в конце урока.
Многие обратили внимание, что во всех рассмотренных примерах фигурируют корни. Это не случайно, в большинстве случаев в рассматриваемой задаче действительно предлагаются функции с корнями.
Но для страждущих читателей я раскопал небольшой пример с арксинусом:
Пример 5
Вычислить приближенно с помощью дифференциала значение функции 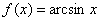 ; в точке
; в точке 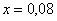 .
.
Этот коротенький, но познавательный пример тоже для самостоятельного решения.
Теперь рассмотрим особое задание:
Пример 6
Вычислить приближенно с помощью дифференциала 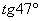 , результат округлить до двух знаков после запятой.
, результат округлить до двух знаков после запятой.
Решение:Что нового в задании? По условию требуется округлить результат до двух знаков после запятой. Но дело не в этом, школьная задача округления, думаю, не представляет для вас сложностей. Дело в том, что у нас дан тангенс с аргументом, который выражен в градусах.
Что делать, когда вам предлагается для решения тригонометрическая функция с градусами? Например, 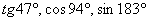 и т. д.
и т. д.
Алгоритм решения принципиально сохраняется, то есть необходимо, как и в предыдущих примерах, применить формулу 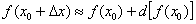
Записываем очевидную функцию 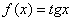
Значение 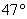 нужно представить в виде
нужно представить в виде 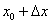 . Серьёзную помощь окажет таблица значений тригонометрических функций. Кстати, кто её не распечатал, рекомендую это сделать, поскольку заглядывать туда придется на протяжении всего курса изучения высшей математики.
. Серьёзную помощь окажет таблица значений тригонометрических функций. Кстати, кто её не распечатал, рекомендую это сделать, поскольку заглядывать туда придется на протяжении всего курса изучения высшей математики.
Анализируя таблицу, замечаем «хорошее» значение тангенса, которое близко располагается к 47 градусам, а именно: 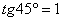 . Таким образом:
. Таким образом: 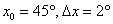 .
.
После предварительного анализа градусы необходимо перевести в радианы. Так, и только так!
В данном примере непосредственно из тригонометрической таблицы можно выяснить, что 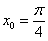 . По формуле перевода градусов в радианы:
. По формуле перевода градусов в радианы: 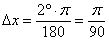 (формулы можно найти в той же таблице). Дальнейшее шаблонно:
(формулы можно найти в той же таблице). Дальнейшее шаблонно:
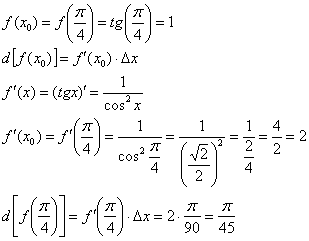 .
.
Таким образом: 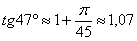 (при вычислениях используем значение
(при вычислениях используем значение 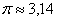 ). Результат, как и требовалось по условию, округлён до двух знаков после запятой.
). Результат, как и требовалось по условию, округлён до двух знаков после запятой.
Ответ: 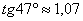 .
.
Пример 7
Вычислить приближенно с помощью дифференциала 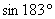 , результат округлить до трёх знаков после запятой.
, результат округлить до трёх знаков после запятой.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Как видите, ничего сложного, градусы переводим в радианы и придерживаемся обычного алгоритма решения.
