Упражнения на «чтение» уравнения гармонических колебаний
1 Зависимость координаты колеблющейся точки от времени имеет вид x = A sin (pt/12). Известно, что в момент времени t = 10 с смещение равно
6 мм. Определите амплитуду колебаний (в мм).
2 Пружинный маятник совершает колебания, уравнение которых x = 4 cos(pt+ p/3) (см). Определите скорость и ускорение маятника через 20 с после начала движения. Масса маятника 200 г.
3 Через сколько секунд от начала движения точка, совершающая колебания по закону x = A sin wt, сместится от положения равновесия на половину амплитуды? Период колебаний равен 36 с.
4 Математическому маятнику в положении равновесия сообщили некоторую скорость, и за 1/4 с она уменьшилась в 2 раза. Найдите длину маятника, считая возникшие колебания гармоническими.
5 Груза, подвешенного на пружине, в зависимости от времени задается законом x = 8 cos (10t + p/4). При этом максимальная кинетическая энергия груза равна 0,8 Дж. Найдите жесткость пружины.
2 Упражнения на составление уравнения движения тела, совершающего гармонические колебания
1 Напишите уравнение гармонических колебаний груза массой m = 100г, подвешенного на пружине жесткостью k = 10Н/м, если амплитуда колебаний A = 30мм, а начальная фаза j0 = p/4.
2 В начальный момент времени смещение частицы x0 = 1,7см, а скорость v0Х = -1 м/с. Масса частицы m = 0,4кг, ее полная энергия
W = 800мДж. Напишите закон колебаний частицы и определите путь, пройденный частицей за время t=0,1pс.
3 Грузик массой m = 200г , прикрепленный к горизонтальной пружине жесткостью k = 20 Н/м, покоится на гладкой горизонтальной плоскости. Второй конец пружины закреплен. Грузику толчком сообщили горизонтальную скорость v0 = 0,98 м/с, направленную вдоль оси пружины. Определите закон движения грузика x(t), считая, что направление начальной скорости совпадает с положительным направлением оси ОХ.
4 Грузик массой m = 200 г подвешен на вертикальной пружине жесткости k = 20 Н/м. Его удерживают таким образом, что пружина остается недеформированной. В начальный момент времени груз освобождают, не сообщая ему начальной скорости. Определите закон движения грузика x(t), считая, что ось ОХ направлена вертикально вниз, а значение координаты
х =0 соответствует положению нижнего конца недеформированной пружины.
3 Упражнения на использование связи между максимальными значениями смещения, скорости и ускорения
1 Гирька массой 0,3 кг, подвешенная на пружине жесткостью 15 Н/м, колеблется так, что ее максимальная скорость равна 2,8 см/с. Найдите амплитуду колебаний. Силами сопротивления пренебречь.
2 Максимальная скорость математического маятника при малых колебаниях vmax=5 см/с, период колебаний Т = 1 с. Определите максимальный угол отклонения маятника от вертикали в процессе колебаний.
3 Шарик массой 50 г, подвешенный на пружине, совершает гармонические колебания с амплитудой 10 см. Чему равна максимальная величина возвращающей силы (в мН), действующей на шарик, если циклическая частота колебаний 4 с-1.
4 Точка совершает гармонические колебания вдоль прямой линии. При движении между крайними положениями средняя скорость оказалась равной v = 4 м/с. Найдите максимальную скорость.
5 Небольшое тело совершает гармонические колебания. Зная, что его максимальная скорость vmax = 9,42 м/с, найдите величину средней скорости тела за время, в течение которого оно перемещается из одного крайнего положения в другое.
Тест № 1 «Характеристики колебательного движения»
1 Составьте правильное утверждение
Свободные колебания – это колебания, происходящие под действием…
А) силы тяжести;
Б) силы упругости;
В) внутренней силы, возникающей в системе при выведении ее из положения равновесия;
Г) внешней периодически меняющейся силы.
2 Какое из перечисленных колебаний является свободным?
1) Колебание груза, подвешенного на нити, один раз отведенного от положения равновесия и отпущенного.
2) Колебание качелей, раскачиваемых человеком, стоящим на поверхности земли.
А) Только 1; Б) Только 2; В) и 1, и 2; Г) ни 1, ни 2.
3 Укажите тела, совершающие гармонические колебания
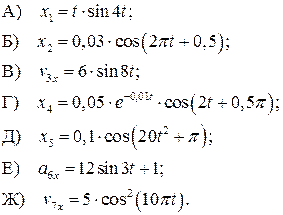
4 Продолжите утверждение
Гармонические колебания возникают в системе, если при выведении ее из положения равновесия появляется…
А) сила упругости, направленная к положению равновесия;
Б) сила тяжести и сила упругости, равнодействующая которых направлена к положению равновесия;
В) сила, направленная к положению равновесия, модуль которой прямо пропорционален координате тела. Такая сила называется квазиупругой.
5 Составьте правильные утверждения
| Период колебаний – это… | |
| Частота колебаний – это.. |
А) Время, в течение которого тело совершает колебательное движение;
Б) Число колебаний за определенное время;
В) Число колебаний за один период;
Г) Время, за которое тело совершает одно полное колебание;
Д) Число колебаний в единицу времени.
6 Какая часть периода требуется для того, чтобы тело, совершающее гармонические колебания, из положения равновесия первый раз пришло в крайнее положение?
А) 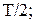 Б)
Б) 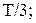 В)
В) 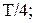 Г)
Г) 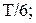 Д)
Д) 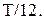
7 Выберите правильное утверждение.
Амплитуда колебаний – это…
А) путь, который проходит тело за период;
Б) расстояние между двумя крайними положениями колеблющегося тела;
В) максимальное растяжение пружины;
Г) максимальное отклонение тела от положения равновесия.
8 Составьте правильное утверждение
Циклическая частота – это …
А) время полного колебания;
Б) число колебаний за определенное время;
В) число колебаний за 2π секунды;
Г) число колебаний в единицу времени.
Циклическая частота связана с обычной частотой соотношением …
А) 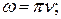 Б)
Б) 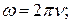 В)
В) 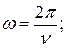 Г)
Г) 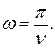
Циклическая частота зависит от …
А) размаха колебаний;
Б) энергии, сообщенной системе при выведении ее из положения равновесии;
В) параметров самой колебательной системы;
Г) способа выведения колебательной системы из положения равновесия.
9 Тело совершает гармонические колебания по закону 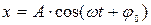 . Что называют фазой колебания?
. Что называют фазой колебания?
А) A; Б) 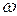 ; В)
; В) 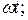 Г)
Г) 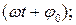 Д)
Д) 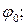 Е)
Е) 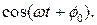
10 За 5 секунд материальная точка совершает 10 гармонических колебаний. Чему равны частота и период колебаний?
А) T = 0,5 с, ν = 2 Гц ; Б) T = 2 с, ν = 0,5 Гц;
В) T = 50 с, ν = 0,02 Гц ; Г) T = 0,02 с, ν = 50 Гц.
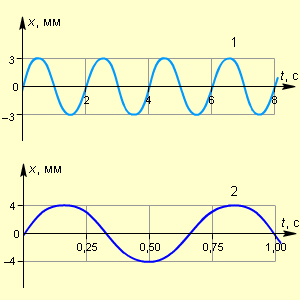
11 На рисунке представлены графики двух колебательных процессов: ось X – время в секундах, ось Y – координата в миллиметрах. Выберите колебание с: максимальной амплитудой и максимальной частотой.
А) Максимальная амплитуда и частота у тела 1;
Б) Максимальная амплитуда и частота у тела 2;
В) Максимальная амплитуда – тело 1;
Максимальная частота – тело 2;
Г) Максимальная амплитуда – тело 2;
Максимальная частота – тело 1.
12 Координата колеблющегося тела изменяется по закону 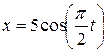 .
.
Чему равна частота колебаний? Все величины выражены в единицах СИ.
А) ¼ Гц; Б) 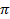 /2 Гц; В) 2 Гц; Г) 4 Гц.
/2 Гц; В) 2 Гц; Г) 4 Гц.
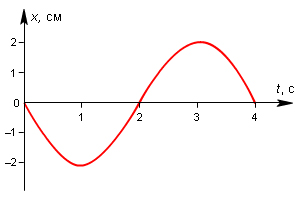 13 На рисунке показана зависимость координаты колеблющейся точки от времени. Чему равна частота колебаний скорости данной материальной точки?
13 На рисунке показана зависимость координаты колеблющейся точки от времени. Чему равна частота колебаний скорости данной материальной точки?
А) 4 Гц; Б) 2 Гц;
В) 0,5 Гц ; Г) 0,25 Гц.
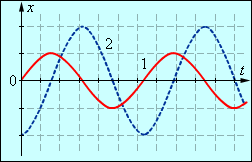 14 Два тела привели в колебательное движение. Зависимости координат тел от времени показаны на рисунке. Каким образом тела привели в колебательное движение?
14 Два тела привели в колебательное движение. Зависимости координат тел от времени показаны на рисунке. Каким образом тела привели в колебательное движение?
А) Оба тела отклонили от положения равновесия и отпустили без начальной скорости;
Б) Оба тела отклонили от положения равновесия и толчком сообщили скорость;
В) Первое тело толкнули в положении равновесия, второе тело отклонили от положения равновесия и отпустили;
Г) Второе тело толкнули в положении равновесия, первое тело отклонили от положения равновесия и отпустили.
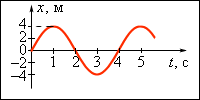 15 Какое из уравнений описывает гармонические колебания, изображенные на рисунке?
15 Какое из уравнений описывает гармонические колебания, изображенные на рисунке?
А) 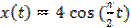 ; Б)
; Б) 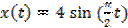 ;
;
В) 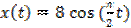 ; Г)
; Г) 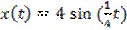 .
.
16 Три тела совершают гармонические колебания. Сравните фазы колебаний тел в производный момент времени.
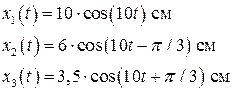
А) 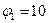 >
> 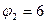 >
> 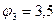 ;
;
Б) 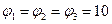 ;
;
Г) 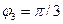 >
> 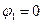 >
> 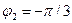 ;
;
Д) Третье тело опережает первое по фазе на 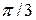 , второе тело отстает от первого по фазе на
, второе тело отстает от первого по фазе на 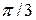 .
.
Тест № 2 «Период колебаний маятника»
1 Груз, прикрепленный к пружине, совершает гармонические колебания в горизонтальной плоскости. Как изменится период колебаний груза, если его массу увеличить в 3 раза, а жесткость пружины уменьшить в 3 раза?
А) Увеличится в 3 раза; Б) Уменьшится в 3 раза;
В) Увеличится в 9 раз; Г) Уменьшится в 9 раз;
Д) Не изменится.
2 Две пружины жесткостью k каждая соединили параллельно и подвесили к ним груз массой m. Чему равна циклическая частота колебаний груза?
А) 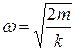 ;Б)
;Б) 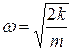 ;В)
;В) 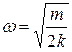 ; Г)
; Г) 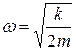 .
.
3 Две пружины жесткостью k каждая соединили последовательно и подвесили к ним груз массой m. Чему равна циклическая частота колебаний груза?
А) 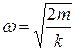 ; Б)
; Б) 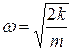 ;В)
;В) 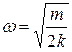 ; Г)
; Г) 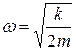 .
.
4 Груз массой m0 = 100 г, подвешенный на пружине, совершает гармонические колебания с периодом T0 = 4 с. К этому грузу подвесили еще
один груз массой m = 300 г. Определите период колебаний T' после подвешивания груза.
А) 16 с; Б) 12 с; В) 8 с; Г) 4 с.
5 На рисунке изображена зависимость координаты пружинного маятника от времени. Определите жесткость пружины маятника, если масса груза 4 кг.
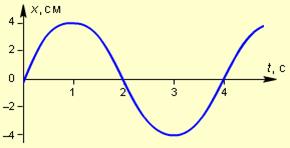
А) 0,1 Н/м; Б) 0,41 Н/м; В) 9,8 Н/м; Г) 19,6 Н/м.
6 Всегда ли математический маятник совершает гармонические колебания, будучи отклоненным от положения равновесия?
А) всегда, если только выполнены условия, позволяющие считать маятник математическим (масса груза много больше массы подвеса, длина подвеса много больше размеров груза);
Б) не всегда, только при малых углах отклонения от положения равновесия 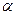 < 100;
< 100;
В) только при условии нахождения маятника в инерциальной системе отсчета;
Г) груз на подвесе в любом случае совершает гармонические колебания.
7 Как изменится период колебаний математического маятника, если его длина увеличится в 9 раз?
А) Увеличится в 3 раза; Б) Уменьшится в 3 раза;
В) Увеличится в 9 раз; Г) Уменьшится в 9 раз.
8 Чему будет равен период малых колебаний математического маятника, если его удалить от поверхности Земли на расстояние, равное трем земным радиусам? Период колебаний маятника на поверхности Земли равен 1 с.
А) 1,7 с; Б) 3 с; В) 4 с; Г) 16 с.
9 Шар массой m, подвешенный на тонкой нити длиной l, совершает колебания с периодом 1 с. Каким будет период колебаний шара с массой 4m на нити длиной 4l?
А) 1 с; Б) 2 с; В) 4 с; Г) 16 с.
10 Пружинный маятник совершает гармонические колебания с амплитудой 20 см. Как изменится период колебаний этого маятника при уменьшении амплитуды колебаний до 10 см?
А) Увеличится в 2 раза; Б) Уменьшится в 2 раза;
В) Уменьшится в 1,41 раза; Г) Не изменится.
11 Как изменится период колебаний математического маятника, если амплитуду его колебаний уменьшить в 2 раза? Сопротивление воздуха отсутствует.
А) Уменьшится в 2 раза ; Б) Уменьшится в 1,41 раза;
В) Не изменится; Г) Ответ зависит от длины подвеса маятника.
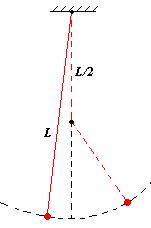 12 Математический маятник длины L совершает колебания. На пути маятника вбили гвоздь так, как показано на рисунке. Каким стал период колебания маятника?
12 Математический маятник длины L совершает колебания. На пути маятника вбили гвоздь так, как показано на рисунке. Каким стал период колебания маятника?
А) 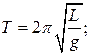 Б)
Б) 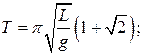
В) 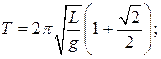 Г)
Г) 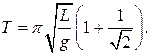
13 Тяжелый однородный стержень колеблется, будучи закрепленным шарнирно за один из концов. Как изменится период колебаний стержня, если ость вращения будет проходить через его середину?
А) Увеличится в 2 раза; Б) Увеличится в 1, 41 раза;
В) Не изменится; Г) Маятник перестанет колебаться.
14 Тяжелый однородный стержень колеблется, будучи закрепленным шарнирно за один из концов. Как изменится период колебаний, если плотность материала, из которого изготовлен стержень, увеличить в 2 раза?
А) Уменьшится в 2 раза; Б) Уменьшится в 1,41 раза;
В) Не изменится; Г) Увеличится в 1,41 раза.
15 Тяжелый однородный стержень длиной L колеблется, будучи закрепленным шарнирно за один из концов. Какую длину должен иметь математический маятник, чтобы период его колебаний был равен периоду колебаний стержня?
А) L; Б) L/2; В) 2L/3; Г) 3L/2.
16 Как изменится частота колебаний физического маятника, если точку подвеса перенести в центр качания (точку, находящуюся ниже точки подвеса на расстоянии, равном приведенной длине маятника)?
А) Маятник перестанет колебаться; Б) Частота колебаний увеличится;
В) Частота колебаний уменьшится; Г) Частота колебаний не изменится.
Тест № 3 «Динамика гармонических колебаний»
1 При гармонических колебаниях пружинного маятника с периодом 1 с и амплитудой 12 см тело достигло максимальной скорости. Чему равно в этот момент смещение тела относительно положения равновесия?
А) 0 см; Б) 12 см; В) – 12 см.
Г) Ответ дать не возможно, так как неизвестно, каким образом тело привели в колебательное движение.
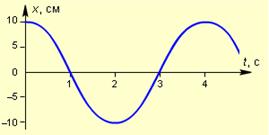 2 На рисунке показана зависимость координаты колеблющегося тела от времени. Чему равна скорость тела через 1 с после начала колебаний?
2 На рисунке показана зависимость координаты колеблющегося тела от времени. Чему равна скорость тела через 1 с после начала колебаний?
А) 0, 25 см/с; Б) 1,57 см/c; В) 6,4 см/с; Г) 15,7 см/c.
3 На рисунке показана зависимость координаты колеблющегося тела от времени. Чему равен модуль ускорение тела через 2 с после начала колебаний?
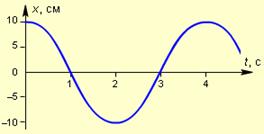
А) 0,41 см/с2; Б) 2,46 см/с2; В) 4,06 см/с2; Г) 24,65 см/с2.
4 Материальная точка совершает гармонические колебания. В какой из моментов – 1, 2 или 3 достигаются максимальные значения: А) кинетической энергии; В) потенциальной энергии; С) ускорения (по модулю).
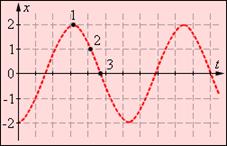
А A) 3, В) 1, С) 2; Б A) 2, В) 1, С) 3;
В A) 1, В) 3, С) 2; Г A) 3, В) 1, С) 1.
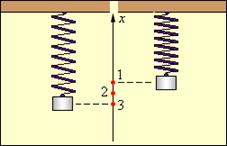
5 Груз, подвешенный на пружине, совершает свободные колебания между точками 1 и 3. В каких точках равнодействующая всех сил, приложенных к грузу, максимальна по модулю?
А) Только в точке 1; Б) Только в точке 2;
В) Только в точке 3; Г) В точках 1 и 3.
6 Груз массой 0,1 кг прикрепили к пружине школьного динамометра жесткостью 40 Н/м. В начальный момент времени пружина не деформирована. После того, как груз отпускают, возникают колебания. Чему равна максимальная скорость груза?
А) 0,25 м/с; Б) 0,5 м/с; В) 1 м/с; Г) 2 м/с.
7 Максимальное значение потенциальной энергии свободно колеблющегося маятника 8 Дж, а максимальное значение его кинетической энергии 8 Дж. В каких пределах изменяется его полная механическая энергия? Трением в системе пренебречь.
А) Не изменяется и равна 8 Дж;
Б) Не изменяется и равна 16 Дж;
В) Изменяется в пределах от 0 до 8 Дж;
Г) Изменяется в пределах от 0 до 16 Дж.
8 Тело, подвешенное на пружине, совершает гармонические колебания с частотой ν. С какой частотой происходит изменение полной механической энергии тела? Трением в системе пренебречь.
А) ν; Б) ν/2; В) 2 ν;
Г) Полная механическая энергия не изменяется.
Тест № 4 «Дифференциальное уравнение гармонических колебаний»
1 Для доказательства того, что в системе происходят гармонические колебания, необходимо получить дифференциальное уравнение вида:
А) 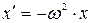 ; Б)
; Б) 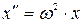 ;
;
В) 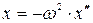 ; Г)
; Г) 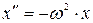 .
.
где 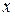 - координата тела, являющаяся функцией от времени
- координата тела, являющаяся функцией от времени 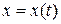
2 Составьте правильное утверждение
Для нахождения циклической частоты гармонических колебаний, совершаемых какой-либо системой, необходимо…
А) воспользоваться справочником или учебником;
Б) построить аналогию с пружинным маятником и заменить жесткость пружины и массу груза в выражении 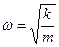 на соответствующие величины, характеризующие рассматриваемую колебательную систему;
на соответствующие величины, характеризующие рассматриваемую колебательную систему;
В) получить для рассматриваемой колебательной системы дифференциальное уравнение вида 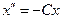 , где С – положительная константа. Циклическая частота колебаний равна
, где С – положительная константа. Циклическая частота колебаний равна 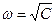 ;
;
Г) получить для рассматриваемой колебательной системы дифференциальное уравнение вида 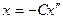 , где С – положительная константа. Циклическая частота колебаний равна
, где С – положительная константа. Циклическая частота колебаний равна 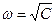 .
.
3 Составьте правильное утверждение
Для нахождения периода гармонических колебаний, совершаемых какой-либо системой, необходимо…
А) воспользоваться справочником или учебником;
Б) построить аналогию с пружинным маятником и заменить жесткость пружины и массу груза в выражении 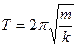 на соответствующие величины, характеризующие рассматриваемую колебательную систему;
на соответствующие величины, характеризующие рассматриваемую колебательную систему;
В) получить для рассматриваемой колебательной системы дифференциальное уравнение вида 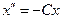 , где С – положительная константа. Из уравнения находим циклическую частоту колебаний
, где С – положительная константа. Из уравнения находим циклическую частоту колебаний 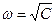 и период колебаний
и период колебаний 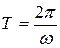 ;
;
Г) получить для рассматриваемой колебательной системы дифференциальное уравнение вида 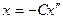 , где С – положительная константа. Из уравнения находим циклическую частоту колебаний
, где С – положительная константа. Из уравнения находим циклическую частоту колебаний 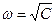 и период колебаний
и период колебаний 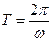 .
.
4 Составьте правильное утверждение
Период свободных (или собственных) гармонических колебаний, совершаемых колебательной системой, зависит от…
А) способа выведения системы из положения равновесия;
Б) энергии, сообщенной системе при выведении ее из положения равновесия;
В) параметров самой колебательной системы;
Г) энергии, сообщенной системе при выведении ее из положения равновесия, и параметров самой колебательной системы.
5 При решении задачи отличник Женя Петров получил уравнение 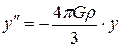 , где у – это координата тела. Какова циклическая частота гармонических колебаний, совершаемых телом?
, где у – это координата тела. Какова циклическая частота гармонических колебаний, совершаемых телом?
А) полученное уравнение не является дифференциальным уравнением гармонических колебаний;
Б) 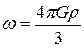 ; В)
; В) 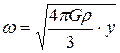 ; Г)
; Г) 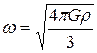 .
.
6 При решении задачи получено дифференциальное уравнение 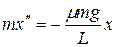 , где х – координата тела. Как выглядит уравнение движения этого тела?
, где х – координата тела. Как выглядит уравнение движения этого тела?
А) 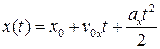 ; Б)
; Б) 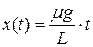 ;
;
В) 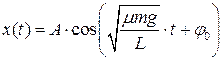 ; Г)
; Г) 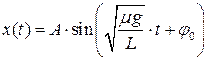 .
.
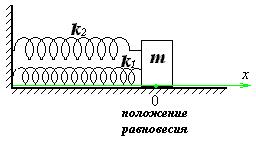 7 Колебательная система состоит из груза массы m и двух пружин жесткостями k1 и k2. В положении равновесия первая пружина растянута, вторая сжата. Какое дифференциальное уравнение описывает колебания системы? Поверхность стола гладкая.
7 Колебательная система состоит из груза массы m и двух пружин жесткостями k1 и k2. В положении равновесия первая пружина растянута, вторая сжата. Какое дифференциальное уравнение описывает колебания системы? Поверхность стола гладкая.
А) 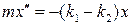 ; Б)
; Б) 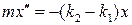 ;
;
В) 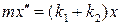 ; Г)
; Г) 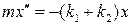 .
.
Динамика колебательного движения
 |
1 На горизонтальной пружине укреплено тело массы М = 10 кг, лежащее на абсолютно гладком столе. В это тело попадает и застревает в нем пуля массы m = 10 г, летящая со скоростью v = 500 м/с, направленной вдоль оси пружины. Амплитуда возникших при этом колебаний А = 0,1 м. Определите период возникших колебаний Т.
2 К одному концу первоначально недеформированной и неподвижной пружины жесткости k прикреплен груз массы m. Свободный конец пружины стали тянуть с постоянной скоростью, как показано на рисунке, пока он не переместился на расстояние d. Затем его резко остановили. При какой скорости этого конца пружины груз после остановки не будет колебаться?
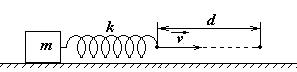 |
3 Чашка пружинных весов массы m совершает гармонические колебания с амплитудой А. В некоторый момент времени на нее положили (без начальной скорости) груз массой М. В результате колебания прекратились. Определите первоначальный период колебаний Т.
4 Точку подвеса математического маятника длины L мгновенно приводят в движение в горизонтальном направлении с постоянной скоростью v, затем, после того, как она переместилась на расстояние S, мгновенно останавливают. При каком значении скорости v колебания маятника, возникшие с началом движения, прекратятся сразу же после остановки? Перед началом движения маятник покоился. Колебания маятника считать малыми.
5 Горизонтальная подставка совершает в вертикальном направлении гармонические колебания с амплитудой А. Какой должна быть циклическая частота w этих колебаний, чтобы лежащий на подставке предмет не отделялся от нее?
6 Одна из обкладок незаряженного плоского конденсатора площади S подвешена на пружине, вторая обкладка закреплена неподвижно. Расстояние между пластинами в начальный момент равно L0. Конденсатор на короткое время подключили к батарее, и он зарядился до напряжения U. Какой должна быть жесткость пружины k, чтобы не произошло качания пластин в результате их взаимного притяжения после зарядки?
Составление дифференциального уравнения гармонических колебаний и нахождение периода малых колебаний
1 Используем второй закон динамики Ньютона (для поступательного движения).
Помним, что при решении координата груза (отсчитываемая, кстати, от положения равновесия) не всегда равна удлинению пружины!!
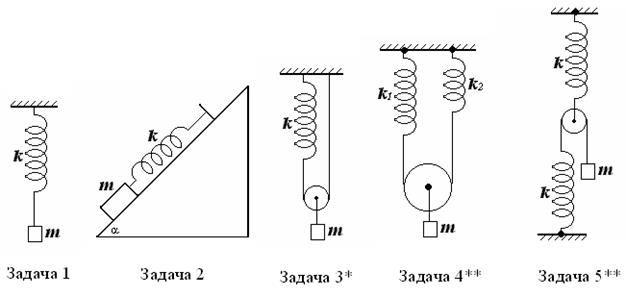
Указания к решению задач
Задача 1 - очень просто! Не забудьте, что в процессе движения на груз действует не только пружина. В положении равновесия пружина деформирована, значит, координата груза и величина деформации пружины численно не совпадают.
Задача 2 - после первой задачи разобраться в этой ситуации не сложно. Действуем так же.
Задача 3 – (МФТИ) -казалось бы, что изменилось в сравнении с первой ситуацией! Пружина и нерастяжимый трос по-прежнему невесомы. Просто добавился невесомый блок. Физика существенно изменилась!
Вспомните не только кинематические, но и динамические связи!
Задача 4 – (МГУ) – пружин стало две, а нить по-прежнему невесома. Подумайте, как соединены между собой пружины, каковы силы упругости, возникшие в них. Ну и, конечно, не забудьте кинематические и динамические связи.
Задача 5 - эта задача предлагалась на окружной олимпиаде. Конечно, не просто не забыть обо всем…
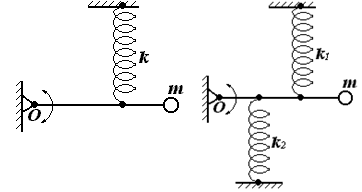 | 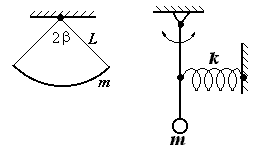 | ||
2 Используем второй закон динамики вращательного движения
