Апериодическое звено 2-го порядка

(Слайд 13)

Звено относится к группе позиционных звеньев и описывается уравнением

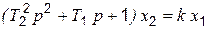. (4.14)

При этом корни характеристического уравнения

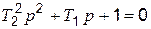(4.15)

должны быть вещественными, что будет выполняться при условии Т₁ ≥ 2 Т₂ .

Левая часть уравнения (4.14) разлагается на множители

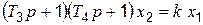, (4.16)

(Слайд 14)

где

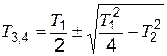. (4.17)

Передаточная функция звена

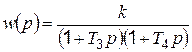. (4.18)

Из последнего выражения видно, что апериодическое звено второго порядка эквивалентно двум апериодическим звеньям первого порядка, включенным последовательно друг за другом, с общим коэффициентом передачи k и постоянными времени Т₃ и Т₄.

(Слайд 15)

Примеры апериодических звеньев второго порядка приведены на рис. 4.7, где а – две последовательно соединенные RL-цепи, б – две RС-цепи, в – двигатель постоянного тока.

Рис. 4.7. Апериодические звенья второго порядка

(Слайд 16)

Переходная функция получается путем решения дифференциального уравнения (4.14) при x₁ = 1(t) и нулевых начальных условиях, то есть при t = 0; x₂ = 0 и .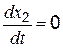

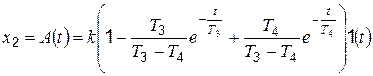. (4.19)

Функция веса

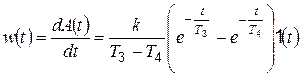. (4.20)

(Слайд 17)

Временные характеристики звена изображены на рис. 4.8 (для определенности принято T₃ > T₄).

На переходной характеристике показано построение, позволяющее по экспериментальным данным определять постоянные времени Т₃ и Т₄.

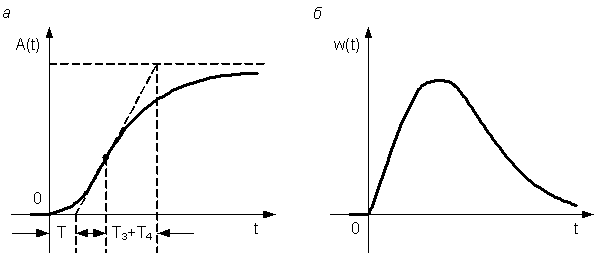
Рис. 4.8 Переходная функция (а) и дельта-функция (б)
апериодического звена второго порядка

(Слайд 18)

Частотная передаточная функция согласно (4.18), её модуль и фаза соответственно равны

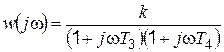; (4.21)

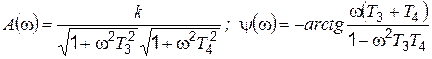. (4.22)

(Слайд 19)

Амплитудная, фазовая и амплитудно-фазовая характеристики показаны на рис. 4.9. На амплитудно-фазовой характеристике отмечены три характерные точки: w = 0; .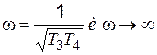

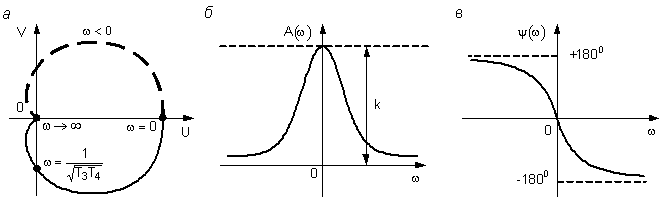
Рис. 4.9. АФЧХ (а), АЧХ (б) и ФЧХ (в) апериодического звена второго порядка

Построим теперь логарифмические характеристики (рис. 4.10). Для этой цели проведем вертикальные пунктирные прямые при сопрягающих частотах w₃ = 1 / T₃ и w₄ = 1 / T₄. Будем считать, что T₃ > T₄ и w₃ < w₄.

ЛАХ определяется выражением

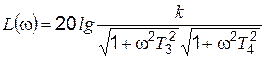. (4.23)

(Слайд 20)

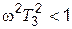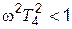Для частот, меньших, чем сопрягающая частота w₃ (а значит и меньших, чем частота ω₄), будет справедливым и . Поэтому в этой области можно допустить L(w) » 20 lgk. Этому выражению соответствует прямая а–b на рис. 4.10.

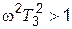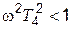Для частот w₃< w< w₄ будет справедливым и . Поэтому в этой области можно принять L(w) » 20 lg(k / wT₃), чему соответствует прямая с отрицательным наклоном 20 дБ/дек (прямая b-с на рис. 4.10).

Для частот 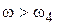имеем соответственно 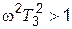и 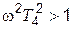, а также L(w) » 20 lg(k / wT₃T₄), чему соответствует прямая с отрицательным наклоном 40 дБ/дек (прямая с–d на рис. 4.10)

Ломаная линия а–b–с–d представляет собой асимптотическую ЛАХ. Действительная ЛАХ показана пунктиром. Она будет расходиться с асимптотической ЛАХ в местах изломов на 3 дБ.

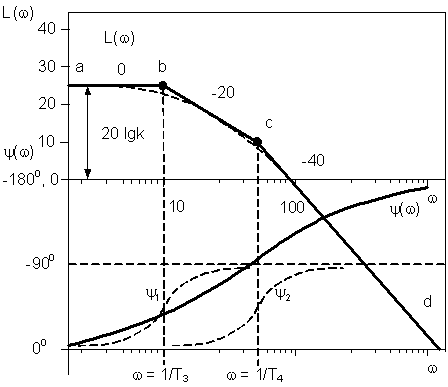
Рис. 4.10. ЛАХ и ЛФХ апериодического звена второго порядка

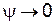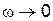ЛФХ получается суммированием двух слагаемых (см. второе уравнение (4.22)). Каждое слагаемое дает фазовую характеристику, совпадающую с ЛФХ апериодического звена первого порядка (рис. 4.10). В результате суммирования получаем ЛФХ, ордината которой соответствует при и 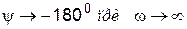.