Тема 5. Кинетическая энергия и работа вращательного движения Уравнение динамики вращательного движения твердого тела
При вращении твердого тела относительно неподвижной оси отдельные его точки, находящиеся на различном расстоянии от оси вращения, имеют различные скорости 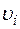 . Поэтому для того, чтобы найти кинетическую энергию вращательного движения твердого тела,необходимо разбить это тело на элементарные объемы так, чтобы каждый элементарный объем можно было рассматривать как материальную точку массой
. Поэтому для того, чтобы найти кинетическую энергию вращательного движения твердого тела,необходимо разбить это тело на элементарные объемы так, чтобы каждый элементарный объем можно было рассматривать как материальную точку массой 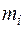 , находящуюся на определённом расстоянии
, находящуюся на определённом расстоянии 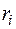 от данной оси вращения. Тогда кинетическая энергия вращательного движения твердого тела
от данной оси вращения. Тогда кинетическая энергия вращательного движения твердого тела 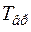 равна суммекинетических энергий всех n материальных точек массами
равна суммекинетических энергий всех n материальных точек массами 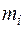 , на которые разбито это тело:
, на которые разбито это тело: 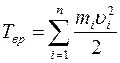 .
.
Так как для твердого тела угловая скорость вращения 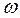 всех материальных точек, на которые разбито это тело, одинакова, то
всех материальных точек, на которые разбито это тело, одинакова, то
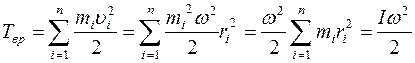 ,
,
где 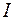 — момент инерции тела относительно его осивращения.
— момент инерции тела относительно его осивращения.
Момент силы.Если на тело, имеющее ось вращения ОО′,действует сила 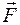 , причем вектор силы
, причем вектор силы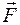 расположен в плоскости,перпендикулярной осиОО′ (рис. 5), то моментом этой силы
расположен в плоскости,перпендикулярной осиОО′ (рис. 5), то моментом этой силы 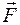 относительно неподвижной оси ОО′называется величина, равная произведению модуля силы
относительно неподвижной оси ОО′называется величина, равная произведению модуля силы 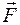 на плечо l этой силы относительно оси ОО′:
на плечо l этой силы относительно оси ОО′: 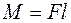 ,
,
где l – плечо силы 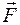 ,то есть кратчайшее расстояние между осью ОО′илинией действия силы
,то есть кратчайшее расстояние между осью ОО′илинией действия силы 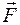 .
.
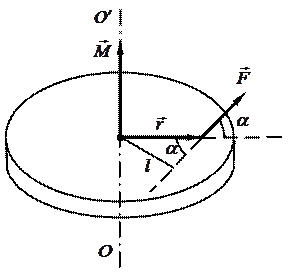
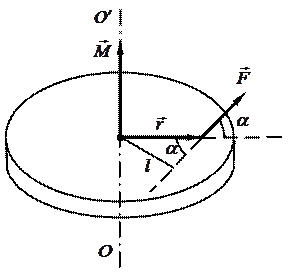 (Момент
(Момент 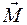 силы
силы 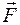 относительно оси вращения ОО′ является векторной величиной, определяется векторным произведением векторов
относительно оси вращения ОО′ является векторной величиной, определяется векторным произведением векторов 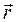 и
и 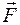 (рис. 5):
(рис. 5):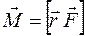 , направлен вдоль оси вращения ОО′ в соответствии с правилом правого винта, а модуль вектора
, направлен вдоль оси вращения ОО′ в соответствии с правилом правого винта, а модуль вектора 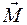 определяется в виде
определяется в виде 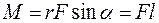 ).
).
Рис. 5
Работа при вращении твердого тела. При повороте тела на бесконечно малый угол 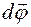 вокруг оси OO′ под действием силы
вокруг оси OO′ под действием силы 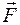 совершается элементарная работа:
совершается элементарная работа: 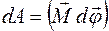 ,
,
где 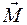 – момент силы
– момент силы 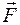 относительно оси OO′.
относительно оси OO′.
Уравнение динамики вращательного движения твердого тела. Уравнение динамики вращательного движения твердого тела может быть получено, исходя из того, что элементарная работа при вращении твердого тела идет на элементарное увеличение его кинетической энергии, то есть:
dA=dT.
Так как 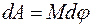 , а
, а 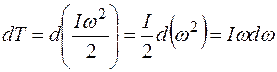 , то
, то
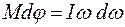 или
или 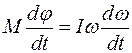 .
.
Учитывая, что 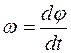 , а
, а 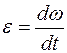 ,
,
получим: 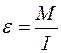
или в векторном виде: 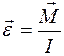 .
.
В приведенной формуле: 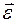 – вектор углового ускорения;
– вектор углового ускорения;
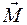 – вектор момента силы, действующей на тело, относительно его оси вращения; I – момент инерции тела относительно его оси вращения.
– вектор момента силы, действующей на тело, относительно его оси вращения; I – момент инерции тела относительно его оси вращения.
В том случае, если на тело, имеющее ось вращения, действует не одна, а несколько сил, то приведенный в этой формуле момент силы 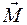 является результирующим моментом всех действующих на это тело сил и определяется векторной суммой всех моментов действующих сил относительно оси вращения данного тела.
является результирующим моментом всех действующих на это тело сил и определяется векторной суммой всех моментов действующих сил относительно оси вращения данного тела.
Это уравнение естьуравнение динамики вращательного движения твердого тела: если на тело, имеющее ось вращения, действуют силы, то это тело приобретает угловое ускорение, прямо пропорциональное векторной сумме моментов всех действующих сил и обратно пропорциональное моменту инерции тела относительно его оси вращения.
