Нахождение корней уравнения
УДК 681.3
Информатика. Основы программирования. Индивидуальные задания./ Методические указания. /Сост. ст. преп. Нартова М.М., ст. преп. Осипова П.М., ст. преп. Усова Э.А. – Новосибирск: Изд-во СГУПСа, 2004. - 45 с.
Содержат варианты заданий для лабораторных работ, используемых при выполнении лабораторных работ по курсу “Информатика”. Предназначены для студентов всех специальностей.
Рассмотрены и рекомендованы к печати на заседании кафедр «Общая информатика» и «Информационные технологии транспорта».
Ответственный редактор
канд. техн. наук, доцент Косенюк В.К.
Рецензент
Сибирский государственный университет путей сообщения, 2004
Лабораторная работа 1
Линейная программа
Цель работы – изучение основных понятий и принципов организации линейных вычислительных процессов и овладение практическими навыками составления программ.
Программа, операторы которой выполняются последовательно, в естественном порядке, называется линейной. По линейным программам выполняются расчёты по формулам.
Прежде чем составлять программу, необходимо выполнить следующее:
установить порядок вычислений по формулам;
выполнить классификацию данных (исходные, промежуточные, окончательные);
присвоить имена переменным в соответствии с правилами языка.
Задания
1.Вычислить: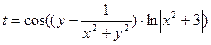 
, х = p, y – задать вводом.
2.Вычислить: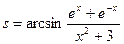 
, х- задать вводом.
3.Вычислить:
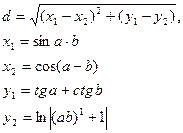
a и b – задать вводом.
4.Вычислить: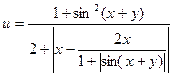 
, х и у – задать вводом.
5.Вычислить:
,
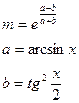х – задать вводом.
6.Вычислить:
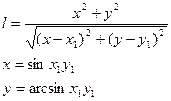
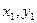- задать вводом.
7.Вычислить:
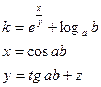
где a=5, b=10. Z – задать вводом.
8.Вычислить:
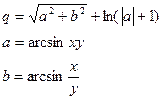
х и у – задать вводом.
9.Вычислить:
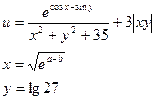
a и b – задать вводом.
10.Вычислить:
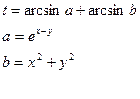
х и у – задать вводом.
11.Вычислить:
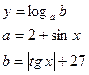
х – задать вводом.
12.Вычислить:
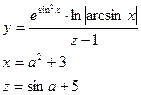
а – задать вводом.
13.Вычислить:
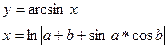
a и b– задать вводом.
14.Вычислить: 
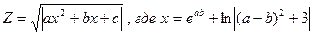, a,b,c– задать вводом.
15.Вычислить:
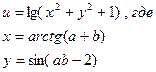
a и b– задать вводом.
16.
Вычислить:
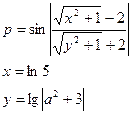
а – задать вводом.
17.Вычислить: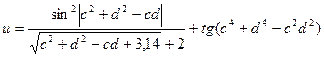 
, c, d– задать вводом.
18.Вычислить:
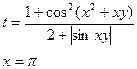
у – задать вводом.
19.Вычислить:
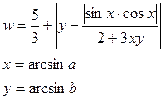
a и b– задать вводом.
20.Вычислить:
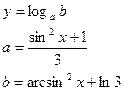
х– задать вводом.
21.Вычислить:
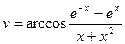
х – задать вводом.
22.Вычислить: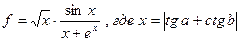 
, a и b– задать вводом.
23.Вычислить: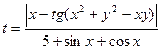 
, х и у – задать вводом.
24.Вычислить:
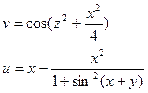
x, y, z – задать вводом.
25.Вычислить:
,
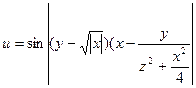x, y, z– задать вводом.
26.Вычислить:
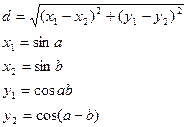
a и b– задать вводом.
27.Вычислить:
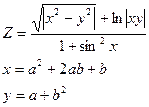
a и b– задать вводом.
28.Вычислить:
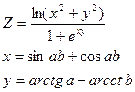
a и b– задать вводом.
29.Вычислить:
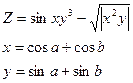
a и b– задать вводом.
30.Вычислить:
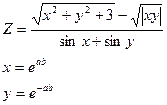
a и b – задать вводом.
Лабораторная работа 2
Простой цикл
Цель работы – изучение основных принципов организации циклов с явным числом повторений и получение навыков составления и отладки программ.
Понятие циклического вычислительного процесса. Часто при решении задач на ЭВМ требуется многократно выполнять какую-либо совокупность действий при различных исходных данных - вычисление функций при изменяющихся значениях аргумента, получение сумм нескольких слагаемых и т.д. Алгоритмы, реализующие такие расчёты, называются циклическими.
В циклических алгоритмах в отличие от линейных происходит нарушение естественного порядка выполнения расчётов.
Основными элементами циклического алгоритма являются тело цикла и его настройка. Телом цикла называется последовательность многократно выполняемых указаний. Настройка цикла – первоначальная подготовка переменных, значения которых должны быть определены к моменту работы цикла.
Для обеспечения правильности работы циклического алгоритма необходимо соблюдать следующее:
настройка цикла должна предшествовать телу и исполняться только один раз;
в теле цикла необходимо осуществлять обновление данных;
для обеспечения своевременного выхода из цикла (чтобы он не затягивался до бесконечности) нужно делать проверку условия повторения цикла. Это условие зависит от решаемой задачи.
Различают циклы с явным числом повторений и неявным числом повторений.
Циклы с явным числом повторений. В таких циклах число повторений n заранее известно. Оно зависит от разных факторов: числа слагаемых при подсчёте суммы, количества значений аргумента при вычислении функции и др. В первом случае n задаётся в условии программируемой задачи, во втором также может быть задано заранее, либо определено (если аргумент изменяется закономерно) по формуле:
N = [(a-b)/h] +1,
где b, a- верхняя и нижняя границы изменения аргумента; h – шаг изменения аргумента. От выражения в скобках берётся целая часть.
В дальнейшем цикл с явным числом повторений будем называть простым, а переменную, контролирующую число его повторений, параметром цикла (управляющей переменной).
Задания
1. Вычислить: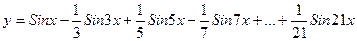 
. Значение Х задать вводом.
2. Вычислить: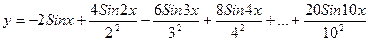 
. Значение Х задать вводом.
3. Вычислить: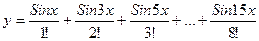 
. Значение Х задать вводом.
4. Вычислить: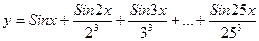 
. Значение Х задать вводом.
5. Вычислить: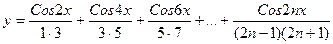 
, где n=20. Значение Х задать вводом.
6. Вычислить: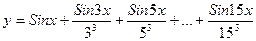 
. Значение Х задать вводом.
7. Вычислить: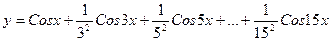 
. Значение Х задать вводом.
8. Вычислить: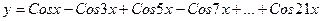 
. Значение Х задать вводом.
9. Вычислить: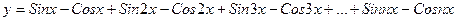 
, где n=25. Значение Х задать вводом.
10. Вычислить: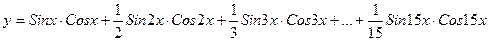 
. Значение Х задать вводом.
11. Вычислить: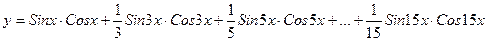 
. Значение Х задать вводом.
12. Вычислить: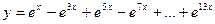 
. Значение Х задать вводом.
13. Вычислить: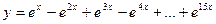 
. Значение Х задать вводом.
14. Вычислить: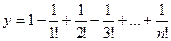 
. Значение n задать вводом.
15. Вычислить: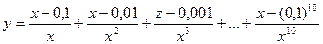 
. Значение Х задать вводом.
16. Вычислить: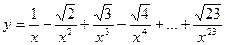 
. Значение Х задать вводом.
17. Вычислить: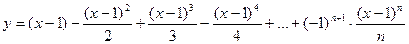 
, где n=30.Значение Х задать вводом.
18. Вычислить: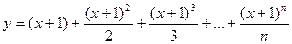 
, где n=25. Значение Х задать вводом.
19. Вычислить: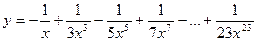 
. Значение Х задать вводом.
20. Вычислить: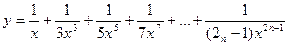 
, где n=20. Значение Х задать вводом.
21. Вычислить: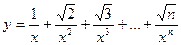 
, n=20. Значение Х задать вводом.
22. Вычислить: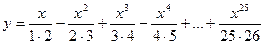 
. Значение Х задать вводом.
23. Вычислить: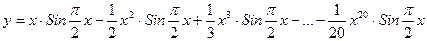 
. Значение Х задать вводом.
24. Вычислить: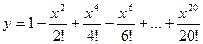 
.
25. Вычислить: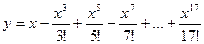 
. Значение Х задать вводом.
26. Вычислить: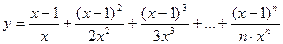 
, где n=25. Значение Х задать вводом.
27. Вычислить: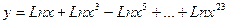 
. Значение Х задать вводом.
28. Вычислить: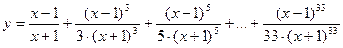 
. Значение Х задать вводом.
29. Вычислить: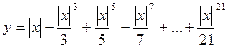 
. Значение Х задать вводом.
30. Вычислить: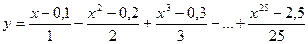 
. Значение Х задать вводом.
Лабораторная работа 3
Разветвления в программе
Цель работы – изучение основных принципов организации разветвлений и получение навыков составления и отладки программ.
Обычно шаги алгоритма выполняются в том порядке, в котором они перечислены. Однако во многих алгоритмах последовательность шагов зависит от значений исходных данных. В таких случаях в зависимости от значений некоторых переменных нужно выбрать ту или иную последовательность шагов.
Выбор нужной ветви алгоритма обычно производится по результату проверки некоторого условия. Шаг алгоритма, на котором выполняется проверка условия, называется шагом выбора или шагом ветвления. Простейший вид шага выбора представляет собой проверку логического условия, т.е. условия, которое может быть истинным или ложным.
Шаг выбора может быть с одной и двумя альтернативами.
Шаг выбора, при котором нужно выполнять одну последовательность действий, если условие истинно, и другую, если условие ложно, считается шагом выбора (ветвления) с двумя альтернативами.
Шаг выбора, при котором необходимо выполнить некоторую последовательность действий в случае истинности условия и не нужно ничего выполнять, когда условие ложно, является шагом ветвления с одной альтернативой.
В обоих случаях в результате проверки условия, будет выбран только один из путей. После этого выполнение алгоритма будет продолжено (выполняется его очередной блок).
Алгоритм, содержащий хотя бы один шаг ветвления, называется разветвляющимся.
Задания
1.Написать программу решения уравнения вида: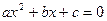 
2.Написать программу решения уравнения вида: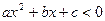 
3.Написать программу решения уравнения вида: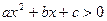 
4.Написать программу решения уравнения вида: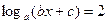 
5.Написать программу решения уравнения вида: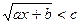 
. Проверить, является ли х – решением.
6.Написать программу решения уравнения вида: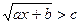 
. Проверить, является ли х – решением.
7. Написать программу решения уравнения вида: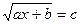 
8.Написать программу решения уравнения вида: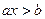 
9.
Написать программу решения неравенства вида: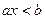 
10.
Написать программу поиска максимального значения из трёх чисел a,b,c, где
,
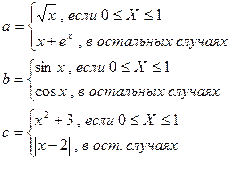Значение х задать вводом.
11.Написать программу поиска минимального значения из трёх чисел a,b,c, где
,
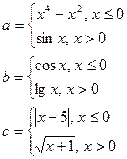значение х указать вводом.
12.Написать программу печати минимального элемента для a и b, где
,
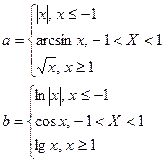значение х задать вводом.
13.Написать программу печати максимального элемента a и b, где
,
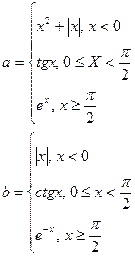значение х задать вводом.
14.Написать программу печати минимального значения среди трех элементов z,y,t, где:
,
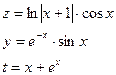значение х задать вводом.
15.Написать программу печати максимального значения среди z,y,t, где
,
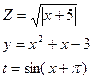значение х задать вводом.
16.Написать программу печати минимального значения среди z,y,t, где
,
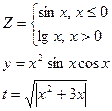значение х задать вводом.
17.Написать программу печати максимального значения среди z,y,t, где
,
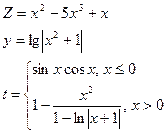значение х задать вводом.
18.Составить программу вычисления:
,
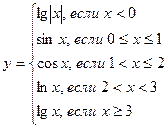значение х задать вводом.
19.Составить программу вычисления:
,
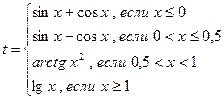где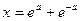 
.Значение а – задать вводом.
20.Составить программу вычисления:
,
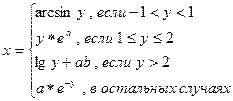значения а,b,у – задать вводом.
21.Написать программу вычисления пары функций z и y:
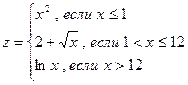
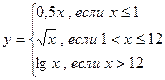
Значение х задать вводом.
22.Написать программу вычисления:
,
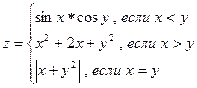где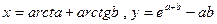 
. Значения a и b задать вводом.
23.Написать программу вычисления:
,
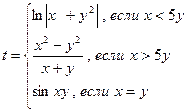где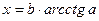 
, 
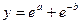, значения a и b задать вводом.
24.Составить программу вычисления:
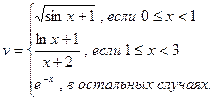
где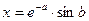 
, значения a и b задать вводом.
25.Составить программу вычисления:
,
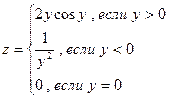где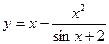 
, значения х задать вводом.
26.Составить программу вычисления:
,
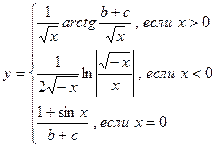значения b,c,х задать вводом.
27.Составить программу вычисления:
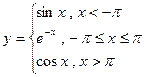
значенияаргумента х задать вводом.
28.Составить программу вычисления Z=2x-7, для которой:
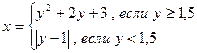
значение у задать вводом.
29.Написать программу для вывода сообщений о том, является ли х решением уравнения 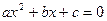. Значения a,b,c,x задать вводом.
30.Написать программу диагностики: является ли х решением неравенства: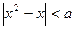 
. Значение х и а задать вводом.
Лабораторная работа 4
Циклы с разветвлением
Цель работы – получение навыков составления и отладки программ комбинированного типа.
На практике, алгоритмы, реализующие различные вычисления, представляют собой комбинацию основных базовых алгоритмов: линейного, циклического, разветвляющегося.
Задания
1. Для 10 произвольных значенийх подсчитать суммы:
1) всех чисел < 2;
2) всех чисел в интервале от –1 до 0;
3) остальных чисел.
2. Вычислить сумму тех значений функции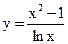 
, которые удовлетворяют условиюy > 13 .Аргумент х изменяется в интервале от 2 до 8 с шагом 0,5 .
3. Вычислить сумму положительных значений функции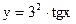 
для 19 значений х (произвольных). На печать выдать каждое вычисляемое значение и сумму положительных у.
4. Составить программу вычисления суммы положительных и суммы отрицательных значений функции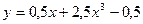 
для 
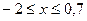с шагом 0,1
5. Составить программу вычисления количества положительных и отрицательных значений функции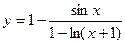 
при изменении аргумента x в интервале
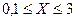с шагом 0,1. Нулевые значения функции не учитывать.
6. Составить программу вычисления и печати среднего арифметического положительных и среднего арифметического отрицательных значений функции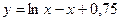 
. Аргумент х изменяется в интервале 
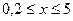c шагом h=0,25.
7. Составить программу вычисления суммы тех значений функции y , которые удовлетворяют условию: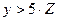 
, где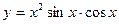 
, 
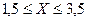Аргумент x изменяется с шагом 0,1.
8. Вычислить:
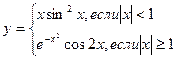
для 15 произвольных значений x. Подсчитать количество значений y, лежащих в интервале от 1 до 2.
9. Написать программу вычисления функции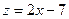 
, для которой
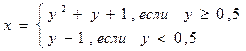
Значение y изменяется в интервале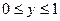 
с шагом h = 0,05.
10. Написать программу вычисления функций z и y
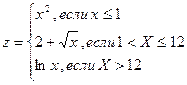
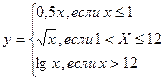
Аргумент изменяется в интервале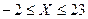 
c шагом h = 1.
11. Рассчитать и выдать на печать таблицу значений функции 
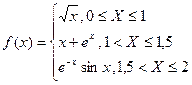
Шаг аргумента 0,1.
12. Составить программу вычисления суммы функции:
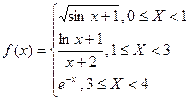
Шаг изменения аргумента h = 0,1.
13. Вычислить:
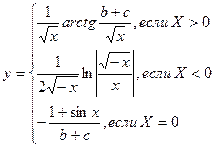
Значения b и c задать вводом.
14. Вычислить:
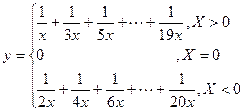
Для5различныхзначенийх.
15. Вычислить:
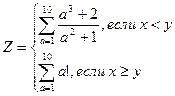
Значение X и Y задать вводом.
16. Вычислить:
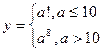
Параметр а изменяется в интервале от 1 до 12 с шагом 1.
17. Составить программу вычисления функций:
,
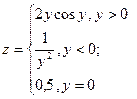где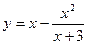 
для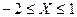 
с шагом 0,5. На печать вывести все значения x,y,z.
18. Составить программу вычисления функций:
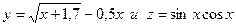при изменении аргумента x в интервале 
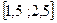с шагом h = 0,1.Найти суммы тех значений z, которые меньше 1; и сумму тех значений y которые 1<y<3.
19. Найти сумму тех членов последовательности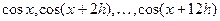 
, которые по абсолютной величине больше 0,5. x и y задать вводом.
20. Составить программу вычисления функции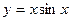 
при изменении аргумента в интервале 
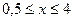c шагом h = 0,25. Печатать лишь те значения y, которые удовлетворяют условию 
.
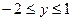21. Составить программу вычисления минимального значения функции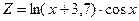 
при изменении аргумента x в интервале от 0до 6 с шагом 0,5.
22. Составить программу вычисления максимального значения функции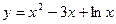 
при изменении аргумента х в интервале 
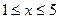c шагом 0,5.
23. Даны две функции
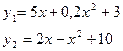
Определить координаты точек пересечения этих двух функций на участке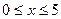 
с шагом 0,1. (Точка пересечения – min по модулю разность двух функций)
24. Определить и напечатать минимальную по модулю разницу между значениями двух функций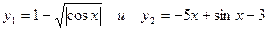 
, для которых аргумент изменяется в интервале от 0,5 до 6,5 с шагом 0,5. Напечатать так же то значение х, при котором эта разница достигается.
25. Ввести координаты m точек трехмерного пространства. Определить сколько из них лежит внутри сферы радиуса R с центром в начале координат.
26. Для 6 произвольных пар чисел (a,b) подсчитать и напечатать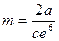 
где с- наибольшее по абсолютной величине из чисел a и b.
27. Для 15 произвольных значений x получить суммы тех чисел, которые:
1) кратны 5;
2) четные;
3) остальных чисел.
28. Для 5 произвольно введенных троек чисел (x,y,z) ответить на вопрос: « Можно ли образовать треугольник со сторонами x,y,z?»
29. Для 10 произвольно введенных чисел х подсчитать количество положительных и сумму отрицательных элементов.
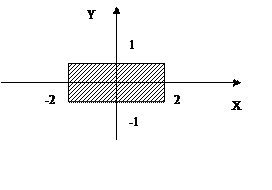
30. Для 10 произвольно введенных пар чисел (x , y) ответить на вопрос: «Принадлежит ли точка с координатами (x , y)области, изображенной на рисунке».
Лабораторная работа 5
Циклы с неявным числом повторений
Цель работы – изучение основных принципов организации циклов с неявным числом повторений и получение навыков составления и отладки программ.
В вычислительной практике часто встречаются циклы, число повторений которых заранее неизвестно, и выход из которых происходит при достижении определённого условия. Типичным примером является цикл, в основе которого лежит итерационный процесс, заключающийся в последовательном приближении искомой величины к своему конечному значению. Её начальное значение предварительно задаётся, а затем всякий раз уточняется через предыдущее значение. Выход из цикла происходит при достижении некоторой наперёд заданной точности. Эта точность может быть установлена по отношению к очередному приближённому значению искомой величины (очередному приближению), двум её соседним приближениям и т.д. Если при выполнении вычислений она достигается, то процесс считается сходящимся. Циклы, реализующие такие процессы, называются итерационными.
В практических вычислениях довольно часто приходится решать уравнения вида f(x) = 0. По методу простой итерации уравнение приводится к виду x = j(x). Начальное значение корня x0подставляется в правую часть этого уравнения, вычисляется новое приближение x1. Затем оценивается абсолютная величина разности между x1 иx0.Если она меньше заданной точности e, то любую из величин x1 иx0 можно считать корнем уравнения. В противном случае итерационный процесс продолжается, вычисляетсяx2 = j(x1) и так до тех пор, пока точность не будет достигнута. Отсюда видно, что полученное на очередном шаге вычислений (очередной итерации) приближённое значение корня является исходной величиной для следующего шага.
Задания
Нахождение корней уравнения
Метод простых итераций
Исходное нелинейное уравнение записываем в виде x = f(x). Подставляем начальное значение корня x = c0 в правую часть уравнения, получаем новое приближение с1 = f(c0) и т.д. Получаем сn+1 = f(cn), n=0,1,2, … Итерационный процесс прекращается, если результаты двух последних итераций близки, т.е. ½cn+1 - cn½ < e. Предусмотреть защиту от зацикливания.