Расчет переходного процесса в нелинейной цепи синусоидального тока.
5.1. Расчет нелинейной электрической цепи до коммутации в установившемся режиме методом дискретных резистивных схем с применением принципа расщепления.
Расчет будем проводить методом установления переходного процесса при нулевых начальных условиях.
Рассмотрим схему, представленную на рис. 29.
 |
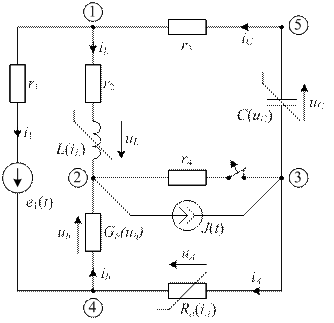| рис. 29 |
В данной схеме включены два нелинейных резистивных элемента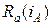 
и Gb(ub) и два нелинейных реактивных элемента L(iL) и C(iC), характеристики которых представлены в виде сплайнов (п.4.1)
Данной схеме будет соответствовать дискретная резистивная схема для момента времени tk (рис. 30) с начальными условиями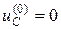 
, 
 |
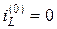
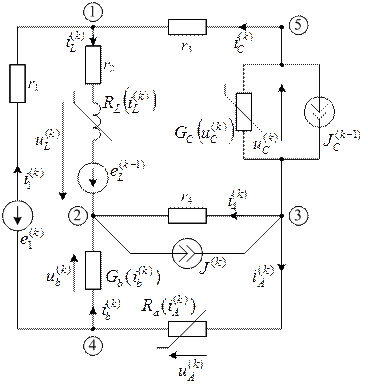| рис. 30 |
Уравнения гибридного типа для этой схемы имеют вид (индекс k для упрощения записей опущен)
В этих уравнениях
После расщепления система принимает вид:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
В матричной форме система имеет вид:
| iL | iC | ia | ib | i1 | i4 | φ1 | φ2 | φ3 | φ4 |
,
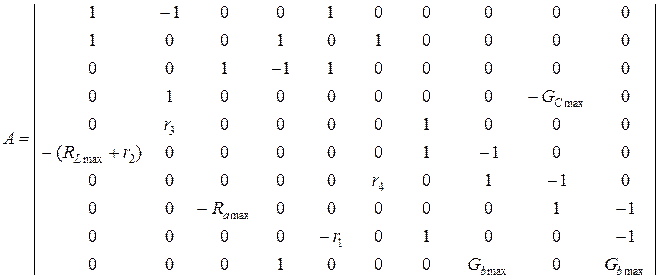| X01 | X02 | X03 | X04 | X05 | X06 | X07 | X08 | X09 | X010 |
, 
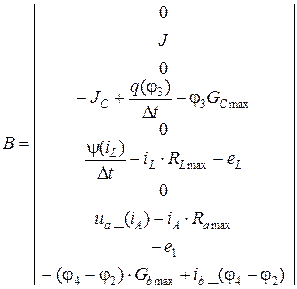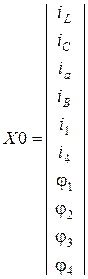
Дискретные значения источников в моменты времени вычисляются по формулам
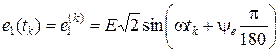
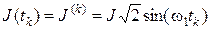
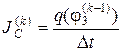
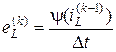
Значения E, ψe, J, ω1 берутся из исходных данных. В рассматриваемом примере , , ,
Результаты расчета в системе MathCAD приведены ниже
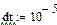
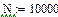
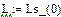
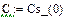
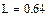
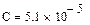
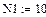
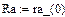
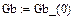
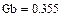
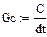
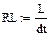
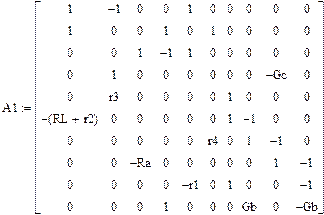
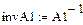
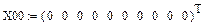
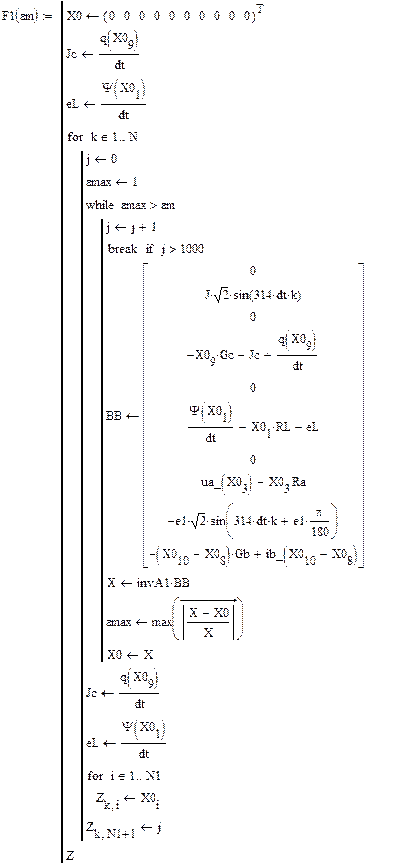
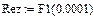
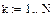
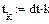
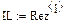
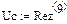
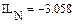
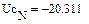
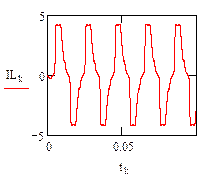
По результатам расчета можно определить ННУ: iL(–0) и uC(–0). Эти значения соответствуют установившимся мгновенным значениям iLуст(t) и uCуст(t) при . Для функции источника момент кратен периоду синусоидальных колебаний . В отрезке укладывается периодов синусоиды источника тока, т.е. при значение . Таким образом значению установившегося режима до коммутации соответствует момент коммутации схемы рис. 26, то есть в качестве ННУ для этой схемы при расчете переходного процесса после коммутации следует взять:
5.2. Расчет переходного процесса в цепи после коммутации методом дискретных резистивных схем
Схема после коммутации в дискретном представлении изображена на рис. 31
 |
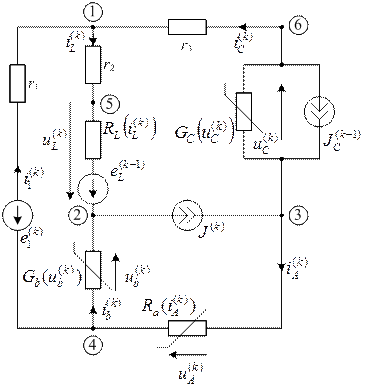| рис. 31 |
Система гибридных уравнений для схемы рис. 31 имеет вид: (). Индекс k для упрощения записей опущен.
, где
После расщепления уравнения примут вид:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
В матричной форме
| iL | iC | ia | ib | i1 | φ1 | φ2 | φ3 | φ4 | φ5 |
,
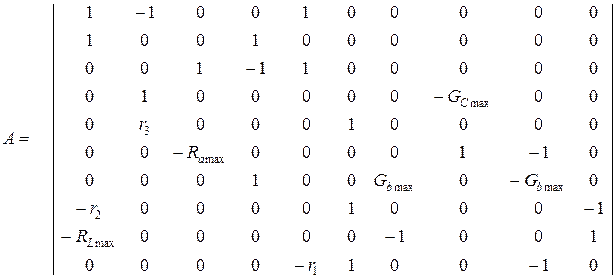| X01 | X02 | X03 | X04 | X05 | X06 | X07 | X08 | X09 | X010 |
, 
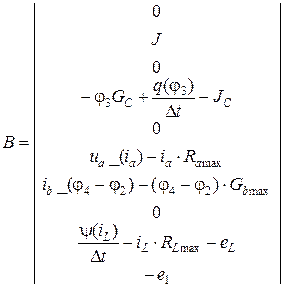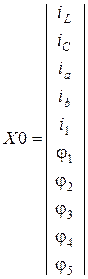
Дискретные значения источников в моменты времени вычисляются по формулам
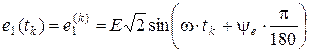
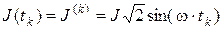
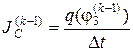
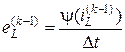, где q(uC) и ψ(iL) – сплайновые характеристики нелинейных реактивных элементов.
В качестве независимых начальных условий (ННУ) для расчета взяты рассчитанные в п.5.1. и . Зависимые начальные условия (ЗНУ) то есть значения можно рассчитать с помощью решающего блока GIVEN…FIND для уравнений Кирхгофа схемы после коммутации, записанных при
Такой расчет представлен ниже
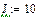
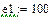
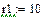
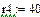
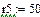
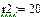
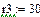
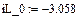
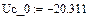
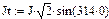
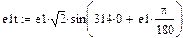
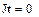
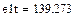
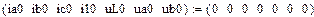
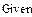
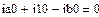
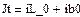
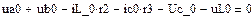
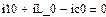
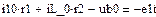
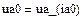
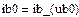
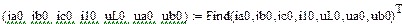
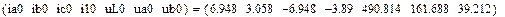
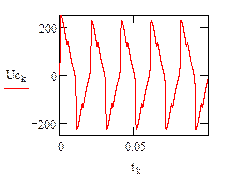
Результаты численного расчета переходного процесса в синусоидальном режиме приведены на рис. 32.
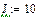
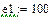
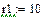
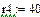
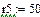
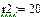
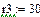
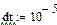
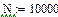
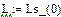
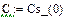
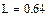
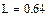
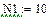
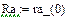
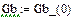
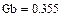
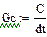
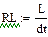
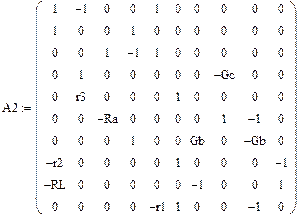
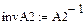
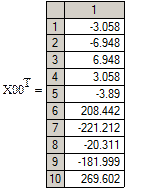
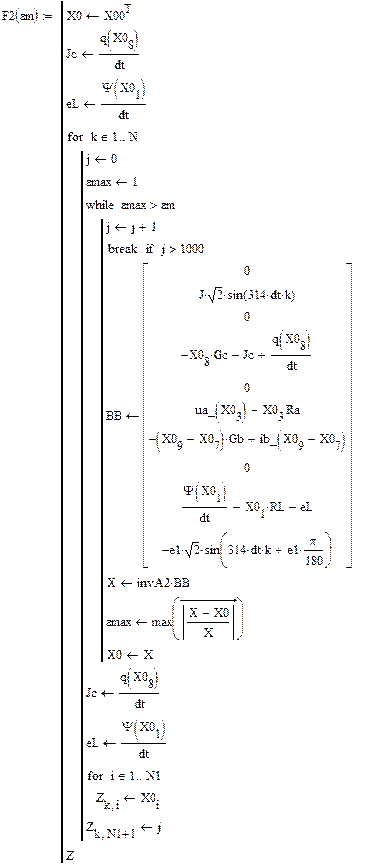
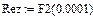
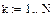
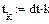
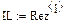
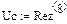
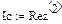
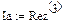
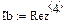
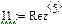
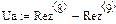
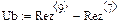
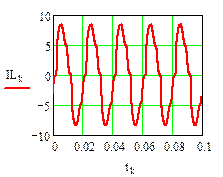
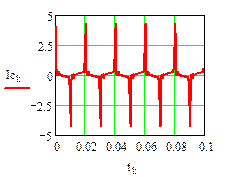
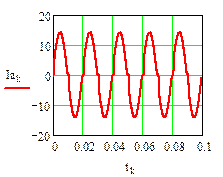
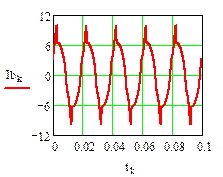
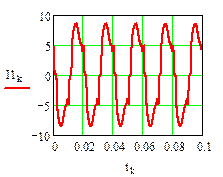
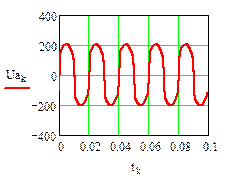
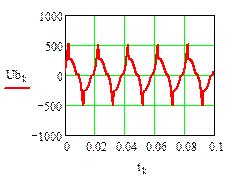
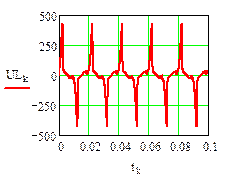
рис.32
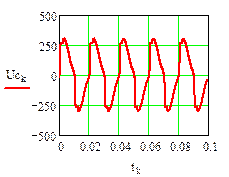
рис.32