Группоиды, полугруппы, группы

Тема1. ЭЛЕМЕНТЫ ОБЩЕЙ АЛГЕБРЫ

1. Основные алгебраические структуры.

2. Элементы теории множеств, операции и отношения над множествами.

3. Функции, отношения эквивалентности, отношения частичного порядка.

4. Группа Абелева, циклическая группа.

5. Изоморфизм, автоморфизм.

6. Кольцо, делители нуля. Тело, поле.

7.

8. Комплексные числа, действия над ними.

9. Тригонометрическая форма, сопряженные числа.

10. Формула Муавра.

Извлечение квадратного корня, корни высших степеней, корни из единицы, первообразные корни.

12. Многочлены одной переменной, операции над ними.

13. Алгоритм деления с остатком.

14. Делимость многочленов, ее свойства.

15. Наибольший общий делитель, алгоритм Евклида.

16. Метод Горнера.

17. Основная теорема алгебры (без док-ва). Формулы Виета.

Комплексные корни уравнения с действительными коэффициентами.

1.1

Алгебраическая система или алгебраическая структура — множество 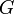(носитель) с заданным на нём набором операций (сигнатура), удовлетворяющим некоторой системе аксиом. То есть понятие алгебраической системы является специализацией понятия универсальной алгебры.

n-арная операция на G — это отображение прямого произведения n экземпляров множества в само множество 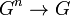. По определению, 0-арная операция — это просто выделенный элемент множества. Чаще всего рассматриваются унарные и бинарные операции, поскольку с ними легче работать. Но в связи с нуждами топологии, алгебры, комбинаторики постепенно накапливается техника работы с операциями большей арности, здесь в качестве примера можно привести теорию операд (клонов полилинейных операций) и алгебр над ними (мультиоператорных алгебр).

Для алгебраических систем естественным образом определяются морфизмы как отображения, сохраняющие операцию. Таким образом определяются категории групп, колец, R-модулей и т. п.

Если множество обладает структурой топологического пространства, и операции являются непрерывными, то называют топологической алгебраической системой. Так, в топологической группе операции умножения и взятия обратного элемента являются непрерывными.

Не все алгебраические конструкции описываются алгебраическими системами, в качестве примера иных можно упомянуть коалгебры, биалгебры, алгебры Хопфа и комодули над ними.

Список алгебраических систем

· Множество можно считать вырожденной алгебраической системой с пустым набором операций.

Группоиды, полугруппы, группы

· Группоид — множество с одной бинарной операцией 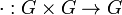, обычно называемойумножением.

· Правая квазигруппа — группоид, в котором возможно правое деление, то есть уравнение 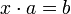имеет единственное решение для любых 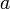и .

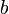· Квазигруппа — одновременно правая и левая квазигруппы.

· Лупа — квазигруппа с единичным элементом 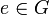, таким, что .

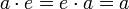· Полугруппа — группоид, в котором умножение ассоциативно: .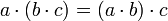

· Моноид — полугруппа с единичным элементом.

· Группа — моноид с делением. Для каждого элемента a группы можно определить обратный элемент a-1, такой, что .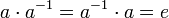

· Абелева группа — группа, в которой операция коммутативна, то есть, 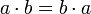. Операцию в абелевой группе часто называют сложением ('+').

Кольца

· Полукольцо — похоже на кольцо, но без обратимости сложения.

· Кольцо — структура с двумя бинарными операциями: абелева группа по сложению, моноид по умножению, выполняется закон дистрибутивности: .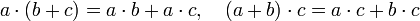

· Коммутативное кольцо — кольцо с коммутативным умножением.

· Целостное кольцо — кольцо, в котором произведение двух ненулевых элементов не равно нулю.

· Тело — кольцо, в котором ненулевые элементы образуют группу по умножению.

· Поле — коммутативное кольцо, являющееся телом.

Модули

· Модуль над кольцом 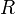— абелева группа по сложению, с дистрибутивной унарной операцией умножения на константу для каждого элемента кольца.

· Векторное пространство — модуль над полем.

Алгебры

Алгебра (линейная) — пространство с билинейной дистрибутивной операцией умножения, иначе говоря, кольцо с согласованной структурой пространства

· Ассоциативная алгебра — алгебра с ассоциативным умножением

· Алгебра термов

· Коммутативная алгебра

· Градуированная алгебра

· Алгебра Ли — алгебра с антикоммутативным умножением (обычно обозначаемым 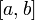), удовлетворяющим тождеству Якоби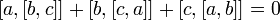

· Алгебра Йордана — коммутативная алгебра с тождеством слабой ассоциативности: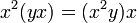

· Альтернативная алгебра — алгебра с тождествами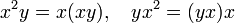

· Алгебра Мальцева — антикоммутативная алгебра с тождеством

·

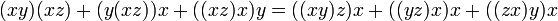
· Алгебра над операдой — один из наиболее общих видов алгебраических систем. Здесь сама операдаиграет роль сигнатуры алгебры.

Решётки

· Решётка — структура с двумя коммутативными, ассоциативными, идемпотентными операциями, удовлетворяющими закону поглощения.

· Булева алгебра.

1.2

Множества

Наиболее простая структура данных, используемая в математике, имеет место в случае, когда между отдельными изолированными данными отсутствуют какие-либо взаимосвязи. Совокупность таких данных представляет собой множество. Понятие множества является неопределяемым понятием. Множество не обладает внутренней структурой. Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством. Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия:

1. Должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности.
2. Должно существовать правило, позволяющее отличать элементы друг от друга. (Это, в частности, означает, что множество не может содержать двух одинаковых элементов).

Множества обычно обозначаются заглавными латинскими буквами. Если элемент 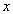принадлежит множеству 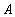, то это обозначается:

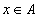
Если каждый элемент множества 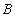является также и элементом множества 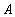, то говорят, что множество 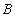является подмножеством множества :

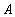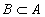
Подмножество 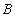множества 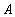называется собственным подмножеством, если

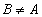
Используя понятие множества можно построить более сложные и содержательные объекты.