Метод отсечений гомори

В задачах целочисленного программирования в отличие от задач линейного программирования вводится дополнительное ограничение на переменные величины: они могут принимать лишь целые значения.

В некоторых задачах, например, транспортного типа, это условие выполняется автоматически, если исходные данные (количества отправляемых и получаемых грузов) выражены целыми числами. Но в общей задаче линейного программирования обычные методы решения целочисленности не гарантируют, независимо от того, целыми или дробными являются исходные величины.

В математической записи общая задача целочисленного программирования выглядит следующим образом:

максимизировать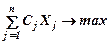

при условиях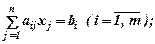

x_j ≥ 0, x_j – целые.

Экономические задачи линейного программирования чаще всего требует целочисленного решения. Это относится к задачам, в которых переменные величины обозначают количество единиц неделимой продукции, оборудования, работников (задачи наилучшего распределения производственных заданий между предприятиями, задачи оптимизации производственной программы отдельных предприятий, задачи оптимальной загрузки оборудования и др.). Часто такие задачи решаются обычным симплекс-методом с последующим округлением полученных значений переменных величин до целых чисел. Но в этом случае можно получить лишь некоторое приближение к действительно оптимальному целочисленному плану.

В другой группе задач линейного программирования подлежащими определению величинами являются производственные мощности, наиболее эффективно обеспечивающие заданную потребность. Поскольку «носителями» производственной мощности выступают отдельные предприятия, неделимые единицы оборудования и т. д., эти задачи также сводятся к целочисленным задачам линейного программирования.

Целочисленными являются также задачи рационального раскроя мерного материала (задачи на минимум отходов), так как переменные обозначают в них, как правило, количество исходных заготовок, раскраиваемое тем или иным способом.

Во всех упомянутых задачах решение может быть найдено обычными методами линейного программирования с последующей корректировкой и получением целочисленного плана, более или менее близкого к оптимальному. Но имеются задачи, нецелочисленное решение которых не имеет смысла. К ним относятся задачи выбора, в которых численные значения переменных служат лишь для определения альтернативы («или - или», «да – нет»).

К целочисленным моделям выбора относят некоторые задачи оперативно-календарного планирования, например, задачи об оптимальной последовательности запуска различных изделий (деталей) в производство. Допустим необходимо определить порядок запуска n деталей, каждая из которых последовательно обрабатывается на нескольких станках. Переменные х_ij равняются единице, если деталь j должна запускаться за деталью i, и нулю - во всех остальных случаях. Для каждого фиксированного j, так же как и для каждого i, только одна из n переменных может равняться единице, поэтому в число ограничений задачи входят следующие:

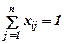и .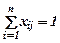

Минимизируется общее время обработки всех деталей на станках данной группы. Нецелочисленное решение такой задачи лишено смысла.

Существует несколько методов решения задач целочисленного программирования. Наиболее известен метод Гомори, основывающийся на использовании симплексного метода.

Рассмотрим математические понятия: конгруэнтности чисел, целой и дробной части числа. Число а конгруэнтно числу b в том и только том случае, когда разность а – b является целым числом. Конгруэнтность обозначают тремя горизонтальными черточками (≡); таким образом, а ≡ b, если а – b есть целое число.

Например: ⁵/₃ ≡ ²/₃, т.к. ⁵/₃ - ²/₃= 1;

-¹/₃ ≡ ²/₃, т.к.-¹/₃ - ²/₃= 1.

Все целые числа конгруэнтны друг другу и конгруэнтны нулю. Нецелочисленные элементы можно представить в виде суммы целой и дробной части числа а = [a] + {a}. Квадратные скобки означают взятие целой части числа, заключённого в них, фигурные – взятие дробной части числа.

Целой частью числа а называется наибольшее целое число [a], не превосходящее а.

Дробная часть числа а определяется как наименьшее неотрицательное число {a}, конгруэнтное числу а. Дробная часть числа а равна разности между числом а и его целой частью: {a}= а - [a]

Например, для а = 2¹/₃[a]= 2 {a} = ¹/₃

для a = - 2¹/₃[a]= -3 {a} = ²/₃

Свойства конгруэнтности чисел:

1. Если а ≡ b, то {а} = {b}.

2. {а+b} = {а} + {b}.

3. Если n - целое число, то для любого а

nа ≡ {nа} ≡ n{а}.

При решении задач целочисленного программирования методом Гомори первый этап совпадает с обычным расчетом по симплексному алгоритму. Полученное решение в общем виде будет удовлетворять всем условиям задачи, кроме требования целочисленности (не исключено, конечно, получение целочисленного решения уже на первом этапе). Если среди значений переменных в оптимальном плане (точка А на рис.13) есть дробные, то составляется дополнительное ограничение, как бы «отсекающее» дробную часть решения (линия 1 на рис.13), но оставляющее в силе все ограничения задачи, которым должен удовлетворять оптимальный план. Дополнительное ограничение присоединяется к исходным ограничениям задачи и к расширенной системе вновь применяется симплексная процедура. Если оптимальное решение снова окажется нецелочисленным (точка В на рис.13), то добавляется еще одно дополнительное ограничение (линия 2 на рис.13) и процесс вычислений повторяется. Алгоритм позволяет за конечное число шагов прийти к оптимальному целочисленному решению (если оно существует) (точка С на рис.13).

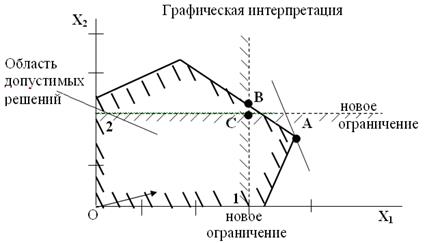
Рис. 13. Метод отсечений Гомори

Пример решения задачи целочисленного программирования. На приобретение оборудования для нового производственного участка выделено 20 ден.ед. Оборудование должно быть размещено на площади, не превышающей 38 м². Предприятие может заказать оборудование двух видов: более мощные машины типа А стоимостью 5 ден.ед, требующие производственную площадь 8 м² (с учетом проходов) и обеспечивающие производительность 7 тыс, единиц продукции за смену; менее мощные машины типа Б стоимостью 2 ден.ед, занимающие площадь 4 м² и дающие за смену 3 тыс, единиц продукции.

Требуется рассчитать оптимальный вариант приобретения оборудования, обеспечивающий при данных ограничениях максимум общей производительности участка.

Обозначим через х₁ количество приобретаемых машин А и через х₂ - количество приобретаемых машин Б, получаем математические условия задачи:

максимизировать 7х₁ + 3х₂ → max

при условиях: 5х₁ + 2х₂ ≤ 20

8х₁ + 4х₂ ≤ 38

х₁, х₂ ≥ 0 (целые).

С помощью дополнительных переменных х₃ и х₄ исходные неравенства преобразуются в уравнения (приводятся к каноническому виду):

5х₁ + 2х₂ + х₃ = 20

8х₁ + 4х₂ + х₄ = 38

Если основные переменные х₁ и х₂ - целые числа, то из уравнений непосредственно следует, что и переменные х₃ и х₄ могут принимать только целочисленные значения.

Задача решается вначале без учета требования целочисленности.

Симплексная таблица имеет следующий вид:

Базис	С	План					θ
Х1	Х2	Х3	Х4
X1→Х3							20/5=4 min
Х4							38/8=4,75
f(x) = 0	-7	-3
X1				2/5	1/5		4:2/5=10
X2→X4				4/5	-8/5		6:4/5=7,5 min
f(x) =28		-1/5	7/5
X1						-1/2
X2		7,5			-2	5/4
f(x) =29,5				1/4

В оптимальном плане Х₁ =1, Х₂ =7,5; максимум целевой функции составляет 29,5. Таким образом, необходимо купить один станок типа А и 7 станков типа В (на 8 станков не хватит ни денег, ни места), тогда объём выпуска продукции составит f(x) =7×1+3×7=28 тыс. единиц продукции.

Найдём целочисленное решение методом Гомори. Для переменной Х₂, получившей нецелочисленное значение в плане, составляем следующее уравнение, непосредственно вытекающее из приведенной симплексной таблицы:

7,5 = Х₂ – 2Х₃ + 1,25Х₄.

Отсюда

Х₂ = 7,5 + 2Х₃ – 1,25Х₄.

Это уравнение, очевидно, должно быть справедливо и для допустимого целочисленного решения задачи.

Поскольку Х₂ - целое число, то целым является и выражение в правой части уравнения; следовательно, величина правой части данного уравнения конгруэнтна нулю:

7,5 + 2Х₃ – 1 ,25Х₄ ≡ 0,

или

–2Х₃ + 1,25Х₄ ≡7,5.

Учитывая приведенные выше свойства конгруэнтности, а также и то, что Х₃ и Х₄ - целые числа, это выражение можно преобразовать в следующее:

{-2}X₃ + {1,25}X₄ ≡{7,5} ;

отсюда получаем:

0,25X₄ ≡ 0,5.

Поскольку X₄ - неотрицательное целое число, имеем:

0,25X₄ = 0,5, или 1,5, или 2,5, ...;

следовательно,

0,25X₄ ≥ 0,5.

Полученное неравенство преобразуется в уравнение и добавляется к исходной системе ограничений, которая содержит теперь следующие три уравнения:

5х₁ + 2х₂ + х₃ = 20

8х₁ + 4х₂ + х₄ = 38

0,25х₄ – x₅ = 0,5.

Повторив процесс решения симплексным методом применительно к расширенной системе ограничений, получим новый оптимальный план, в котором значения переменных, входящих в базис, равны: Х₁ = 2; Х₂ = 5; Х₄ = 2 (остаток свободной площади).

Таким образом, получено оптимальное целочисленное решение задачи: при данных ограничениях максимум производительности (29 тыс. единиц продукции) обеспечивается приобретением 2 машин типа А и 5 машин типа Б.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ

МЕТОД ВЕТВЕЙ И ГРАНИЦ

Этот метод можно применить для решения как полностью, так и частично целочисленных задач дискретного программирования.

Рассмотрим модель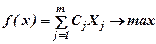

при ограничениях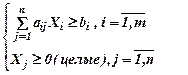

Допустим, что для каждой целочисленной переменной можно задать верхнюю и нижнюю границы, в пределах которых, безусловно, содержатся ее оптимальные значения

H_j ≤ X_j ≤ V_j ; j=1,2,…,k,…,n.

Обычно H_j = 0, но это условие не обязательно. Задача решается симплекс-методом. Если X_k принимает дробные значения, то полагаем, что оптимальное решение задачи, будет удовлетворять линейному ограничению X_k ≤ D_k, либо линейному ограничению X_k ≤ D_k + 1, где D_k=[X_k] – ближайшее целое число в меньшую сторону от значения X_k; D_k + 1 – ближайшее целое в большую сторону от X_k. При этом H_j ≤ D_k≤ V_j– 1. Тогда необходимо решить пару задач линейного программирования симплекс-методом:

А.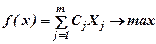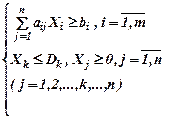

В.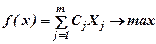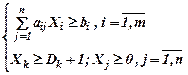

Получаем итерационный процесс, представляемый в виде дерева, вершина которого соответствует решению исходной задачи, а две соединенные с ней ветви являются решениями пары задач линейного программирования А и В. Полученные значения целевых функций при этом могут быть меньше или равны значению целевой функции исходной задачи f(X)_A ≤ f(X)­₀; f(X)_B ≤ f(X)­₀. Каждая из двух новых полученных вершин ветвей может иметь свои дальнейшие ветвления.

1) Итерационный процесс ветвления продолжается до тех пор, пока среди полученных планов не будет получено целочисленное решение, причем значение целевой функции должно быть большим или равным значениям функций целей других ветвящихся вершин.

2) Если на очередном шаге итерации обе задачи имеют нецелочисленные решения, то для дальнейшего ветвления выбирается вершина, соответствующая задача с большим значением функции цели. Для одной из переменных, получивших дробные значения, составляются новые ограничения для следующих задач линейного программирования.

3) Если на очередном шаге итерации одна из задач имеет целочисленное решение, а среди значений переменных во второй задаче имеются дробные, то из них выбирается задача, имеющая наибольшее значение функции цели. Если это задача, получившая целочисленное решение, то процесс заканчивается, если же эта задача с дробными значениями переменных, то для нее производится дальнейший процесс ветвления.

4) Если на очередном шаге итерации одна из задач не имеет решения, а вторая задачи среди значений переменных в получаемом решении имеет дробные величины. Тогда для первой задачи процесс ветвления прекращается, а для дальнейшего преобразования второй задачи выбирается одна из нецелочисленных переменных, для которой составляются дополнительные ограничения для новой пары задач линейного программирования.

5) Если на очередном шаге итерации одна из задач не имеет решения, а для другой получено целочисленное решение, и нет других вариантов с большим целочисленным значением функции цели и для которых можно продолжать ветвление, то процесс заканчивается, а найденное решение является оптимальным целочисленным решением исходной задачи.

Если выбранная задача приводит к обрыву (тупику) или значение функции меньшему, чем в задаче В.1 f(X)_A.4 < f(X)­_В,1., то происходит возврат к задаче В.1 и происходит новое ветвление.

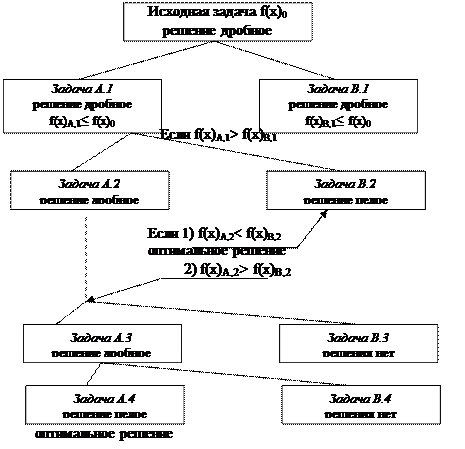Рис.14. Блок-схема алгоритма метода ветвей и границ

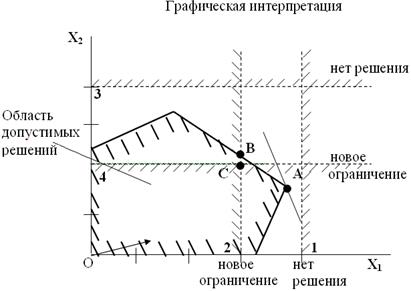
Рис. 15. Метод «ветвей и границ»