Статистическое определение вероятности события. Примеры. Теорема Бернулли (с доказательством)

Статистической вероятностью события А называется относительная частота (частость) появления этого события в n произведенных испытаниях, т.е.

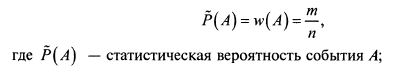
w(A) – относительная частота (частость) события А;

m – число испытаний, в которых появилось событие А;

n – общее число испытаний.

Статистическое определение вероятности, как и понятия и методы теории вероятности, применимы только к тем событиям, которые обладают свойствами:

1) Рассматриваемые события должны быть исходами только тех испытаний, которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий.

2) События должны обладать статистической устойчивостью, или устойчивостью относительных частот. Это означает, что в серии испытаний относительная частота события меняется незначительно.

3) Число испытаний, в результате которых появляется событие А, должно быть достаточно велико, ибо только в этом случае можно считать вероятность события Р(А) приближенно равной ее относительной частоте.

Пример.Английский учёный Пирсон произвел 23000 бросаний монеты, герб появился 11512 раз.

W(A) = 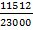= 0.5005

Теорема Бернулли.

Частость события в n повторных независимых испытаниях в каждом из которых оно может произойти с одной и той же вероятностью p, при неограниченном увеличении числа n сходится по вероятности к вероятности р этого события в отдельном испытании:

Cмысл теоремы состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что частость события m/n – величина случайная, как угодно мало отличается от неслучайной величины p – вероятности события, т.е. практически перестает быть случайной.

Доказательство:

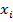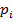	q	p

Отметим, что случайная величина m =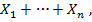

г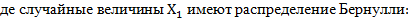

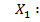
E( 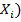= p ; D( 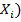= pq

Таким образом, выполняются все условия теоремы Чебышева, т.е.

.

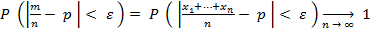Геометрическое определение вероятности. Примеры.

Классическое определение вероятности основывается на том, что число всех возможных случаев конечно. Если распределение возможных исходов испытания непрерывно и бесконечно, то при решении задач часто используется понятие геометрической вероятности.

Полагают, что имеется область Ω и в ней область A. На Ω наудачу бросается точка. Событие А – попадание точки в область А.

Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области Ω, т.е.

P(A) = ;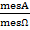

Область Ω может быть одномерной, двумерной, трехмерной и n-мерной.

Пример. В круг радиуса R=50 бросается точка. Найти вероятность ее попадания во вписанный в круг квадрат.

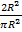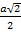Решение. P(A) = = ; ( R = ; a = 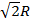)