СХЕМА МЕТОДУ СКІНЧЕННИХ ЕЛЕМЕНТІВ РОЗВ’ЯЗАННЯ ОДНОВИМІРНИХ КРАЙОВИХ ЗАДАЧ
Для конкретизації наведеної вище загальної процедури застосування МСЕ розглянемо одновимірний випадок. Побудуємо схему МСЕ розв’язання задачі Штурма-Ліувілля в області 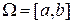 :
:
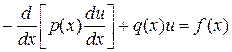 ,
, 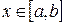 (20)
(20)
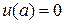 ,
, 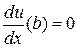 . (21)
. (21)
ДИСКРЕТИЗАЦІЯ ОБЛАСТІ
Для побудови скінченно-елементної сітки поділимо область 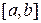 на
на 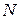 відрізків (скінченних елементів)
відрізків (скінченних елементів) 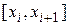 одинакової довжини
одинакової довжини 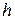 , точками
, точками 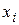 ,
, 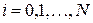 ,
, 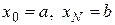 . За вузли СЕ вибиремо кінці відрізка, тобто точки
. За вузли СЕ вибиремо кінці відрізка, тобто точки 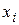 . Отже, кожний СЕ є елементарним відрізком розміру
. Отже, кожний СЕ є елементарним відрізком розміру 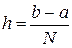 і має два вузли (такий СЕ прийнято називати лінійним одновимірним скінченним елементом), а сітка складається з
і має два вузли (такий СЕ прийнято називати лінійним одновимірним скінченним елементом), а сітка складається з 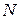 таких елементів, пронумерованих послідовно зліва направо, і
таких елементів, пронумерованих послідовно зліва направо, і 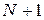 -ого вузла, координати яких можна обчислити за формулою:
-ого вузла, координати яких можна обчислити за формулою: 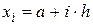 ,
, 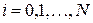 . Як правило, для програмної реалізації схем МСЕ цієї інформації про скінченно-елементну сітку є недостатньо. Як мінімум потрібно задати ще так звану матрицю зв’язності, яка зв’язує номери вузлів та номери СЕ, до яких ці вузли належать. Структура такої матриці може бути такою: кількість стовпців рівна кількості СЕ, кількість рядків – кількості вузлів на одному СЕ, а значення елементів стовпців відповідають номерам вузлів, які відносяться до даного СЕ. На рис.1 зображено фрагмент документа MATHCAD, який містить реалізацію дискретизації області визначення крайової задачі (20)-(21).
. Як правило, для програмної реалізації схем МСЕ цієї інформації про скінченно-елементну сітку є недостатньо. Як мінімум потрібно задати ще так звану матрицю зв’язності, яка зв’язує номери вузлів та номери СЕ, до яких ці вузли належать. Структура такої матриці може бути такою: кількість стовпців рівна кількості СЕ, кількість рядків – кількості вузлів на одному СЕ, а значення елементів стовпців відповідають номерам вузлів, які відносяться до даного СЕ. На рис.1 зображено фрагмент документа MATHCAD, який містить реалізацію дискретизації області визначення крайової задачі (20)-(21).
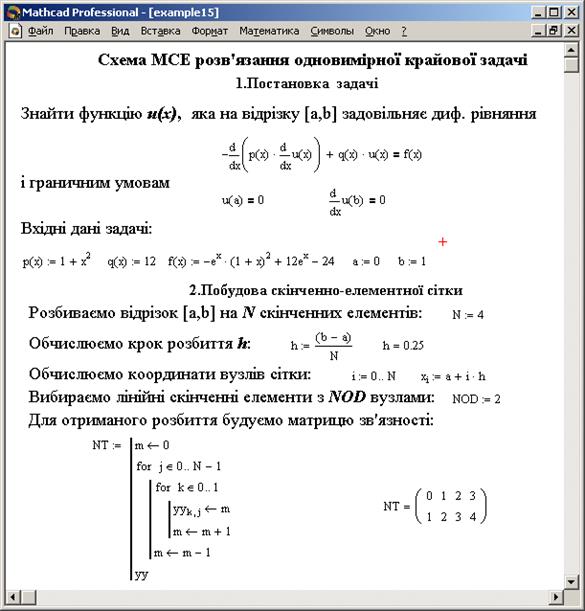
Рис.1. Приклад побудови скінченно-елементної сітки в одновимірному випадку та підготовки інформаційних масивів
Звернемо увагу на двовимірний масив NT, який і відіграє роль матриці зв’язності (тут виведено цей масив для сітки з 4 елементів).
СЛАБКЕ ФОРМУЛЮВАННЯ МЕТОДУ ГАЛЬОРКІНА
Згідно методу Гальоркіна наближений розв’язок 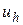 крайової задачі (20)-(21) будемо шукати у вигляді розкладу
крайової задачі (20)-(21) будемо шукати у вигляді розкладу
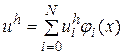 . (22)
. (22)
Тут, і надалі, індекс 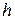 означатиме, що наближений розв’язок шукається на сітці СЕ з кроком розбиття
означатиме, що наближений розв’язок шукається на сітці СЕ з кроком розбиття 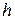 . Підстановка (22) в диференціальне рівняння (20) спричинить появу деякої нев’язки
. Підстановка (22) в диференціальне рівняння (20) спричинить появу деякої нев’язки
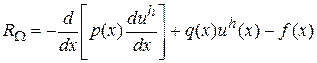 ,
,
на основі якої, за методом Гальоркіна, отримаємо таку систему рівнянь
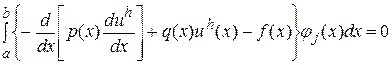 ,
, 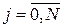 . (23)
. (23)
У (23) під інтеграл входить друга похідна, тому базисні функції повинні бути 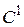 - гладкими на
- гладкими на 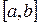 , що є досить жорсткою вимогою. Тому спробуємо послабити цю умову гладкості. Для цього застосуємо правило інтегрування за частинами до першого доданку у рівнянні (23)
, що є досить жорсткою вимогою. Тому спробуємо послабити цю умову гладкості. Для цього застосуємо правило інтегрування за частинами до першого доданку у рівнянні (23)
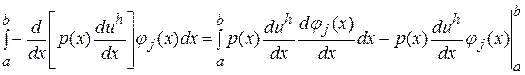 .
.
Врахувавши однорідні граничні умови (21) остаточно отримаємо
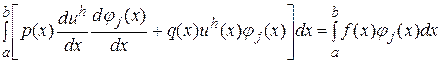 ,
, 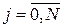 . (24)
. (24)
Рівняння (24) і є слабкою формою рівнянь Гальоркіна, оскільки вони містять під знаком інтеграла вже тільки першу похідну. Отже, тепер достатньо, щоб базисні функції належали 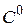 класу гладкості на
класу гладкості на 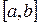 , тобто були просто кусково-неперервними на
, тобто були просто кусково-неперервними на 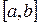 .
.
ПОБУДОВА БАЗИСНИХ ФУНКЦІЙ
Найпростішими базисними функціями МСЕ є кусково-лінійні одновимірні функції, які аналітично задаються співвідношенням
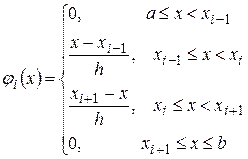 . (25)
. (25)
Легко переконатися, що кусково-лінійні базисні функції (25) володіють властивістю (18), тобто значення кожної функція 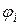 рівне одиниці лише у вузлі
рівне одиниці лише у вузлі 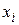 і рівне нулю в усіх інших вузлах. Відповідно, кожна базисна функція
і рівне нулю в усіх інших вузлах. Відповідно, кожна базисна функція 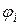 відмінна від нуля лише на тих СЕ, які містять вузол
відмінна від нуля лише на тих СЕ, які містять вузол 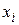 , тобто на елементах з номерами
, тобто на елементах з номерами 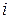 та
та 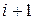 . Більше того, на цих елементах базисна функція
. Більше того, на цих елементах базисна функція 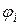 є лінійною. А, отже, базисні функції
є лінійною. А, отже, базисні функції 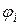 є
є 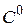 -гладкими на відрізку
-гладкими на відрізку 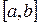 .
.
Тоді глобальна апроксимація 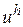 виду (22) стає кусково визначеною, тобто на кожному
виду (22) стає кусково визначеною, тобто на кожному 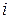 -ому СЕ вона набуває вигляду
-ому СЕ вона набуває вигляду
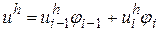 ,
, 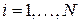 . (26)
. (26)
Приклад програмної реалізації одновимірних кусково-лінійних базисних функцій МСЕ в системі MATHCAD наведено на рис.2. Тут же зображено графіки деяких базисних функцій та їх похідних.
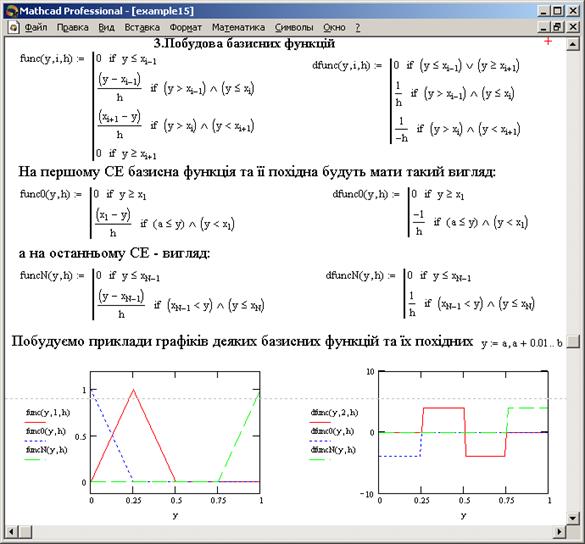
Рис.2. Одновимірні кусково-лінійні базисні функції МСЕ та їх графіки
