Линейного программирования

Графический метод применяется для решения задач линейного программирования малой размерности, когда количество искомых переменных не более 3. На практике этот метод применяют чаще всего для задач с двумя переменными.

В основе графического метода в случае двух (трех) переменных лежат следующие представления. Множество допустимых планов 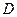можно представить в виде некоторого многогранного выпуклого множества на плоскости (в пространстве). Оптимальное решение, если оно существует и единственно, лежит в угловой точке множества допустимых решений, где пересекаются прямые (плоскости), ограничивающие это множество.

Заметим, что ЗЛП может не иметь решения, когда множество допустимых планов пусто. ЗЛП может иметь бесконечное множество решений, в этом случае решением является часть прямой для двумерной задачи или часть плоскости для трехмерной.

Рассмотрим для определенности задачу максимизации для целевой функции, зависящей от двух переменных:

,

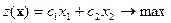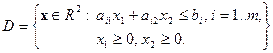(1.12)

Шаг 1. Построение множества допустимых планов.

Каждое 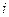-тое ограничение задачи записывается как равенство 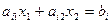. Геометрически полученное уравнение определяет прямую линию, которая делит плоскость на две полуплоскости, в одной из которых выполняется условие 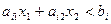, в другой 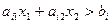. Полуплоскость, для точек которой выполняется требуемое ограничение 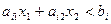, назовем допустимой полуплоскостью.

Если пересечение допустимых полуплоскостей для всех ограничений не пусто, тогда оно представляет собой область допустимых решений, которая называется многоугольником решений. Множество точек, принадлежащих этому многоугольнику, образует множество допустимых планов 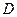(1.12) исходной задачи. При условии не отрицательности переменных многоугольник будет лежать в первой четверти.

Шаг 2.Нахождение оптимального плана.

Необходимо найти точку из многоугольника решений, в которой целевая функция принимает максимальное значение. Если многоугольник решений не пуст и целевая функция на нем ограничена, такая точка всегда найдется, причем она будет лежать в одной из вершин построенного многоугольника решений.

Целевая функция может принимать одно и то же максимальное значение в двух вершинах. В этом случае множество оптимальных решений представляет собой множество точек, лежащих на прямой, соединяющей эти точки.

Для нахождения оптимальной точки рассмотрим целевую функцию задачи 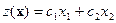. Запишем ее в виде:

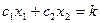, где .

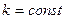Это уравнение задает линии уровня целевой функции, которые являются параллельными прямыми линиями в пространстве переменных .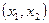

Вектор нормали к прямой 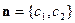к линии уровня целевой функции называется градиентом 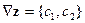. Градиент указывает направление возрастания целевой функции.

Для нахождения точки экстремума графическим методом, необходимо сначала построить линию уровня для некоторого произвольного значения целевой функции. Затем осуществить ее параллельное передвижение в направлении градиента, если решается задача максимизации, и в обратном направлении, при решении задачи минимизации. Смещение производится до тех пор, пока не будет достигнута «последняя» точка области допустимых планов 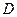. Для задач максимизации (минимизации) такой точке области D соответствует наибольшее из возможных значений линии уровня. Последнее означает, что для нахождения точки экстремума в задаче линейного программирования мы должны сначала построить линию уровня для некоторого произвольного значения целевой функции. Затем необходимо осуществлять ее параллельное передвижение (так, чтобы она оставалась перпендикулярной вектору с ) до тех пор, пока не достигнем такой точки области допустимых планов D , из которой смещение в направлении вектора с было бы невоз­можно. Такой метод решения получил название графического . Заметим, что решение задачи поиска минимума линейной функ­ции осуществляется аналогично, с той лишь разницей, что дви­жение по линиям уровня должно производиться в направлении, обратном градиенту целевой функции, т. е. по вектору (-с ).

Изобразим вектор градиента на плоскости и будем сдвигать линию уровня целевой функции в направлении градиента. Последняя вершина многоугольника решений, с которой пересечется линия уровня и будет оптимальной точкой.

Шаг 3. Нахождение максимального значения функции .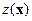

Аналитически оптимальная точка с координатами 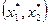находится как точка пересечение двух прямых. Вектор 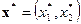является оптимальным планом задачи. Затем вычисляется значение целевой функции в оптимальной точке .

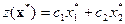Задача. При производстве товаров А и В используются три вида ресурсов: R1, R2, R3. Сведения о количестве ресурсов, необходимых для производства единицы каждого товара, запасе ресурсов и ценах, по которым товары продаются, приведены в табл. 1.3. Найдите оптимальный план, максимизурующий доход.

		Таблица 1.3
	Товары
Ресурсы	A	B	Запас ресурсов
R1
R2
R3
Цена товара	3 у.е.	5 у.е.

1). Искомые переменные задачи:

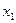— объем производства товара А (шт.);

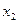— объем производства товара B (шт.);

2). Ограничения задачи.

а) Ограничения на ресурсы. Расход используемых ресурсов не должен превышать их запас.

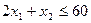, (ресурс R₁),

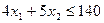, (ресурс R₂), (1.13)

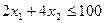, (ресурс R₃).

b) Ограничения на знак. Объемы производства товаров не могут быть отрицательными: , .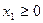

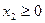3). Целевая функция 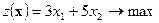максимизирует доход компании.

Запишем математическую постановку задачи максимизации в стандартном виде, в скобках указаны номера ограничений:

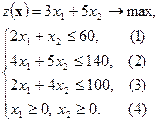
Шаг 1. Построение множества допустимых планов.

Рассмотрим первое ограничение 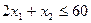, запишем его в виде уравнения 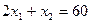, которое задает прямую линию на плоскости. Построим уравнение этой прямой линии в прямоугольной системе координат 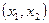. Для этого найдем пересечение данной прямой с осями координат.

Пусть 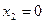, подставив это значение в уравнение прямой найдем 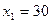. Аналогично, пусть 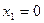, подставив это значение в уравнение прямой найдем 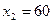. Прямая проходит через две точки с координатами A 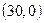и В 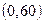. Проведем прямую.

Определим допустимую полуплоскость методом пробной точки. Возьмем точку в начале координат 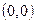и подставим в первое ограничение, получим верное неравенство 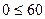. Следовательно, начало координат принадлежит допустимой полуплоскости. В качестве пробной точки можно взять любую точку на плоскости, не принадлежащую данной прямой.

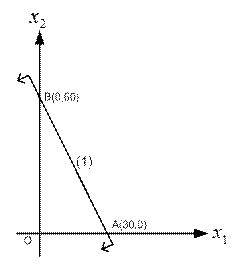
Рис. 1.1. Допустимая полуплоскость для ограничения (1)

Аналогично построим допустимые полуплоскости для ограничений (2) и (3). Условия неотрицательности переменных (4) ограничивают область допустимых планов первой четвертью.

В результате будет построена искомая область допустимого плана 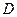, которая ограничена многоугольником OACDE (рис. 1.2). Для точек 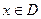выполняются все ограничения задачи.

Осталось найти точку, в которой целевая функция примет наибольшее значение.

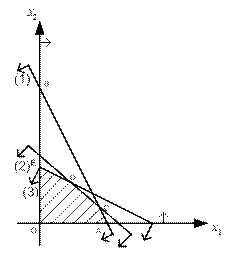
Рис. 1.2. Область допустимого плана OACDE

Шаг 2.Нахождение оптимального плана.

Найдем оптимальный план, то есть точку из многоугольника решений OACDE, в которой целевая функция принимает максимальное значение. Так как полученный многоугольник решений не пуст и ограничен, искомая точка лежит в одной из вершин этого многоугольника.

Построим градиент целевой функции 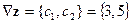, он указывает направление возрастания целевой функции. Любой вектор, коллинеарный градиенту 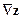также будет указывать направление возрастания целевой функции, по этому, при необходимости вектор 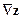можно растянуть или перенести параллельно самому себе (рис. 1.3).

Построим линии уровня целевой функции 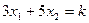, где 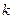— константа. Линии уровня представляют собой прямые линии, перпендикулярные градиенту. Придавая константе 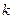различные значения, будем передвигать их в направлении градиента. Последняя вершина многоугольника решений, с которой пересечется линия уровня целевой функции и будет оптимальной точкой.

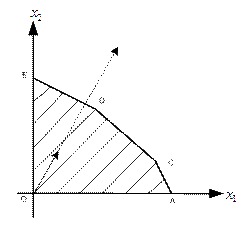
Рис. 1.3. Направление градиента указано пунктиром

На рис. 1.4. изображены пунктиром линии уровня для трех значений константы 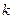. Видно, что оптимальному плану соответствует точка D.

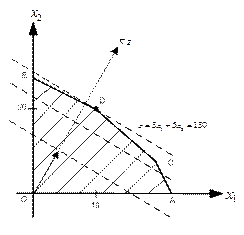
Рис. 1.4. Поиск оптимальной точки

Оптимальная точка D является пересечением двух прямых, соответствующих ограничениям (2) и (3). Поэтому координаты оптимальной точки определяются как решения системы линейных алгебраических уравнений (СЛАУ):

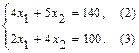(1.14)

Найдем решение СЛАУ (1.14). Второе уравнение можно разделить на 2, получим:

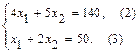
Выразим 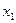из второго уравнения 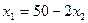и подставим в первое уравнение.

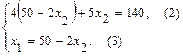
Решим первое уравнение, получим 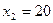, найдем .

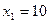Оптимальный план 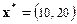. Оптимальное значение целевой функции (доход) составит 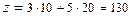у.е.