Дифференциальное уравнение механических колебаний
На всех уровнях организации – от макромолекулярного до популяционного – в биологическихсистемах происходят незатухающие колебания их параметров: ферментативной активности, концентрации метаболитов, параметров, определяющих физиологическое состояние (пульс, смена сна и бодрствования и т.д.). Считается, что любая биологическая система не только может, но и должна быть колебательной. Вот почему колебательным процессам уделяется столь пристальное внимание.
Рассмотрим одну из задач прикладной механики, исследовав, и разрешив ее с помощью линейных дифференциальных уравнений.
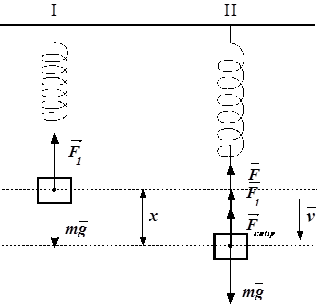 Рис. 6. Рис. 6. |
Пусть, например, тело массой m, подвешено на пружине, жестко закрепленной одним концом (см. рис.6).
Как видно из рис.1 (положение I), вес тела уравновешивается упругой силой пружины, т.е.
F1 = mg
Если оттянуть пружину, то появятся еще две силы: F - восстанавливающая сила пружины, пропорциональная изменению длины пружины и Fсопр - сила сопротивления среды, пропорциональная скорости движения тела.
Равнодействующая сил, расположенных на одной прямой (положение II) определяется как их алгебраическая сумма :
R = F1 + F + Fсопр - mg
Исходя из того, что F1 = mg равнодействующая будет равна
R = F + Fсопр
По второму закону Ньютона
R = ma ; 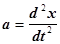
Следовательно,
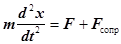 (1)
(1)
Силу F можно определить по закону Гука
F = - kx, (2)
где k - коэффициент жесткости пружины.
Сила Fсопр пропорциональна скорости движения и направлена противоположно ей:
Fсопр= - r v, (3)
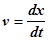 , (4)
, (4)
где r - коэффициент, характеризующий свойства среды оказывать сопротивление движению.
Подставив (2), (3) и (4) в выражение (1) имеем
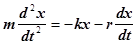 ;
;
Разделим обе части на m, и перенесем все члены в одну сторону, получим
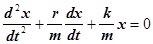 (5)
(5)
Введем следующие обозначения:
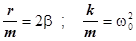 ,
,
Замечание. k и m - величины положительные, следовательно и k/m - тоже величина положительная, поэтому мы вправе обозначить ее квадратом некоторого числа.
Тогда выражение (5) будет иметь вид
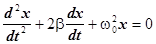 или
или 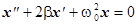 (6)
(6)
Итак, решение нашей задачи свелось к решению линейного однородного дифференциального уравнения.
Воспользуемся нашим алгоритмом решения.
1. Напишем характеристическое уравнение
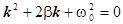
2. Найдем корни этого уравнения
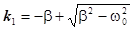 ,
, 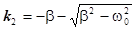
3. Запишем общее решение. Как мы знаем, общее решение зависит от того, какого вида получились у нас корни. Поэтому исследуем каждое решение в отдельности.
Допустим, что
1) b > w0, тогда корни действительные, отрицательные и решение имеет вид
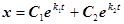
 Рис. 7 График, представляющий решение дифф. уравнения при k1 ¹ k2 Рис. 7 График, представляющий решение дифф. уравнения при k1 ¹ k2 |
Как видно, общее решение выражается через показательные функции. Следовательно, смещение x, при любых C1 и C2 асимптотически стремится к нулю, при t®¥. Графически это выглядит так(рис. 7)
В данном случае колебаний не будет, т.к. силы сопротивления велики по сравнению с коэффициентом жесткости пружины.
2) b = w0, тогда корни характеристического уравнения k1 = k2 = -b.
 Рис. 8. График, представляющий решение дифф. уравнения при k1 = k2 Рис. 8. График, представляющий решение дифф. уравнения при k1 = k2 |
Общее решение, как следует из теории, имеет вид
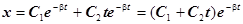
Здесь также смещение стремится к нулю при t®¥, однако не так быстро, как в предыдущем случае (благодаря наличию сомножителя C1 + C2t). Графически это можно представить следующим образом (см. рис.8)
3) b = 0, т.е. отсутствует сила сопротивления, уравнение (6) тогда примет вид
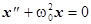 (7)
(7)
Дифференциальное уравнение (7) называется уравнением свободных колебаний. Характеристическое уравнение имеет вид 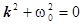 ;
;
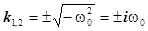
Общее решение 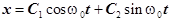 (8)
(8)
Общее решение можно также записать в следующем виде:
x = A cos (w0t + j0) ,
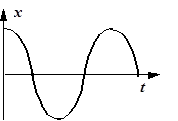 Рис. 9. Гармонический колебательный процесс Рис. 9. Гармонический колебательный процесс |
заменив математические постоянные C1 и C2 величинами A и j0 , имеющими смысловую физическую нагрузку. Эти величины можно легко выразить через C1 и C2 следующим образом: 
Итак, если отсутствуют силы сопротивления, мы получаем гармонический колебательный процесс, где
x - смещение колеблющейся точки от положения равновесия происходит по косинусоидальному закону. При этом w0 - есть круговая (циклическая) частота,
A - амплитуда, т.е. максимальное смещение точки от положения равновесия, j0 - начальная фаза.
4) b < w0, тогда корни характеристического уравнения комплексные
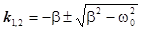
Обозначив 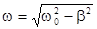 , запишем корни уравнения в виде
, запишем корни уравнения в виде
k1 = - b + i w ; k2 = -b - i w
Тогда решение дифференциального уравнения
x = e -bt (C1 cos wt + C2 sin wt ).
Введя постоянные A0, j0, можно записать решение в виде
x = A0 e -bt cos(wt + j0).
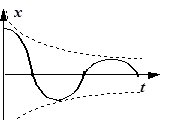 Рис. 10. Затухающий колебательный процесс Рис. 10. Затухающий колебательный процесс |
Мы получили дифференциальные уравнения затухающих колебаний, где 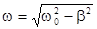 - круговая частота затухающих колебаний, b - коэффициент затухания. Кроме того мы получили зависимость амплитуды затухающих колебаний от времени
- круговая частота затухающих колебаний, b - коэффициент затухания. Кроме того мы получили зависимость амплитуды затухающих колебаний от времени
A (t) = A0 e -bt
В результате данного анализа дифференциального уравнения, соответствующего конкретной задаче механических колебаний выяснили, что колебания будут гармоническими, если корни характеристического уравнения мнимые, или затухающими, если корни характеристического уравнения комплексные. В любом другом случае движения будут апериодическими.
