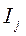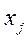Основные принципы имитационного моделирования систем
Определение имитационного моделирования.В сложных системах, характеризующихся многоуровневостью и взаимодействием между собой элементов, каждый из которых также является системой, при традиционном подходе к моделированию исследователь неизбежно сталкивается с огромными трудностями. Основной сложностью оказывается непосредственная формализация и математическое описание общесистемных ситуаций на базе умозрительного анализа связей и зависимостей между элементами системы, тем более, что не всегда для этой цели имеются подходящие математические средства. В таких ситуациях возможен иной путь. На помощь приходят приемы моделирования, которые представляют модель в виде алгоритмической программы для ЭВМ. В этом заключается сущность имитационного моделирования.
имитационное моделирование (ИМ)– это исследование сложной системы на ЭВМ, направленное на получение информации о самой системе. ИМ основано на воспроизведении с помощью ЭВМ развернутого во времени процесса функционирования системы с учетом взаимодействия с внешней средой.
Основными задачами ИМ являются:
· разработка модели исследуемой системы на основе частных имитационных моделей (модулей) подсистем, объединенных своими взаимодействиями в единое целое;
· выбор информативных (интегративных) характеристик объекта, способов их получения и анализа;
· построение модели воздействия внешней среды на систему в виде совокупности имитационных моделей внешних воздействующих факторов;
· выбор способа исследования имитационной модели в соответствии с методами планирования имитационных экспериментов (ИЭ).
Целью ИМ является конструирование имитационной модели объекта и проведение ИЭ над ней для изучения законов функционирования и поведения с учетом заданных ограничений и целевых функций в условиях взаимодействия с внешней средой.
К достоинствам метода ИМ могут быть отнесены:
· проведение ИЭ над имитационной моделью системы, для которой натурный эксперимент не осуществим по этическим соображениям или эксперимент связан с опасностью для жизни, или он дорог, или из-за того, что эксперимент нельзя провести с прошлым;
· решение задач, аналитические методы для которых неприменимы или трудоемки, например, в случае непрерывно-дискретных факторов, случайных воздействий, нелинейных характеристик элементов системы и т.п.;
· возможность анализа общесистемных ситуаций и принятия решения с помощью ЭВМ (в том числе для сложных систем), выбор критерия сравнения стратегий поведения который на уровне проектирования не осуществим;
· сокращение сроков и поиск проектных решений, которые являются оптимальными по некоторым критериям оценки эффективности;
· проведение анализа вариантов структуры больших систем, различных алгоритмов управления, изучение влияния изменений параметров системы на ее характеристики и т.д.
За счет идентичности строения и поведения возможных сочетаний и скачков состояния системы при ИМ имеет место определенное сходство процесса, воспроизводимого ЭВМ, и реального процесса функционирования системы. Конструируя общесистемные ситуации, ЭВМ как бы имитирует явления и события моделируемого процесса.
При экспериментах с имитационными моделями на ЭВМ «проигрываются» различные варианты. Такое «проигрывание» должно быть целенаправленным, организованным и оптимальным (например, в смысле экономии времени исследователя). Для этих целей разработана математическая теория планирования эксперимента, о которой речь пойдет позднее.
Замечательным результатом программной реализации сложных моделей стало уяснение того факта, что алгоритмически можно описывать даже такие системы, которые в силу их сложности не допускают аналитического описания. Это обстоятельство резко расширило класс объектов, доступных для ИМ. В настоящее время методы и способы ИМ широко используются в экономике, химии, агротехнике и в других областях, где практически невозможно получить точное аналитическое решение поставленной задачи. Некоторая потеря достоверности и чистоты результатов в ИМ компенсируется значительным упрощением имитационной модели по сравнению с аналитической.
В обычной постановке ИМ ориентировано на решение задачи анализа и параметрического синтеза из условия получения каких-то оптимальных свойств в исследуемой системе. Например, может решаться задача оценки влияния различных факторов маркетинга на величину получаемой прибыли. Решая эти задачи на имитационной модели можно получить оптимальные значения исследуемых факторов.
Для получения и анализа имитационных моделей в ИМ широко применяется математический аппараткорреляционно-регрессионного анализа.
Общие понятия корреляционно-регрессионного анализа.Статистической называется зависимость между случайными величинами, при которой изменение одной из величин влечет за собой изменение закона распределения другой величины.
В частном случае статистическая зависимость проявляется в том, что при изменении одной из величин изменяется математическое ожидание другой. В этом случае говорят о корреляции или корреляционной зависимости.
Статистическая зависимость проявляется только в массовом процессе, при большом числе единиц совокупности.
регрессия – это односторонняя зависимость между случайными величинами. Она устанавливает соответствие между этими величинами.
Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями. Связи между явлениями могут быть различны по силе. При измерении тесноты связи говорят о корреляции в узком смысле слова. Если случайные переменные причинно обусловлены и можно в вероятностном смысле высказаться об их связи, то имеется корреляция.
Понятия «корреляция» и «регрессия» тесно связаны между собой. В корреляционном анализе оценивается сила, а в регрессионном анализе исследуется форма связи. Корреляция в широком смысле объединяет корреляцию в узком смысле и регрессию.
Любое причинное влияние можно выразить либо функциональной, либо корреляционной связью. Но не каждая функция или корреляция соответствует причинной зависимости между явлениями. Поэтому требуется обязательное исследование причинно-следственных связей.
Исследование корреляционных связей называют корреляционным анализом, а исследование односторонних стохастических зависимостей – регрессионным анализом. Корреляционный и регрессионный анализ имеет свои задачи.
К задачам корреляционного анализа относятся следующие:
1. Измерение степени связности (тесноты, силы) двух и более явлений. Здесь рассматриваются в основном уже известные связи. задача сводится к их подтверждению.
2. Отбор факторов оказывающих наиболее существенное влияние на результативный признак на основании измерения тесноты связи между явлениями.
3. Обнаружение неизвестных причинных связей. Корреляция непосредственно не выявляет причинных связей между явлениями, но устанавливает степень необходимости этих связей и достоверность суждений об их наличии. Причинный характер связей выясняется с помощью логически-профессиональных рассуждений, раскрывающих механизм связей.
Перечислим задачи регрессионного анализа.
1. Установление формы зависимости (линейная или нелинейная; положительная или отрицательная и т.д.)
2. Определение функции регрессии и установление влияния факторов на зависимую переменную. Важно не только определить форму регрессии, указать общую тенденцию изменения зависимой переменной, но и выяснить, каково было бы действие на зависимую переменную главных факторов, если бы прочие не изменялись и если бы были исключены случайные элементы. Для этого определяют функцию регрессии в виде математического уравнения того или иного типа.
3. Оценка неизвестных значений зависимой переменной, то есть решение задач интерполяции и экстраполяции. В ходе экстраполяции распространяются тенденции, установленные в прошлом, на будущий период. Экстраполяция широко используется в прогнозировании. В ходе интерполяции определяют недостающие значения, соответствующие моментам времени между известными моментами, то есть определяют значения зависимой переменной внутри интервала заданных значений факторов.
Итак, корреляционно-регрессионный анализ является одним из важных методов построения математических моделей в экономике. Цель корреляционно-регрессионного анализа – определить общий вид математической модели в виде уравнения регрессии, рассчитать статистические оценки параметров, входящих в это уравнение, и проверить статистические гипотезы о степени зависимости функции от ее аргументов.
Первоначально термин «регрессия» был употреблен Ф.Гальтоном (1886) в теории наследственности. Значительным вкладом в регрессионный анализ явилась разработка метода наименьших квадратов К.Гауссом (1795), А.Лежандром (1806), А.Марковым (1900) и а.Колмогоровым.
Применение статистических методов измерения связей между отдельными факторами особенно необходимо при исследовании экономических процессов, где экспериментальное устранение влияния побочных факторов затруднено или невозможно.
В рамках корреляционно-регрессионного анализа происходит и выбор адекватного эмпирическим данным уравнения регрессии. При этом недостаточно только качественного (логического) анализа. Хотя рабочие гипотезы о возможной форме связи формулировать можно, уравнение регрессии составляется исследователем на основе характера связи между функцией и аргументами. Вопрос о связи решается, как правило, поэтапно.
Статистика разработала множество методов изучения связей, выбор которых зависит от целей исследования и от поставленных задач. Связи между признаками и явлениями ввиду их большого разнообразия классифицируют по ряду оснований.
Связь между двумя признаками (результативным и факторным или двумя факторными) называется парной корреляцией.
Зависимость же результативного и двух или более факторных признаков, включенных в исследование, называется множественной корреляцией.
Корреляционный анализимеет своей задачей количественное определение тесноты связи между признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи количественно выражается величиной коэффициентов корреляции.
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение результативного признака обуславливается влиянием одного или нескольких факторных признаков, а множество всех прочих факторов принимается за постоянные (или усредненные) величины.
Связи между признаками могут быть слабымии сильными (тесными). Количественные критерии оценки тесноты связи оцениваются по шкале Чеддока.
Широко известны два типа связей: функциональные и регрессионные. Если функциональные связи точно выражаются аналитическими выражениями, то регрессионные связи выражаются уравнениями лишь приближенно. В общем случае можно сказать, что связь между функцией и аргументами будет тогда функциональной, когда будут точно учтены все аргументы, определяющие значение функции, что в экономических моделях весьма проблематично.
Корреляционно-регрессивный анализ включает в себя измерение тесноты и направления связи, а также установление аналитического выражения (формы) связи.
Обычно вначале рассматривается линейная форма связи вида
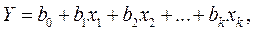 (9.1.1)
(9.1.1)
где xi – факторы, i = 1,2,…,k; так как такая линейная форма связи часто встречается на практике и для нее разработан хороший математический аппарат.
При этом могут решаться следующие задачи:
· установление точности определения коэффициентов регрессии bi в виде значений дисперсий S2(bi) или величины доверительных интервалов;
· установление значимости коэффициентов bi;
· проверка адекватности установленной формы связи экспериментальным данным.
Аппарат корреляционно-регрессионного анализа используется в двух направлениях:
· для проведения статистического анализа результатов наблюдений пассивных экспериментов (экспериментов, в которых независимые переменные xi не могут изменяться экспериментатором, т.е. не регулируются). В результате такого анализа решение вопроса о виде формы связи (уравнения Y = F(X)) не является окончательным, т.е. можно принять в качестве математической модели процесса большое число уравнений регрессии, удовлетворяющих полученным экспериментальным данным;
· совместно с методом наименьших квадратов для планирования статистических экспериментов и анализа результатов. В этом случае планирование экспериментов осуществляется в соответствии с принятым видом уравнения связи Y = F(X).
9.2. Планирование эксперимента в имитационном моделировании
при построении уравнения регрессии
Задача планирования эксперимента.Для получения статистического материала с целью его дальнейшей обработки и получения регрессионной модели исследуемой системы, следует провести серию экспериментов с реальной (если она существует и имеется возможность экспериментирования) или с имитационной (алгоритмической) моделью системы. При этом, естественным является желание провести эксперименты в наиболее короткие сроки и с наименьшими затратами, получая при этом достоверную и достаточно точную информацию.
Планирование эксперимента – это процедура выбора количества и условий проведения опытов, необходимых и достаточных для решения поставленной задачи получения регрессионной модели (РМ) системы с требуемой точностью. Для дальнейшего изложения методики получения РМ сложных экономических систем, воспользуемся введенной ранее моделью «черного ящика» (рис.40), с которой мы и будем проводить имитационные эксперименты.
| |||
 | |||
Рис. 40
Для проведения эксперимента необходимо иметь возможность воздействовать на поведение системы. Все способы таких воздействий обозначим Эти входные воздействия xj назовем факторами или входами «черного ящика».
В экономике принято переменные модели делить на эндогенные (внутренние) и экзогенные (внешние). Значения экзогенных переменных не определяется моделью, их называют также независимыми переменными. Следуя терминологии теории систем, независимые переменные можно разделить на управляемые и неуправляемые. Неуправляемые переменные, например внешнеторговый спрос или курсы валют, могут служить входными переменными системы. Управляемые переменные, например государственные расходы, это переменные, на которые можно влиять с помощью определенных компонент системы.
Значения эндогенных переменных зависят от модели. В системной терминологии их можно разделить на промежуточные («переменные состояния» системы) и на выходные (yi). Кроме переменных мы различаем еще параметры модели, которые остаются постоянными в процессе моделирования.
С точки зрения статистической теории эксперимента фактором называется экзогенная переменная, которая меняется в модели от одного ее варианта к другому В экономических системах факторами могут быть, например, цены, ставки налогов, затраты на продвижение товаров, количество торговых точек и прочее. Параметрами оптимизации могут быть величина прибыли, валовые затраты, доля рынка и т.д.
При планировании эксперимента и обработке его результатов используется математический аппарат дисперсионного и факторного анализа.
Дисперсионный анализ применяется для отсеивания малозначащих факторов в активном эксперименте. Он основан на представлении о том, что значимость фактора xj определяется его вкладом в дисперсию параметра оптимизации yi.
Факторный анализ является естественным развитием дисперсионного анализа. Отличие состоит в том, что оценивается вклад фактора не в дисперсию, а в математическое ожидание параметра оптимизации.
Задача планирования эксперимента возникает в связи с необходимостью построения регрессионной модели (уравнения регрессии) исследуемой системы. Под РМ понимается уравнение, связывающее параметр оптимизации с входными факторами системы. В общем виде это уравнение можно записать так: 
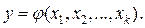 (9.2.1)
(9.2.1)
Функция φ называется функцией отклика системы.
Значения факторов в имитационном эксперименте.Каждый фактор xj может принимать в опыте одно или несколько значений. Такие значения будем называть уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний системы («черного ящика»). Одновременно это есть условия проведения одного из возможных опытов.
Пусть на предварительных этапах исследования установлена область изменения факторов xj :
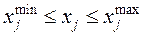 (9.2.2)
(9.2.2)
и координаты нулевого (основного) уровня
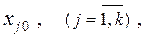 (9.2.3)
(9.2.3)
которые должны лежать внутри области изменения (или определения) факторов. Построение плана имитационного эксперимента сводится к выбору экспериментальных значений факторов xj, симметричных относительно центра эксперимента xj0 (основного уровня). Для каждого фактора выберем два уровня (верхний и нижний), которые он будет принимать в эксперименте. Для этого зададимся интервалом варьирования факторов.
Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычитание – нижний уровни фактора.
Для упрощения записи условий эксперимента и обработки экспериментальных данных введем нормированные значения факторов так, чтобы верхний уровень соответствовал значению +1, нижний –1, а основной имел нулевое значение (см. рис.41), т.е.:
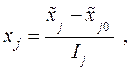 (9.2.4)
(9.2.4)
где 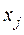 – нормированное значение фактора;
– нормированное значение фактора;
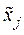 – натуральное значение фактора;
– натуральное значение фактора;
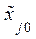 – натуральное значение основного уровня;
– натуральное значение основного уровня;
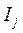 – интервал варьирования j-го фактора;
– интервал варьирования j-го фактора;
|
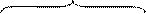
| |
|


 j – номер фактора,
j – номер фактора, 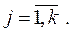
 |  | ||||
| |||||
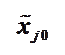
| |||||
| |||||
| |||||
Рис.41
Для качественных факторов, имеющих два уровня, один уровень обозначается +1, а другой –1.
На выбор величины интервалов варьирования 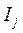 накладываются естественные ограничения. интервал варьирования не может быть меньше той ошибки, с которой экспериментатор фиксирует значение фактора. С другой стороны, интервал не может быть настолько большим, чтобы верхний или нижний уровень фактора оказались за пределами области определения.
накладываются естественные ограничения. интервал варьирования не может быть меньше той ошибки, с которой экспериментатор фиксирует значение фактора. С другой стороны, интервал не может быть настолько большим, чтобы верхний или нижний уровень фактора оказались за пределами области определения.
Если интервал варьирования выбирать достаточно малым и считать, что каждый фактор принимает только два значения, соответствующих верхнему и нижнему уровню:


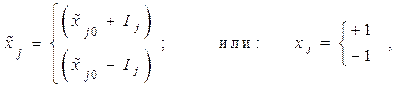 (9.2.5)
(9.2.5)
то методика решения поставленной задачи построения РМ значительно упрощается. Но при этом возможно сильное увеличение размерности задачи.
При решении задачи оптимизации для первой серии экспериментов стремятся выбрать такую подобласть, которая давала бы возможность пошагового движения к оптимуму. В задачах же интерполяции интервал варьирования охватывает всю область определения фактора.
Таким образом, вся область определения факторов 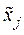 разбивается на ряд интервалов. Полученные для каждого интервала решения (уравнения регрессии) «сшиваются» между собой за счет приравнивания граничных условий в местах стыковки соседних интервалов.
разбивается на ряд интервалов. Полученные для каждого интервала решения (уравнения регрессии) «сшиваются» между собой за счет приравнивания граничных условий в местах стыковки соседних интервалов.
Полный факторный эксперимент.Полный факторный эксперимент (ПФЭ) – это эксперимент, в котором реализуются все возможные сочетания факторов.
Если число значений каждого фактора равно двум (xj= ±1), то мы имеем ПФЭ типа 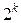 . Тогда, число опытов N , необходимое для реализациивсех возможных сочетаний значений k – факторов, определяется по формуле
. Тогда, число опытов N , необходимое для реализациивсех возможных сочетаний значений k – факторов, определяется по формуле 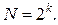
В табл.10 представлена матрица планирования ПФЭ для двух факторов.
Т а б л и ц а 10 Т а б л и ц а 11
| Условия опыта | Результаты опыта | ||
| Номер опыта | 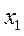 | 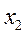 | y |
| +1 –1 +1 –1 | +1 +1 –1 –1 | y1 y2 y3 y4 |
| Номер опыта | 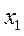 | 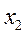 | 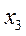 | y |
| +1 –1 +1 –1 +1 –1 +1 –1 | +1 +1 –1 –1 +1 +1 –1 –1 | +1 +1 +1 +1 –1 –1 –1 –1 | y1 y2 y3 y4 y5 y6 y7 y8 |
Для построения матриц планирования ПФЭ с большим числом факторов, чтобы запланировать все возможные реализации факторов, можно использовать правило чередования знаков. Для первого фактора знаки меняются поочередно. Для второго они чередуются через два, для третьего – через четыре, для четвертого – через восемь и т.д. по степеням двойки. Как это выглядит для ПФЭ типа 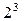 показано в табл.11.
показано в табл.11.
Свойства полного факторного эксперимента типа 2k. Правильно спланированный ПФЭ обладает следующими свойствами:
1. Симметричность относительно центра эксперимента. Это свойство формулируется следующим образом: алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю:
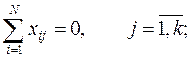 (9.2.6)
(9.2.6)
где j – номер фактора, j =1,2,…, k; i – номер опыта (номер строки матрицы планирования), i =1,2,…, N ; N – число опытов.
2. Условие нормировки: сумма квадратов элементов каждого вектор-столбца равна числу опытов:

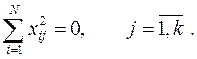 (9.2.7)
(9.2.7)
3. Ортогональность матрицы планирования: сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю:
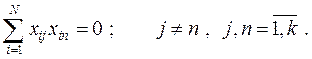 (9.2.8)
(9.2.8)
4. Ротатабельность матрицы планирования: точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации y одинакова на равных расстояниях от центра эксперимента и не зависит от направления (т.е. должен соблюдаться нормальный закон распределения).
Ошибки параллельных опытов.Каждая строка матрицы планирования ПФЭ – это условие опыта, эксперимента с реальной системой или ее имитационной моделью. Каждый эксперимент содержит элемент случайности и неопределенности в силу ограниченности экспериментального материала и возможных ошибок при экспериментировании. Для повышения точности экспериментального материала возникает естественное желание проведения серии повторных параллельных опытов с объектом исследования. Постановка повторных опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроизводимости опыта).
Для повышения точности результата эксперимента и, соответственно, для повышения точности регрессионной модели (РМ), опыт воспроизводится по возможности в одинаковых условиях несколько раз и затем устанавливается среднее арифметическое всех результатов 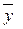
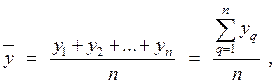 (9.2.9)
(9.2.9)
где n – число параллельных опытов в строке матрицы планирования.
Для определения «грубых» опытов (брака) используется аппарат дисперсионного анализа. Введем понятия среднеквадратического отклонения S (стандарта) результатов параллельных опытов
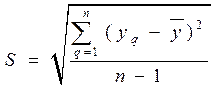 (9.2.10)
(9.2.10)
и дисперсии 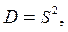 где (n – 1) – число степеней свободы, равное количеству параллельных опытов минус единица.
где (n – 1) – число степеней свободы, равное количеству параллельных опытов минус единица.
Перед подсчетом среднего арифметического 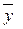 и дисперсии
и дисперсии 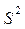 необходимо сначала исключить из рассмотрения результаты грубых опытов. Для определения бракованных результатов можно использовать t-критерий Стьюдента, согласно которому результат опыта должен удовлетворять неравенству
необходимо сначала исключить из рассмотрения результаты грубых опытов. Для определения бракованных результатов можно использовать t-критерий Стьюдента, согласно которому результат опыта должен удовлетворять неравенству
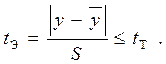 (9.2.11)
(9.2.11)
Значение 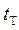 берется из таблицы
берется из таблицы 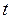 – распределения Стьюдента. Опыт считается бракованным, если экспериментальное значение критерия
– распределения Стьюдента. Опыт считается бракованным, если экспериментальное значение критерия 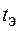 по модулю больше табличного значения
по модулю больше табличного значения 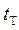 .
.
Пример.Пусть четыре повторных опыта показали следующие значения параметра 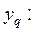 3,580; 2,370; 2,710; 2,761. Результат первого опыта поставлен под сомнение, так как он выделяется на фоне трех остальных опытов.
3,580; 2,370; 2,710; 2,761. Результат первого опыта поставлен под сомнение, так как он выделяется на фоне трех остальных опытов.
Исключим первый опыт из расчета, а по остальным произведем вычисления среднего арифметического 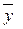 и стандарта S :
и стандарта S :
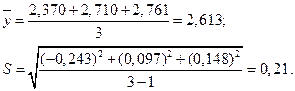
Произведем проверку подозрительного результата по критерию Стьюдента
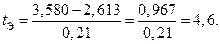
При числе степеней свободы 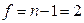 и уровне значимости
и уровне значимости 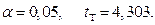 Экспериментальное значение больше табличного, поэтому с вероятностью 0,95 сомнительный результат y = 3,580 можно считать браком.
Экспериментальное значение больше табличного, поэтому с вероятностью 0,95 сомнительный результат y = 3,580 можно считать браком.
Проверка точности эксперимента. После получения результатов всех опытов, проведенных в соответствии с условиями матрицы ПФЭ, часто требуется оценить точность проведенного эксперимента, так как «грубые» опыты в дальнейшем отразятся на адекватности РМ. Точность оценивается путем вычисления дисперсии всего эксперимента, которая получается в результате усреднения дисперсий всех опытов.
дисперсия всего эксперимента также называется дисперсией параметра оптимизации 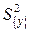 или дисперсией воспроизводимости эксперимента
или дисперсией воспроизводимости эксперимента 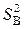 . Если число параллельных опытов n одинаково в каждой строке матрицы планирования, то
. Если число параллельных опытов n одинаково в каждой строке матрицы планирования, то
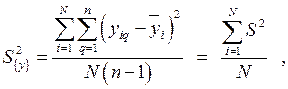 (9.2.12)
(9.2.12)
где 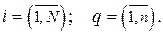
Если число параллельных опытов различное в каждой строке, то
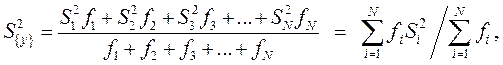 (9.2.13)
(9.2.13)
где 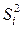 – дисперсия i–го опыта; fi – число степеней свободы в i–м опыте, равное числу параллельных опытов
– дисперсия i–го опыта; fi – число степеней свободы в i–м опыте, равное числу параллельных опытов 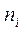 минус единица:
минус единица:
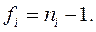 (9.2.14)
(9.2.14)
Формулы (9.2.12) и (9.2.13) могут использоваться только в том случае, если дисперсии однородны, т.е. среди всех суммируемых дисперсий 
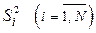 нет таких, которые бы значительно отличались от всех остальных .
нет таких, которые бы значительно отличались от всех остальных .
Проверка однородности дисперсий может производится с помощью различных статистических критериев. Простейшим из них является критерий Фишера, предназначенный для сравнения двух дисперсий. Критерий Фишера (F –критерий) представляет собой отношение большей дисперсии к меньшей. Полученная величина FЭ сравнивается с табличным значением FТкритерия. Для однородных дисперсий должно выполняться неравенство
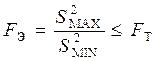 .
.
Если полученное значение дисперсионного отношения больше табличного для соответствующих степеней свободы и выбранного уровня значимости α, значит дисперсии значимо отличаются друг от друга, т.е. они неоднородны и эксперимент проведен грубо. Причиной неоднородности дисперсий может быть, например, разные внешние условия при проведении опытов.
Пример.Пусть 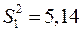 ;
; 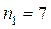 ;
; 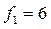 ; и, соответственно:
; и, соответственно:
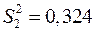 ;
; 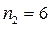 ;
; 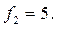
В данном примере отношение дисперсий равно 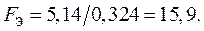 Для уровня значимости
Для уровня значимости 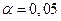 и степеней свободы
и степеней свободы 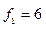 и
и 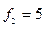 из таблицы F –критерия найдем FТ = 4,40. Экспериментальное значение критерия Фишера значительно превышает табличное, следовательно дисперсии
из таблицы F –критерия найдем FТ = 4,40. Экспериментальное значение критерия Фишера значительно превышает табличное, следовательно дисперсии 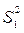 и
и 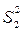 неоднородны и эксперимент носит «грубый» характер.
неоднородны и эксперимент носит «грубый» характер.
Если число дисперсий больше двух, то для оценки точности эксперимента из всех дисперсий выделяется наибольшая и наименьшая. По F –критерию проводится проверка, значимо ли они различаются между собой. Очевидно, что если наибольшая и наименьшая дисперсии не отличаются значимо, то дисперсии, имеющие промежуточные значения, также не могут значимо отличаться.
Следовательно, если выполняется неравенство
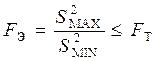 , (9.2.15)
, (9.2.15)
то всю группу дисперсий можно считать однородной, а результаты опытов пригодными для разработки на их основе регрессионной модели исследуемой системы.

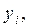
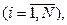 изображают численные характеристики целей исследования. Их называют параметрами оптимизации или выходами «черного ящика».
изображают численные характеристики целей исследования. Их называют параметрами оптимизации или выходами «черного ящика».