Основные законы алгебры множеств
| 1. | 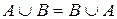 ; (коммутативные ; (коммутативные |  . . | 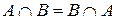 ; законы) ; законы) |
| 2. | 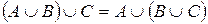 ; (ассоциативные ; (ассоциативные | 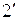 . . | 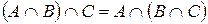 ; законы) ; законы) |
| 3. | 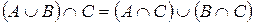 ; (дистрибутивные ; (дистрибутивные | 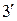 . . | 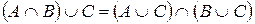 ; законы) ; законы) |
| 4. | 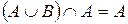 ; (законы ; (законы |  . . | 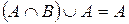 ; поглощения) ; поглощения) |
| 5. | 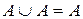 ; (идемпотентные ; (идемпотентные |  . . | 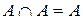 ; законы) ; законы) |
| 6. | 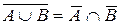 ; (законы ; (законы | 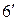 . . | 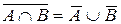 ; де Моргана) ; де Моргана) |
| 7. | 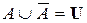 ; ; | 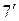 . . | 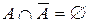 ; ; |
| 8. | 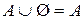 ; ; | 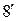 . . | 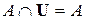 ; ; |
| 9. | 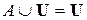 ; ; | 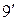 . . | 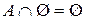 ; ; |
| 10. | 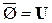 ; ; | 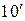 . . | 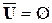 ; ; |
11. 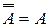 ;
;
12. 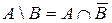 .
.
Доказательство этих формул легко получить универсальным способом доказательства равенства двух множеств. Докажем, например, формулу 5.
□ Если 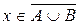 , то
, то 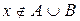 , и, следовательно,
, и, следовательно, 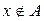 и
и 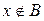 . Но тогда
. Но тогда 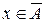 и
и 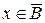 , а поэтому
, а поэтому 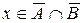 . Значит,
. Значит, 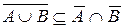 .
.
Обратно, если 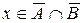 , то
, то 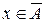 и
и 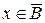 и, следовательно,
и, следовательно, 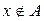 и
и 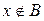 . Но тогда
. Но тогда 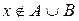 и поэтому
и поэтому 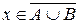 . Таким образом,
. Таким образом, 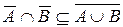 .
.
Из 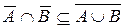 и
и 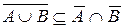 следует, что
следует, что 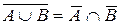 .
.
Пользуясь формулами 1 – 12, можно производить преобразования над множественными выражениями, как над числовыми.
Пример 6. 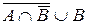
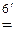
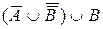
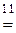
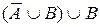
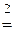
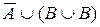
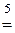
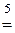
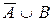 .
.
Заметим, что если в равенствах 1–10 заменить 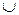 на
на 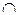 ,
, 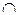 на
на 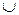 , U на Ø, Ø на U, то получим соответствующие равенства
, U на Ø, Ø на U, то получим соответствующие равенства 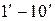 . Отсюда легко вытекает справедливость следующего утверждения, которое называют принципом двойственности теории множеств: если в любом равенстве двух выражений алгебры множеств, не содержащих знака разности, заменить
. Отсюда легко вытекает справедливость следующего утверждения, которое называют принципом двойственности теории множеств: если в любом равенстве двух выражений алгебры множеств, не содержащих знака разности, заменить 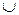 на
на 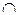 ,
, 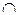 на
на 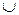 , U на
, U на 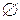 ,
, 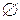 на U, то вновь получится верное равенство.
на U, то вновь получится верное равенство.
Пример 7. Так как 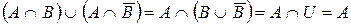 , то справедливо и двойственное равенство:
, то справедливо и двойственное равенство: 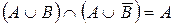 .
.
В дальнейшем нам понадобится еще одна операция над множествами.
Упорядоченная пара – это совокупность двух элементов (не обязательно различных), расположенных в определенном порядке; иначе – это такая совокупность двух элементов, для которых указано, какой из них является первым.
Упорядоченная пара обозначается через 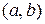 , где элемент a называется первой компонентой, а b – второй компонентой.
, где элемент a называется первой компонентой, а b – второй компонентой.
Упорядоченную пару, например, образуют координаты точки плоскости. Существенным в понятии упорядоченной пары является следующий факт: две упорядоченные пары 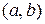 и
и 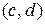 равны (совпадают) тогда и только тогда, когда равны их соответственные компоненты, т.е.
равны (совпадают) тогда и только тогда, когда равны их соответственные компоненты, т.е. 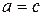 и
и 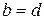 .
.
Точное определение упорядоченной пары дается в аксиоматической теории множеств.
Определение 6. Декартовым (или прямым) произведением множеств  и В называется множество, обозначаемое через
и В называется множество, обозначаемое через 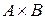 , элементами которого являются всевозможные упорядоченные пары вида
, элементами которого являются всевозможные упорядоченные пары вида 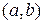 , где
, где 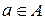 ,
, 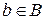 .
.
Символически: 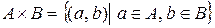 .
.
Пользуясь понятием упорядоченной пары, можно определить понятие упорядоченной тройки. Именно, 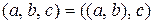 . Аналогично, упорядоченная четверка определяется через упорядоченную тройку и т.д.
. Аналогично, упорядоченная четверка определяется через упорядоченную тройку и т.д.
Аналогично декартову произведению двух множеств  и
и  определяется декартово произведение
определяется декартово произведение 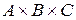 множеств А, В, С – это множество всевозможных упорядоченных троек
множеств А, В, С – это множество всевозможных упорядоченных троек 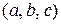 , где
, где 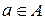 ,
, 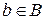 ,
, 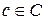 . Точно также определяется декартово произведение
. Точно также определяется декартово произведение 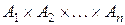 .
.
Пример 8.Если 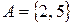 ,
, 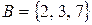 , то
, то
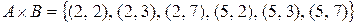 ,
,
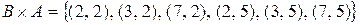 .
.
Пример 9.Если 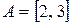 ,
, 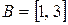 , то
, то
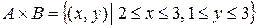 .
.
Графическое изображение:
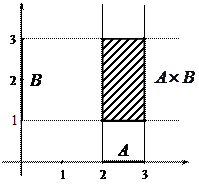 |
Рис. 4.
Из примера 8 видно, что 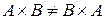 , т.е. декартово умножение множеств не коммутативно. Ясно также, что если
, т.е. декартово умножение множеств не коммутативно. Ясно также, что если  содержит n элементов,
содержит n элементов,  содержит m элементов, то множества
содержит m элементов, то множества 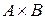 и
и 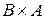 содержат по
содержат по 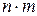 элементов.
элементов.
В частном случае, когда 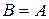 , декартово произведение
, декартово произведение 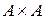 обозначают через
обозначают через 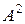 и называют декартовым квадратом множества
и называют декартовым квадратом множества  . Аналогично,
. Аналогично, 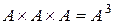 и т.д.
и т.д.
Вопросы для самоконтроля по теме «Множества»
1. Что такое множество?
2. Что называется элементом множества и как символически записывается факт принадлежности или не принадлежности элемента множеству?
3. Что такое пустое множество? Как оно обозначается?
4. Какими способами задаются множества?
5. Что такое подмножество данного множества?
6. Как доказать включение одного множества в другое?
7. Что понимается под универсальным множеством? Как оно обозначается?
8. Что такое булеан множества?
9. Когда говорят, что одно множество строго включается в другое? Как обозначается это факт?
10. Когда два множества называются равными? В чем суть универсального метода доказательства равенства двух множеств?
11. Что означают знаки 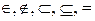 ?
?
12. Принадлежит ли число 3 следующим множествам:
а) 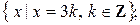 б)
б) 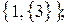 в)
в) 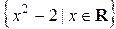 .
.
13. Что называется объединением двух множеств? Как проиллюстрировать эту операцию диаграммой Эйлера-Венна?
14. Что называется пересечением двух множеств? Как проиллюстрировать эту операцию диаграммой Эйлера-Венна?
15. Что называется разностью двух множеств? Как проиллюстрировать эту операцию диаграммой Эйлера-Венна?
16. Что называется дополнением множества? Как проиллюстрировать эту операцию диаграммой Эйлера-Венна?
17. Что называется декартовым произведением двух множеств? Как геометрически проиллюстрировать эту операцию?
18. Что называется симметрической разностью двух множеств? Как проиллюстрировать эту операцию диаграммой Эйлера-Венна?
19. Что означают знаки 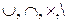 ? Как обозначается дополнение множества?
? Как обозначается дополнение множества?
20. Для множеств 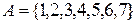 и
и 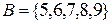 найти
найти 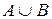 ,
, 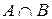 ,
, 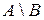 ,
, 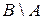 .
.
21. Для множеств 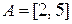 и
и 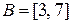 найти
найти 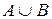 ,
, 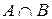 ,
, 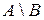 ,
, 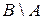 ,
, 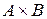 ,
, 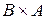 .
.
22. Доказать для любых множеств  и
и  соотношения:
соотношения:
а) 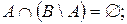
б) 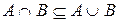 ;
;
в) 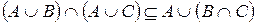 .
.
23. Как записываются свойства операций: законы коммутативности, ассоциативности, идемпотентности, де Моргана, дистрибутивности, поглощения?
24. Как записываются свойства операций объединения и пересечения в связи с пустым и универсальным множествами?
25. Как записываются свойства операции дополнения в связи с пустым и универсальным множествами?
26. Как выражается разность двух множеств через пересечение и дополнение?
27. Доказать свойства:
а) дистрибутивность объединения относительно пересечения;
б) законы де Моргана.
28. Упростить теоретико-множественные выражения при помощи основных свойств операций над множествами:
а) 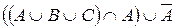 ;
;
б) 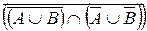 .
.
29. Доказать равенство множеств, используя основные свойства операций над множествами:
а) 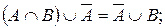
б) 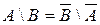 .
.
