Методы решения матричных игр

Я, конечно, живу в постоянной тревоге, играю по самой

маленькой и чего-то жду, рассчитываю, стою по целым

дням у игорного стола и наблюдаю игру.
Ф. М.Достоевский «Игрок»

Наши рассмотрения мы начнем с матричных игр, число стратегий хотя бы одного из игроков в которых равно двум.

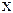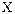1.Для построения решений 2 n и m 2 игр существует эффективный метод, основанный на простых геометрических соображениях. Этот метод называют графическим.
2 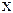n игры.
Пусть 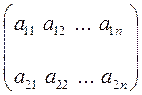- платежная матрица 2 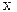n игры.

Согласно теореме о двойном описании игры (теорема 2) нахождение цены игры и оптимального значения р 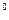для игрока Аравносильно разрешению уравнения

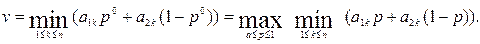
Опишем общую схему, приводящую к искомому результату. Максимум функции 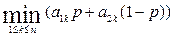(*) проще всего найти, построив ее график. Для этого поступают следующим образом.
Предположим, что игрок А выбрал смешанную стратегию Р = {р, 1 - р}, а игрок В — k-ю чистую стратегию, k: = 1, 2, …, n. Тогда средний выигрыш игрока А в ситуации {Р, k} оказывается равным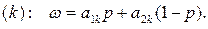
Замечание. На плоскости 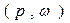уравнение (k) описывает прямую. Тем самым, каждой чистой стратегии игрока В на этой плоскости соответствует своя прямая.

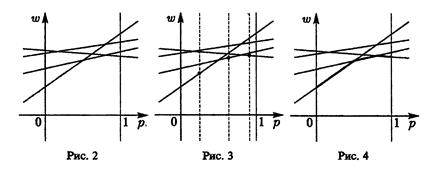
Поэтому сначала на плоскости 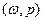последовательно и аккуратно рисуются все прямые 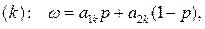=1, 2, ...,n (рис.2). Затем для каждого значения р, 0 ≤ p ≤ 1, путем визуального сравнения соответствующих ему значений 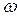на каждой из построенных прямых определяется и отмечается минимальное из них (рис. 3). В результате описанной процедуры получается ломаная, которая и является графиком функции (*) (выделена жирным на рис. 4). Эта ломаная как бы огибает снизу все семейство построенных прямых, и по этой причине ее принято называть нижней огибающей этого семейства. Верхняя точка построенной нижней огибающей определяет и цену игры —v и оптимальную стратегию 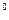Р = {р 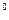, 1 - р 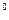} игрока А (рис. 5).
Замечание. Описанная процедура может рассматриваться как некоторый аналог максимального подхода при отсутствии седловой точки.
Опробуем описанную схему решения 2 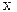n игры на конкретном примере.
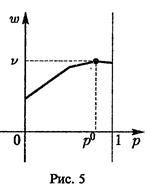Пример 5. Рассмотрим игру, заданную 2 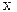6 матрицей

.

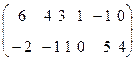Решение.

1) Анализ игры на наличие седловой точки. Нижняя цена игры равна -1, верхняя цена игры равна 1. Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.

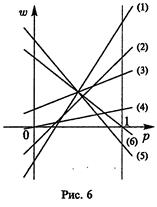2) Вычисление средних выигрышей игрока А (проводится при условии, что игрок В выбирает только чистые стратегии). Из таблицы
р 6 4 3 1 -1 0
1-р -2 -1 1 0 5 4

легко получаем:
(1):
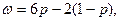
(2):
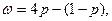
(3):
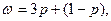
(4):
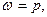
(5):
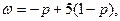
(6):

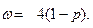
3) Построение нижней огибающей. Аккуратно строим на координатной плоскости 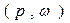все шесть прямых, уравнения которых получены на 2-м шаге (рис. 6), и находим их нижнюю огибающую.

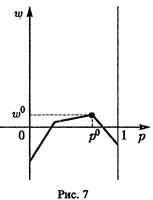4)Отыскание цены игры и оптимальной смешанной стратегии игрока А. При аккуратном построении нижней огибающей нетрудно определить, какие две из построенных шести прямых пересекаются в ее наивысшей точке. В данном случае это прямые (4) и (5), заданные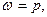 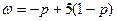соответственно. Решая систему уравнений

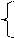
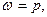
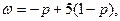
получаем 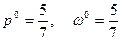(рис.7). Тем самым, цена игры v и оптимальная стратегия Р 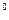игрока А соответственно равны .

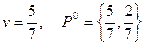Этим заканчивается решение игры для игрока А, поскольку в первую очередь интересует отыскание собственной оптимальной стратегии и ожидаемого наилучшего гарантированного результата.

Замечание. Решающий матричную игру обычно отождествляет себя с одним из игроков (как правило, это игрок А), считая другого своим противником. Это связано еще и с тем, что в некоторых случаях основное внимание уделяется поиску оптимальных стратегий только игрока А, а стратегии противника могут вообще не интересовать исследователя.

Однако в целом ряде случаев оказывается важным знать оптимальные смешанные стратегии обоих игроков.

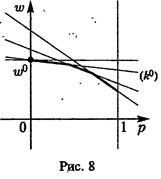Как ищется оптимальная смешанная стратегия игрока А, мы уже описали. Покажем теперь, как отыскать оптимальную смешанную стратегию игрока В. Здесь, в зависимости от формы нижней огибающей, может представиться несколько случаев.

а) Нижняя огибающая имеет ровно одну наивысшую точку :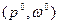

1. Если р 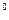= 0 (оптимальная стратегия игрока А -чистая стратегия А 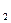), то игроку В выгодно применять чистую стратегию, соответствующую номеру прямой, проходящей через точку (0, 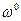) и имеющей наибольший отрицательный наклон (рис. 8).

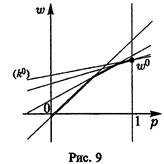
2. Если р 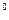= 1 (оптимальная стратегия игрока А -чистая стратегия А 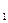), то оптимальной для игрока В является чистая стратегия, соответствующая номеру прямой, проходящей через точку (1, 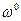) и имеющей наименьший положительный наклон (рис. 9).

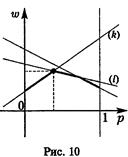3. Если 0 < р 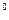< 1, то в наивысшей точке нижней огибающей пересекаются, по меньшей мере, две прямые, одна из которых (k-я) имеет положительный наклон, а другая (l-я) — отрицательный (рис. 10), и оптимальная смешанная стратегия игрока В получается, если положить 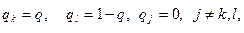где q- решение уравнения .

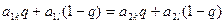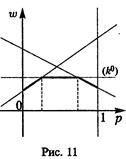б) Нижняя огибающая содержит горизонтальный участок, соответствующий чистой стратегии 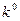игрока В, которая и является оптимальной для него (рис.11).

Пример 5 (продолжение). Покажем теперь, как найти полное решение игры, то есть еще и оптимальную смешанную стратегию 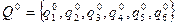игрока В.

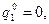
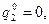
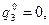
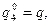
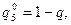
1) Пусть 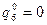, выделив тем самым из шести чистых стратегий игрока В стратеги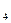и В и В 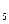, которым соответствуют прямые (4) и (5), определяющие наивысшую точку нижней огибающей.

2) Приравняем любой из двух средних выигрышей игрока В (игрок А выбирает только чистые стратегии), отвечающих предложенной смешанной стратегии

0 0 0 q 1-q 0

6 4 3 1 -1 0

-2 -1 1 0 5 4

к цене игры 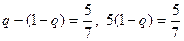и

3) получают один и тот же результат .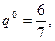

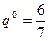Полное решение игры имеет следующий вид
, , .

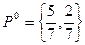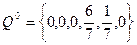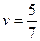2 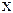m игры.

Пусть теперь в матричной игре две чистые стратегии имеет игрок В, а число чистых стратегий у игрока А произвольно (равно m).
Это означает, что платежная матрица игры имеет вид:

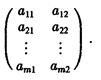
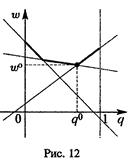Анализ такой игры во многом напоминает рассуждения, описанные для игры 2 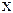n.

Пусть Q={q, 1-q} - произвольная смешанная стратегия игрока В. Если игрок А выбирает i-ю чистую стратегию, i = 1,2,...,m, то средний выигрыш игрока В в ситуации {i, Q} будет равным 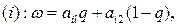i=1,2,...,m.(*)

Зависимость этого выигрыша от переменной q описывается прямой. Графиком функции 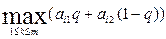является верхняя огибающая семейства прямых (*), соответствующих чистым стратегиям игрока А (рис. 12).

Абсцисса нижней точки полученной ломаной определяет оптимальную смешанную стратегию игрока В, а ордината 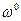- цену игры.

Замечание. Отыскание оптимальной смешанной стратегии игрока А проводится по той же схеме, которая позволяет найти оптимальную смешанную стратегию игрока В в игре 2 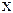n.
Пример 6. 3 х 2 игра задана матрицей .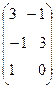

Решение.

1) Анализ игры на наличие седловой точки. Нижняя цена игры равна 0, верхняя цена игры равна 3. Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.

2) Вычисление средних выигрышей игрока В (игрок А выбирает только чистые стратегии). Из таблицы q 1-q
3 -1
1 0
получаем: (1):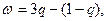
(2):
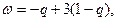
(3): .

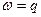3) Построение верхней огибающей. Построим на координатной плоскости 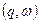все три прямых, а затем и их верхнюю огибающую (рис. 13).

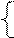
4) Отыскание цены игры и оптимальной смешанной cстратегии игрока В. Нижняя точка верхней огибающей является точкой пересечения прямых (1) и (2). Решая систему уравнений

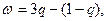
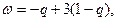
получаем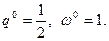

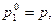
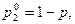
5) Отыскание оптимальной смешанной стратегии игрока А. Полагая 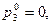приравниваем средние выигрыши игрока А, соответствующие чистым стратегиям игрока В, 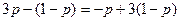и находим 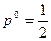. Таким образом, цена игры и оптимальные смешанные стратегии игроков А и В соответственно равны
.

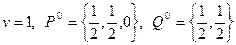m 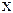n игры.

Решение любой матричной игры может быть найдено методами линейного программирования. При этом требуемый объем вычислений напрямую зависит от числа чистых стратегий игроков (растет с его увеличением и, значит, с увеличением размеров матрицы игры). Поэтому любые приемы предварительного анализа игры, позволяющие уменьшать размеры ее платежной матрицы или еще как-то упрощать эту матрицу, не нанося ущерба решению, играют на практике весьма важную роль.
Правило доминирования.

В целом ряде случаев анализ платежкой матрицы обнаруживает, что некоторые чистые стратегии не могут внести никакого вклада в искомые оптимальные смешанные стратегии. Отбрасывание подобных стратегий позволяет заменить первоначальную матрицу на матрицу выигрышей меньших размеров.

Опишем одну из таких возможностей более подробно.

Пусть А= 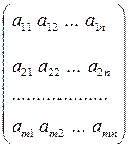- произвольная m 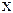n- матрица.
Будем говорить, что i-я строка матрицы А 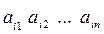не больше j -й строки этой матрицы 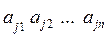, если одновременно выполнены следующие n неравенств 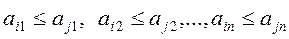. При этом говорят также, что j-я строка доминирует i-ю строку, или что стратегия А 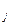игрока А доминирует стратегию А .

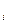Замечание. Игрок А поступит разумно, если будет избегать стратегий, которым в матрице игры отвечают доминируемые строки.

Если в матрице А одна из строк (j -я) доминирует другую строку (i-ю), то число строк в матрице А можно уменьшить путем отбрасывания доминируемой строки (i-й).

Аналогично, можно определять l-й столбец доминирующий k-й столбец, или что стратегия В 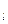игрока В доминирует стратегию В 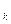. При этом различие бкдет только в знаках неравенств, то есть для k-го столбца 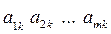меньшего l-го столбца 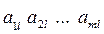неравенства примут вид:

.

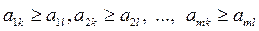Замечание. Игрок В поступит разумно, если будет избегать стратегий, которым в матрице игры отвечают доминируемые столбцы.

Если в матрице А один из столбцов (l-й) доминирует другой столбец (k-й), то число столбцов в матрице А можно уменьшить путем отбрасывания домииируемого столбца (k-го).
Замечание. Оптимальные смешанные стратегии в игре с матрицей, полученной усечением исходной за счет доминируемых строк и столбцов, дадут оптимальное решение в исходной игре: доминируемые чистые стратегии игроков в смешении не участвуют - соответствующие им вероятности следует взять равными пулю.
Пример 7. Рассмотрим игру с матрицей

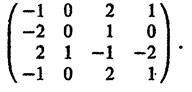
Сравнивая строки матрицы, видим, что 1-я строка совпадает с 4-й строкой, или, что то же, стратегия А 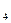дублирует стратегию А . Значит, одну из этих строк можно вычеркнуть, не нанося ущерба решению

Поэлементно сравнивая 1-ю и 2-ю строки, замечаем, что 1-я строка доминирует 2-ю строку, или, что то же, стратегия А 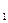доминирует стратегию А 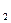. Это вновь позволяет уменьшить число строк матрицы

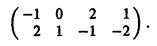
Замечая, что 4-й столбец полученной матрицы доминирует ее 3-й столбец, и вычеркивая его, приходим к игре с 2 х 3-матрицей

Решая эту 2 х 3 игру графическим методом, находим ее решение - цену игры и оптимальные смешанные стратегии игроков А и В:
v = 0,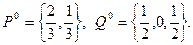

Возвращаясь к исходной 4 х 4 игре, получаем окончательный ответ:
v = 0,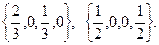

Замечание. При отбрасывании доминируемых строк и столбцов некоторые из оптимальных стратегий могут быть потеряны. Однако цена игры не изменится, и по усеченной матрице может быть найдена хотя бы одна пара оптимальных смешанных стратегий.
Аффинное правило.

При поиске решения матричных игр часто оказывается полезным следующее свойство.

Допустимые преобразования матрицы игры и ее цена. Оптимальные стратегии у матричных игр, элементы матриц А и С которых связаны равенствами 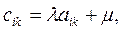i=1,2,…,m; k=1,2,…,n, где λ>0,а µ - произвольно, имеют одинаковые равновесные ситуации (либо в чистых, либо в смешанных стратегиях), а их цены удовлетворяют следующему условию

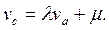
Пример 8. Элементы матриц

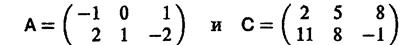
связаны равенством 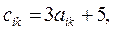i=1,2; k=1,2,3. Поэтому цена игры с матрицей С легко вычисляется 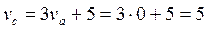(см. пример 7).

Основные этапы поиска решения матричной игры.

1-й этап - проверка наличия (или отсутствия) равновесия в чистых стратегиях (при наличии равновесной ситуации указываются соответствующие оптимальные стратегии игроков и цена игры).

2-й этап - поиск доминирующих стратегий (в случае успеха этого поиска - отбрасывание доминируемых строк и столбцов в исходной матрице игры).

3-й этап - замена игры на ее смешанное расширение и отыскание оптимальных смешанных стратегий и цены игры.

2. Итерационный метод решения матричных игр.

Опишем метод отыскания решения матричной игры (цены игры и оптимальных смешанных стратегий), в известной степени верно отражающий некоторую реальную ситуацию накопления опыта постепенной выработки игроками хороших стратегий в результате многих повторений конфликтных ситуаций. Основная идея метода заключается в том, чтобы мысленно смоделировать реальное практическое «обучение» игроков в ходе самой игры, когда каждый из игроков на собственном опыте прощупывает способ поведения противника и старается отвечать на него наиболее выгодным для себя образом. Иными словами, всякий раз при возобновлении игры игрок выбирает наиболее выгодную для себя стратегию, опираясь на предыдущий выбор противника.

Проиллюстрируем этот метод на примере игры, заданной матрицей

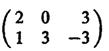
(здесь maxmin = 0, minmax = 2 и, следовательно, седловой точки нет).

Опишем правила выбора ходов игроками, предположив, для определенности, что начинает игрок А:

ход игрока А - стратегия А 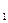- (2 0 3);

игрок В выбирает свою стратегию так, чтобы выигрыш игрока А был минимален:

ход игрока B - стратегия B - ;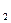

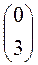игрок А выбирает свою стратегию так, чтобы его выигрыш при стратегии В 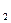игрока В был максимален:

ход игрока А - стратегия А 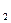- (1 3 - 3);

игрок В выбирает свою стратегию так, чтобы «накопленный» выигрыш игрока А при стратегиях 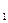А и А ,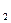

(2 0 3)+(1 3 -3)=(3 3 0), был минимален:
ход игрока В - стратегия В - ;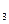

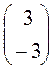игрок А выбирает свою стратегию так, чтобы его «накопленный» выигрыш при стратегиях 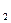В и В 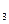игрока В,

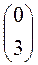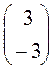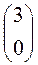+ = , был максимален:

ход игрока А - стратегия А - (2 0 3);

игрок В выбирает свою стратегию так, чтобы «накопленный» выигрыш игрока А при стратегиях А , А и А 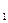: (3 3 0) + (2 0 3) = (53 3), был минимален:

ход игрока В - стратегия В - ;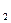

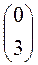и т.д.

Разобьем последовательные ходы игроков А и В на пары (ход игрока А, ход игрока В) и запишем результаты в таблице.

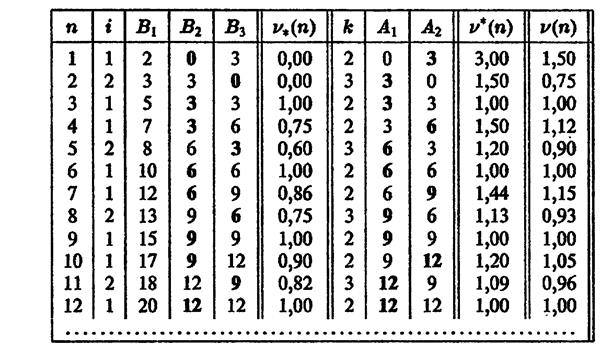
Описание таблицы.

1-й столбец - номер n шага (пары последовательных ходов игроков А и

В),

2-й столбец — номер i стратегии, выбранной игроком А,

3-й столбец — «накопленный» суммарный выигрыш игрока А за первые n

шагов при выборе игроком В стратегии В ,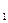
4-й столбец — «накопленный» суммарный выигрыш игрока А за первые n

шагов при выборе игроком В стратегии В ,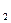
5-й столбец — «накопленный» суммарный выигрыш игрока А за первые n

шагов при выборе игроком В стратегии В ,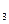

6-й столбец — минимальный средний выигрыш игрока А, равный

минимальному накопленному им выигрышу за первые n

шагов, деленному на число этих шагов,
7-й столбец — номер k стратегии, выбранной игроком В,
8-й столбец — «накопленный» суммарный выигрыш игрока А за первые n

шагов при выборе им стратегии А ,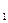

9-й столбец — «накопленный» суммарный выигрыш игрока А за первые n

шагов при выборе им стратегии А ,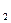
10-й столбец — максимальный средний выигрыш игрока А, равный

максимальному накопленному им выигрышу за первые n

шагов, деленному на число этих шагов,
11-й столбец — среднее арифметическое минимального среднего выигрыша

и максимального среднего выигрыша игрока А.

Решение игры определяется приближенно по окончании любого из шагов. Например, за приближенную цену игры можно взять среднее арифметическое v(n), полученное на n-м шаге. Смешанные стратегии противников определяются частотами появления чистых стратегий.

После 9-го шага имеем v(9) = 1,00. При этом игрок А 6 раз использовал стратегию А 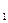и 3 раза стратегию А 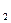. В свою очередь игрок В 6 раз применял стратегию В 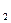, 3 раза стратегию В 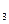, а стратегией В 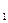не пользовался вообще. Отсюда получаем, что Р 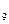= 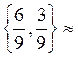{0,67;0,3З}, Q 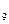= 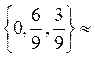{0;0,67;0,33}. Соответственно, после 10-го шага получаем -
v(10) =1,05, P 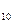= 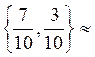{0,7; 0,3}, Q 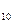= 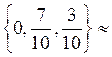{0; 0,7; 0,3}.
Данная игра легко решается графически. Вот точный ответ:
v=1, P = 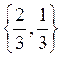, Q =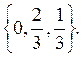
Сравнивая результаты, полученные на 9-м, 10-м, а также 11-м и 12-м шагах:
v(11) =0,96, P 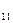= 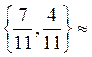{0,64; 0,36}, Q 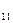= 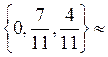{0;0,64;0,36},

v(12) =1,00, P 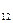= 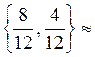{0,67; 0,33}, Q 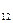= 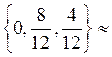{0;0,67;0,33},

заметим, что по мере увеличения числа шагов приближенные значения все меньше отличаются от точных.
Сделаем несколько замечаний.
Замечание 1. При увеличения числа шагов все три величины v 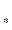(n), v 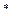(n), v(n) будут приближаться к цене игры v, но среднее арифметическое v(n) будет приближаться к v сравнительно быстрее.
Замечание 2. Хотя сходимость итераций весьма медленна, тем не менее даже такой небольшой расчет всегда дает возможность находить ориентировочное значение цены игры и доли чистых стратегий.
Замечание 3. Сравнительно медленную скорость сходимости можно объяснить целым рядом причин. Укажем одну из них, психологически наиболее интересную. Если, к примеру, игрок А уже получил оптимальную смешанную стратегию, то он не склонен останавливаться на ней. Отнюдь нет - он продолжит попытки выиграть у противника В побольше, особенно если последний еще не достиг оптимальной смешанной стратегия. Таким поведением игрок А может невольно ухудшить свое положение.
Замечание 4. Отметим два основных преимущества описанного метода:
1) итерационный метод прост и одновременно универсален (при его помощи можно легко найти приближенное решение любой матричной игры);
2) объем и сложность вычислений сравнительно слабо растут по мере увеличения числа стратегий игроков (размеров матрицы игры).