Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка – это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Но на самом деле есть некоторые ориентиры для ее применения. Типичными интегралами, где нужно применить универсальную тригонометрическую подстановку, являются следующие интегралы: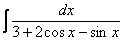 
, 
, 
, 
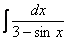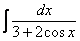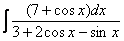и т.д. Приведём примеры использования универсальной тригонометрической подстановки.
Пример 17
Найти неопределенный интеграл
.
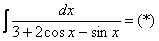Универсальная тригонометрическая подстановка в данном случае реализуется следующим способом. Проведем замену:
.
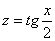Мы используем здесь не букву t, а букву z. Это не какое-то правило, просто привычка.
Здесь удобнее находить дифференциал dx, для этого из равенства 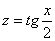, мы выражаем x:
Навешиваю на обе части арктангенс:
.
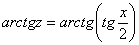Справа арктангенс и тангенс взаимно уничтожаются, получаем:
,
.
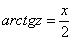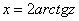Таким образом:
.
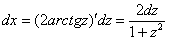На практике можно не расписывать так подробно, а пользоваться готовым результатом: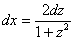 
.
Последнее выражение справедливо только в том случае, если под синусами и косинусами у нас просто «иксы», для интеграла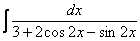 
(о котором мы еще поговорим) всё будет несколько иначе!
При универсальной тригонометрической подстановке синусы и косинусы у нас превращаются в следующие дроби:
, 
.
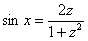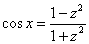Последние равенства основаны на известных тригонометрических формулах:
, 
.
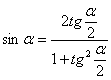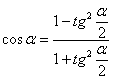Итак, чистовое оформление может быть таким:
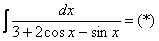
Проведем универсальную тригонометрическую подстановку: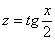 
. Тогда
,
.
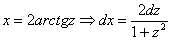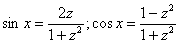Далее, с учётом подстановки:
(1) Производим в исходном интеграле подстановки:
, 
, .
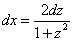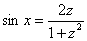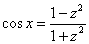(2) Приводим знаменатель к общему знаменателю.
(3) Избавляемся от четырехэтажности дроби, при этом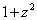 
у нас сокращается. Раскрываем скобки в знаменателе, двойку в числителе выносим за знак интеграла.
(4) Приводим подобные слагаемые в знаменателе.
(5) Интеграл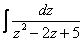 
решается методом выделения полного квадрата. Более подробно с этим методом можно ознакомиться на уроке Интегрирование некоторых дробей. Разложение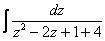 
является подготовкой для осуществления вышеуказанного приёма.
(6) Выделяем полный квадрат и готовим интеграл для интегрирования.
(7) Интегрируем по табличной формуле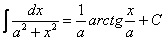 
.
(8) Проводим обратную замену, вспоминая, что 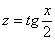. Готово.
Рассмотрим похожий интеграл: .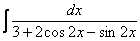
Нет, решать мы его не будем, а просто поймем, как проводить замену.
Здесь тоже проводится универсальная тригонометрическая подстановка: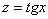 
.
Обратите внимание, что аргумент под тангенсом должен быть в два раза меньше, чем под синусом и косинусом. Формулы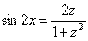 
, 
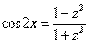сохраняют статус-кво, а вот дифференциал будет немного другой:
.
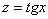
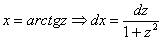Интеграл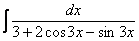 
решается путем замены 
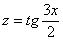и т.д., всё точно так же, единственное отличие, дифференциал будет опять немного другой.
Пример 18
Найти неопределенный интеграл
.
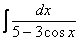Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
С помощью универсальной тригонометрической подстановки решаются и другие интегралы.
Пример 19
Найти неопределенный интеграл
.
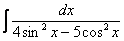Здесь перед применением универсальной тригонометрической подстановки необходимо понизить степени в знаменателе при помощи формул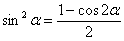 
, 
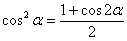. Попробуйте разобраться в данном примере самостоятельно, полное решение и ответ очень близко!
Применение универсальной тригонометрической подстановки часто приводит к длинным и трудоемким вычислениям. Поэтому на практике универсальной тригонометрической подстановки стараются избегать (если возможно). Для этого используют ряд методов и приемов, о которых можно прочитать в статье Сложные интегралы.
Решения и ответы:
Пример 2: Решение:
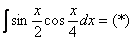
Используем формулу:
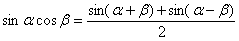
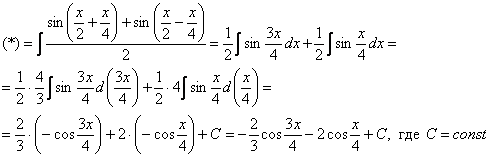
Пример 4: Решение:
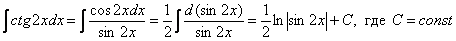
Пример 6: Решение:
Пример 8: Решение:
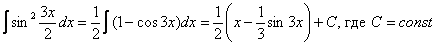
Пример 10: Решение:
Пример 12: Решение:
.
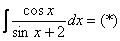Проведем замену:
.
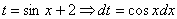
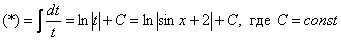Примечание: здесь можно было сделать замену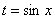 
, но гораздо выгоднее обозначить за t весь знаменатель.
Пример 13: Решение:
.
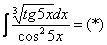Проведем замену:
.
.
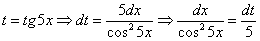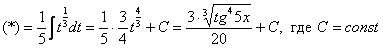Пример 16: Решение:
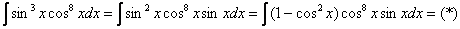Проведем замену: 
.
.
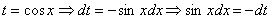Пример 18: Решение:
.
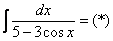Проведем универсальную тригонометрическую подстановку:
.
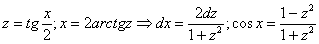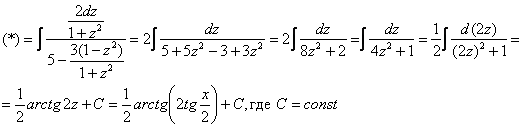
Пример 19: Решение:
.
Универсальная тригонометрическая подстановка:
;
.
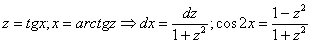