Правила суммы и произведения.(8ч.)
Литература:
1.Л.Г.Петерсон Математика 1,2,3 кл.
В обыденной жизни нам нередко встречаются задачи, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число. Задачи, требующие такого решения называются комбинаторными.
Комбинаторные задачи в начальном курсе систематически решаются как правило, методом перебора. Для облегчения этого процесса нередко используются таблицы и графы. В связи с этим учителю начальных классов необходимы определенные навыки решения комбинаторных задач. Прежде всего, он должен, решая несложные комбинаторные задачи, уметь грамотно осуществлять перебор всевозможных вариантов и при этом быть уверенным в том, что перебор осуществлен правильно. Учителю надо знать общие правила комбинаторики (суммы, произведения), некоторые виды комбинаций, число которых может быть подсчитано с помощью формул.
Впервые во 2 классе II часть Ур. 37-42. К настоящему времени дети уже достаточно подготовлены к усвоению мысли о целесообразности упорядоченного перебора правила суммы и произведения.
1. Правило суммы – для нахождения числа элементов в объединении непересекающихся конечных множеств. Если объект а можно выбрать m способом, а объект в – k способом, то выбор» либо а, либо в» –( m + k) способом.
Задача: На тарелке лежит 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
Так как в задаче речь идет о выборе либо яблок, либо апельсинов, то согласно правилу суммы, можно осуществить 5 + 4 = 9 способом.
2. Правило произведения – для нахождения элементов в декартовом произведении. Если объект а можно выбрать m способом, а объект а, в – k способом, то пару (а,в)можно выбрать – m х k способом.
Задача1: На тарелке 5 яблок и 4 апельсина. Сколькими способами можно выбрать пару плодов из апельсинов и яблок.
Решение, т.к. речь идет о выборе пары (яблоки, апельсины), то согласно правилу произведения 4 х 5 = 20 способов.
Задача 2: Сколько трехзначных чисел можно составить, используя цифры 7,4,5?
Решение: О подсчете числа наборов из трех элементов (кортеш), согласно правилу произведения получим 3 х 3 х 3 = 27 способов.(т.к. цифры в записи числа могут повторяться, то цифру сотен, цифру десятков и цифру единиц можно подобрать 3 разными способами каждую.)
Задача. Сколько всего четырехзначных чисел можно составить из цифр 0 и 3?
Решение. Запись четырехзначного числа представляет собой упорядоченный набор (кортеж) из четырех цифр. Первую цифру - цифру тысяч можно выбрать только одним способом, так как запись числа не может начинаться с нуля. Цифрой сотен может быть либо ноль, либо три, т.е. имеется два способа выбора. Столько же способов выбора имеется для цифры десятков и цифры единиц.
Итак, цифру тысяч можно выбрать одним способом, цифру сотен - двумя, цифру десятков - двумя, цифру единиц - двумя. Чтобы узнать, сколько всего четырехзначных чисел можно составить из цифр 0 и 3, согласно правилу произведения, способы выбора каждой цифры надо перемножить: 1х2х2х2 = 8.
Таким образом, имеем 8 четырехзначных чисел.
Задача . Сколько трехзначных чисел можно записать, используя цифры 0, 1, 3, 6, 7 и 9, если каждая из них может быть использована в записи только один раз?
Решение. Так как запись числа не может начинаться с нуля, то цифру сотен можно выбрать пятью способами; выбор цифры десятков можно осуществить также пятью способами, поскольку цифры в записи числа не должны повторяться, а одна из шести данных цифр будет уже использована для записи сотен; после выбора двух цифр (для записи сотен и десятков) выбрать цифру единиц из данных шести можно четырьмя способами. Отсюда, по правилу произведения, получаем, что трехзначных чисел (из данных шести цифр) можно образовать 5х5х4= 100 способами.
Дерево возможностей – наиболее универсальное средство для поиска решения.
Т.к. детям самим сложно отыскать логику, то надо показать детям использование «дерева».
    * * | ||||
 0 0 | 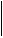 1 1 | 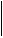 2 2 | 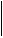 3 3 | |
| II |
Типовые примеры
Пример. В вазе для фруктов лежало 6 яблок, 5 груш и 4 персика. Сколькими способами можно выбрать один плод для угощения?
Решение. В задаче речь идет о выборе «либо яблоко, либо груша, либо персик». Число способов осуществить такой выбор определяется по правилу суммы:
6 + 5 + 4 = 15 (способов).
Пример. Нужно купить подарок для первоклассника, состоящий из ранца, пенала, подставки для книг и дневника. Сколькими способами это можно сделать, если магазин предлагает 4 вида ранцев, 5 видов пеналов, 3 вида подставок и 2 вида дневников?
Решение. Ответ на вопрос задачи сводится к подсчету числа способов осуществить выбор «и ранец, и пенал, и подставка, и дневник». Очевидно, что задача решается по правилу произведения, а значит, подарок можно составить
4 • 5 • 3 • 2 = 120 (способами).
Упражнения:
1. Сколько различных двузначных чисел можно записать, используя цифры 3, 4, 5 и 6? Сколько различных двузначных чисел можно записать, используя при записи числа каждую из указанных цифр только один раз? Запишите эти числа.
4. Сколько трехзначных чисел можно составить из трех различных, не равных нулю цифр? Зависит ли результат от того, какие цифры взяты? Укажите какой-нибудь способ перебора трехзначных чисел, при котором ни одно число не может быть пропущено.
Сколько всевозможных трехзначных чисел можно составить из цифр 1, 2, 3 и 4 так, чтобы цифры в записи числа не повторялись? Изменится ли решение этой задачи, если вместо цифры 4 будет дана цифра О?
4.  Сколько всевозможных четырехзначных чисел можно составить, используя для записи цифры 1, 2, 3 и 4? Какова разность между самым большим и самым маленьким из них?
Сколько всевозможных четырехзначных чисел можно составить, используя для записи цифры 1, 2, 3 и 4? Какова разность между самым большим и самым маленьким из них?
5. Сколько пятизначных чисел, первые (слева) три цифры которых 2, 3 и 4, можно составить из цифр 1, 2, 3, 4, 5? Изменится ли ответ в этой задаче, если цифры в записи числа не будут повторяться?
6. Из цифр 0, 1, 2, 3, 4 составляют всевозможные пятизначные числа, причем так, что в записи каждого числа содержатся все данные цифры. Сколько можно составить таких чисел? Чему будет равна разность между наибольшим и наименьшим из полученных чисел?
7. Сколько натуральных чисел, меньших 1000, можно записать, используя цифры 7, 4 и 5? Сколько среди них четных? Нечетных? Кратных 5?
