Тема 1.1.5 Разбиение на части
Под классификацией в науке понимают логическую операцию, состоящую в разбиении всего множества по каким – либо свойствам на подмножества, при этом должны выполняться условия:
1) ни одно из подмножеств не пусто;
2) подмножества попарно не пересекаются;
3) объединение всех подмножеств совпадает с самим множеством.
Классификацию можно выполнить:
1) путем указания признака (класс имеющих и не имеющих указанный признак).
Если на множестве Х задано одно свойство, то это множество разобъется на 2 класса (I – объекты, которые обладают эти свойством , II – не обладают).
Например, множество натуральных чисел по признаку быть двузначным числом, или быть кратным 3.
Классификация – это наведение порядка в множестве (все «вещи» раскладываются по «полочкам»). Ни один предмет не может находиться одновременно на 2-х полках, кроме того, все до одного предмета должны быть убраны).
Упражнения
1. Даны два множества: X = {2, 4, 6} и Y = {0, 2, 4, 6, 8}.
Верно ли что:
а) множества X и Y пересекаются;
б) множество X является подмножеством множества Y;
в) множество Р = {4, 0, 6, 8, 2} равно множеству У?
2. Из множества К = {216, 546, 153, 171, 234} выпишите
числа, которые:
а) делятся на 3; б) делятся на 9;
в) не делятся на 4; г) не делятся на 5.
Есть ли среди полученных подмножеств такое, которое равно множеству К!
3. Изобразите при помощи кругов Эйлера отношения между множествами Си D, если:
а) С - множество двузначных чисел,
D = {3,43, 34, 56, 103};
б) С - множество двузначных чисел,
D - множество четных натуральных чисел;
в) С - множество двузначных чисел,
D - множество трехзначных чисел;
г) С - множество двузначных чисел,
D - множество натуральных чисел, не меньших 10.
4. Какое из данных множеств является подмножеством другого:
а) А - множество натуральных чисел, кратных 2,
В - множество натуральных чисел, кратных 6,
С - множество натуральных чисел, кратных 3.
б) А - множество треугольников,
В - множество прямоугольных треугольников, С- множество остроугольных треугольников.
Пересечение множеств:
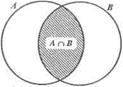
1) Пусть даны два множества: А = {2, 4, 6, 8} и В = {5, 6, 7, 8, 9}. Образуем множество С, в которое включим общие элементы множеств А и В, т.е. С = {6, 8}. Так полученное множество С называют пересечением множествА и В.
 |
| ( |
Определение. Пересечением множеств А иВ называется множество, содержащее те и только те элементы, которые принадлежат множеству А и множеству В. Пересечение множеств А и В обозначают А 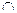 В. Таким образом, по определению, А
В. Таким образом, по определению, А 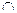 В = {х|х
В = {х|х  А и х
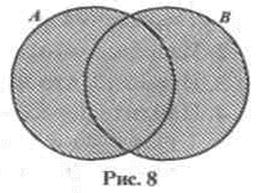
А и х 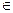 В}. Если изобразить множества А и В при помощи кругов Эйлера, то пересечением данных множеств является заштрихованная область .
В}. Если изобразить множества А и В при помощи кругов Эйлера, то пересечением данных множеств является заштрихованная область .
В том случае, когда множества А и В не. имеют общих элементов, говорят, что их пересечение пусто и пишут: А 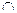 В = 0.
В = 0.
2) Если множества заданы характеристическими свойствами своих элементов?
Найдем, например, пересечение множества А - четных натуральных чисел и множества В- двузначных чисел. Характеристическое свойство элементов множества А - «быть четным натуральным числом», а характеристическое свойство элементов множества В- «быть двузначным числом». Тогда, согласно определению, элементы пересечения данных множеств должны обладать свойством «быть четными натуральными и двузначными числами». Таким образом, множество А 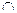 В состоит из четных двузначных чисел (союз «и» в данном случае можно опустить). Полученное множество не пусто. Например, 24
В состоит из четных двузначных чисел (союз «и» в данном случае можно опустить). Полученное множество не пусто. Например, 24 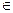 А
А 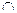 В, поскольку число 24 четное и двузначное.
В, поскольку число 24 четное и двузначное.
Упражнения
1. Найдите пересечение множеств А и В, если:
a)A = {a,b,c,d,e,f},B={b,e,f,k}
б) А = {26,39,5,58, 17,81}, В= {17,26,58}.
в) А = {26,39,5,58, 17, 81}, В= {17, 26, 58, 5, 39, 81}.
2.Из каких элементов состоит пересечение множества букв в слове «математика» и множества букв в слове «геометрия»?
3.М- множество однозначных чисел, Р- множество нечетных натуральных чисел. Из каких чисел состоит пересечение данных множеств? Содержатся ли в нем числа -7 и 9?
4.Начертите два треугольника так, чтобы их пересечением: а) был треугольник; б) был отрезок; в) была точка.
Объединение множеств
1) Пусть даны два множества: А = {2, 4, 6, 8} и В = {5, 6, 7, 8, 9}. Образуем множество D, в которое включим элементы, принадлежащие хотя бы одному из данных множеств, т.е. множеству А или множеству В: D = {2, 4, 6, 8, 5, 7, 9}. Так полученное множество D называют объединением множеств А и В.
| ( |
Определение. Объединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В.
Объединение множеств А и В обозначают А 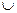 В. Таким образом, по определению, А и В = {х \ х
В. Таким образом, по определению, А и В = {х \ х 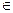 А или х
А или х 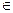 В}.
В}.
РИСУНОК:
Если множества заданы характеристическими свойствами их элементов, то надо использовать союз « или».
2)Найдем, например, объединение множества А - «быть четным натуральным числом», а свойство элементов множества В- «быть двузначным числом», то в объединение данных множеств войдут числа, характеристическое свойство которых- «быть четным натуральным или двузначным числом». Тогда Д=А 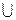 В
В
Пример: 8 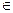 А
А 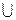 В , 36
В , 36 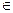 А
А 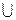 В
В
3)Рассмотрим теперь случай: А 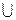 В=А,т.е. В
В=А,т.е. В 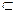 А , характеристическое свойство элементов множества А и В будет таким, как и свойство элементов множества А.
А , характеристическое свойство элементов множества А и В будет таким, как и свойство элементов множества А.
Упражнения
1. Найдите объединение множеств А и В, если:
а) А = {а, Ъ, с, d, e,f), В = {Ь, e,f, k).
6)А = {26,39,5,58, 17, 81}, В= {17,26,58}.
в)А = {26,39,5,58, 17, 81}, В= {17,26,58,5,39,81}.
2. Из каких элементов состоит объединение множества букв м слове «математика» и множества букв в слове «геометрия»?
3. М - множество однозначных чисел, Р- множество нечетных натуральных чисел. Из каких чисел состоит объединение данных множеств? Содержатся ли в нем числа -7 и 9?
4. Используя координатную прямую, найдите объединение множеств решений неравенств, в которых х- действительное число:
а) х > -2 и х > 0; . в) х 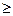 5 и х < -7,5;
5 и х < -7,5;
б) х > -3,7 и х 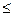 4; г) -2 <х < 4 и х
4; г) -2 <х < 4 и х 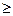 -1;
-1;
д)-7 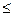 х
х 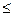 5 и -6
5 и -6 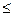 х
х 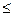 2.
2.
8. Начертите две фигуры, принадлежащие объединению множеств С и D, если:
а) С-множество ромбов,
D - множество прямоугольников;
б) С - множество равнобедренных треугольников,
D - множество прямоугольных треугольников.
