Нестационарные временные ряды
Если временной ряд содержит, например, некоторый тренд, то требование постоянства дисперсии, среднего и ковариации нарушается, и мы имеем дело с нестационарным процессом, или процессом случайного блуждания. На практике временной ряд xt можно субъективно определить как нестационарный при помощи графика временного ряда и его коррелограмм. Если на них обнаруживаются:
1) тренд;
2) детерминистическая периодичность;
3) гетероскедастичность;
4) изменяющаяся автокорреляция,
то имеются веские причины предполагать, что лежащий в основе процесс является нестационарным. Теоретически он нестационарен, если среднее или дисперсия, или ковариация случайного процесса, сгенерировавшего этот временной ряд, изменяются во времени.
Как правило, временные ряды, характеризующие экономические явления, отличаются нестационарностью. Это связано с некоторыми свойствами экономических временных рядов, прежде всего с наличием тренда. Очевидно, что при наличии трендовой компоненты сложно утверждать, что среднее значение ряда, а также его дисперсия и автоковариация не зависят от времени, следовательно, ряд нестационарен. Временные ряды могут иметь как строго возрастающий (убывающий) тренд, так и заметные колебания на фоне общего тренда. Подобное поведение характерно для показателей ВВП, а также для показателей инфляции и процентной ставки.
Для некоторых нестационарных временных рядов характерно случайное блуждание. Обычно такие временные ряды не выказывают тенденции ни к возрастанию, ни к убыванию. Временной ряд может возрастать или убывать со временем и не сохранять среднего значения в долгосрочном периоде.
Еще одной из причин, вызывающих нестационарность временных рядов, является высокая инерционность внезапного воздействия (шока) на временной ряд. Во время экономического спада или бума основные макроэкономические показатели претерпевают сильные изменения и остаются на новом уровне в течение длительного промежутка времени, не возвращаясь к своему прежнему положению.
Относительно длинные временные ряды, характеризующие, например, процессы инфляции или уровень инвестиций, в некоторых случаях можно охарактеризовать как условно гетероскедастичные. Это означает, что в долгосрочном периоде (на протяжении нескольких десятков лет) дисперсия ряда постоянна, но в рамках данного периода имеются более короткие отрезки времени (продолжительностью в несколько лет), на протяжении которых дисперсия явления относительно высока.
Идентификация рядов, основанная на проверке постоянства среднего, дисперсии и ковариации, невозможна, так как априори структура ряда неизвестна.
Для получения критерия, который можно было бы использовать для выявления нестационарности рядов, рассмотрим авторегрессионный процесс Yt первого порядка:
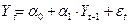. (3.6)
Несложно проверить, что при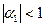 
условия выполняются, а при 
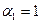- не выполняются, т.е. в первом случае можно говорить о стационарном, а во втором случае - о нестационарном процессе yt, поэтому нестационарные процессы называют также процессами единичного корня.
Между стационарными и нестационарными временными рядами имеется существенное отличие. Единовременное шоковое воздействие на стационарный ряд носит временный характер. Со временем эффект рассеивается, и значения временного ряда возвращаются к своему долгосрочному среднему значению. Следовательно, долгосрочный прогноз стационарного ряда сходится к безусловному среднему. Для облегчения идентификации стационарных рядов будем использовать следующие свойства:
1. Уровни ряда колеблются вокруг постоянного долгосрочного среднего значения.
2. Временной ряд имеет постоянную, не зависящую от времени дисперсию.
3. Временной ряд имеет теоретическую коррелограмму, которая убывает при возрастании длины лага.
С другой стороны, нестационарные ряды обязательно имеют постоянную компоненту, среднее и/или дисперсия зависят от времени. Перечисленные ниже свойства помогут идентифицировать нестационарные временные ряды.
1. В долгосрочном периоде не существует постоянного среднего значения, к которому возвращаются значения временного ряда.
2. Дисперсия зависит от времени и по мере увеличения времени растет до бесконечности.
3. Теоретическая автокорреляция не сокращается, но для наблюдений, ограниченных некоторыми пределами, медленно затухает.
Для формального определения стационарности ряда эти свойства не подходят. В основу тестов на идентификацию временных рядов положена проверка условия равенства или неравенства параметра α1 из уравнения (10.1) единице. Это так называемые тесты единичного корня.