Пример задачи о раскрое

Пример

Для изготовления брусьев трех размеров: 0.6 м, 1.5 м и 2.5 м в соотношении 2 : 1 : 3 на распил поступают бревна длиной в 3 м. Определить план распила, обеспечивающий максимальное число комплектов.

Решение. Прежде всего определим всевозможные способы распила бревен, указав сколько соответствующих брусьев при этом получается.

Способы Распила (i)	Получаемые брусья	Количество бревен, распиленных по i-му способу
0.6	1.5	2.5
		------	------	X1
			------	X2
	------		------	X3
	------	------		X4

Теперь составляем математическую модель, приняв, что всего поступает на распил A бревен: максимизировать число комплектов z=x при условиях, что все бревна должны быть распилены (x₁+x₂+x₃+x₄=a) и что число брусьев каждого размера должно удовлетворять условию комплектности:

5x₁+2x₂=2x; x₂+2x₃=1*x; x₄=3x.

Из последнего равенства, определив x= x₄ и исключив x из остальных выражений, придем окончательно к следующей задаче:

z=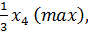

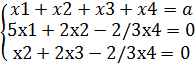
x₁≥0, x₂≥0, x₃≥0, x₄≥0.

После решения ее симплекс методом получим оптимальное решение задачи X_опт= ( 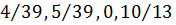) и z_max= .

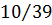Таким образом, 10,2% общего числа поступающих бревен следует распилить по 1-му способу, 12,8% -- по 2-му способу и 77% -- по 3-му способу; 4-й способ распила применять не следует.

Решение задачи о раскрое

Условие задачи

На швейной фабрике ткань может быть раскроена несколькими способами для изготовления нужных деталей швейных изделий. Пусть при j – м варианте раскроя(j = 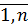) 100 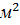ткани изготовляется 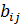деталей i – го вида (I = 1,m), а величина отходов при данном варианте раскроя равна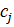 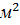. Зная, что деталей i – го вида следует изготовлять 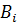штук, требуется раскроить ткань так, чтобы было получено необходимое количество деталей каждого вида при минимальных общих отходах. Составить математическую модель задачи.

Решение.Предположим, что по j-му варианту раскраивается x_j сотен м² ткани. Поскольку при раскрое 100 м² ткани по j-му варианту получается b_ij деталей i-го вида, по всем вариантам раскроя из используемых тканей будет получено

b_i1x₁+b_i2x₂+…+b_inx_n

деталей i-го вида. Так как должно быть изготовлено B_i деталей данного вида, то

b_i1x₁+b_i2x₂+…+b_inx_n=B_i (i = ).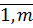

Общая величина отходов по всем вариантам раскроя ткани составит

F=c₁x₁+c₂x₂+…+c_nx_n.

Таким образом, приходим к следующей математической задаче: найти минимум функции

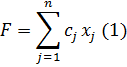
при условии, что ее переменные удовлетворяют системе уравнений

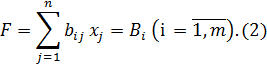
и условию не отрицательности

x_j ≥ 0 .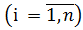

Сформулированная задача является задачей линейного программирования, так как функция (1) линейная, а система (2) содержит только лишь линейные уравнения.

Во всех этих задачах требовалось найти максимум или минимум линейной функции при условии, что ее переменные принимали неотрицательные значения и удовлетворяли некоторой системе линейных уравнений или линейных неравенств либо системе, содержащей как линейные неравенства, так и линейные уравнения. Каждая из этих задач является частным случаем общей задачи линейного программирования.

Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции

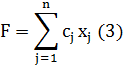
при условиях

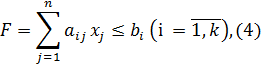
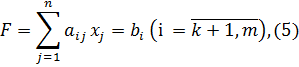
x_j ≥ 0 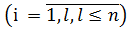,(6)

где 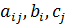- заданные постоянные величины и k ≤ m.

Функция (3) называется целевой функцией (или линейной формой) задачи (3) - (6), а условия (4) - (6) — ограничениями данной задачи.

Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (3) при выполнении условий (4) и (6), где k = m и l=n.

Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (3) при выполнении условий (5) и (6), где k=0 и l=n.

Совокупность чисел X=(x₁, x₂, …, x_n), удовлетворяющих ограничениям задачи (4) - (6), называется допустимым решением (или планом).

План X=(x₁, x₂, …, x_n), при котором целевая функция задачи (3) принимает свое максимальное (минимальное) значение, называется оптимальным.

Значение целевой функции (3) при плане Х будем обозначать через F(X). Следовательно, X^* — оптимальный план задачи, если для любого Х выполняется неравенство F(X)≤F(X^*) (соответственно F(x)≥F(X^*)).

Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.

Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно в общем случае уметь, во-первых, сводить задачу минимизации функции к задаче максимизации, во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот, в-третьих, заменять переменные, которые не подчинены условию не отрицательности.

В том случае, когда требуется найти минимум функции F=c₁x₁+c₂x₂+…+c_nx_n, можно перейти к нахождению максимума функции F₁=- F=-c₁x₁-c₂x₂-…-c_nx_n, поскольку min F=-max(-F).

Ограничение-неравенство исходной задачи линейного программирования, имеющее вид «£», можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида «³» — в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство

a_i1x₁+a_i2x₂+…+a_inx_n≤b_i

преобразуется в ограничение-равенство

a_i1x₁+a_i2x₂+…+a_inx_n+x_n+1=b_i (x_n+1≥0)

а ограничение-неравенство

a_i1x₁+a_i2x₂+…+a_inx_n ≥ b_i

— в ограничение-равенство

a_i1x₁+a_i2x₂+…+a_inx_n-x_n+1=b_i (x_n+1≥0)

В то же время каждое уравнение системы ограничений

a_i1x₁+a_i2x₂+…+a_inx_n = b_i

можно записать в виде неравенств:

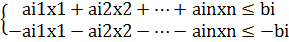
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.

Отметим, наконец, что если переменная x_k, не подчинена условию не отрицательности, то ее следует заменить двумя неотрицательными переменными u_k и v_k, приняв x_k=u_k-v_k.

Заключение

В данной курсовой работе рассмотрели решение задачи о раскрое на примере раскроя тканей.

Решая задачу симплекс-методом, мы нашли необходимое количество деталей каждого вида при минимальных общих отходах и составили математическую модель задачи. Причём полученный результат подразумевает наиболее простые варианты раскроя.

Применение экономико-математических методов в каждом случае внутризаводского планирования должно внедрятся на всех предприятиях страдающих от нехватки ресурсов и не всегда умеющих их экономно расходовать.

Предприятия должны решать многие организационные и технологические проблемы, среди которых одной из важнейших является внедрение современных информационных технологий, решающим образом влияющих на себестоимость и качество выпускаемой продукции. Это позволит не только сократить сроки подготовки программ раскроя, но и существенно снизить расход материала.

Применяя экономико-математические методы на предприятии, а именно методы оптимизации раскроя мы убедились, что данные методы способствуют экономии материала, повышая рейтинг своего предприятия, понижает издержки, что способствует более устойчивому положению на рынке.

Список литературы

1 Алеманов С. А. «Линейное программирование» \\ М., 1981 г.

2 Акулич. И. Л. Математическое программирование в примерах и задачах / И. Л. Акулич. - учеб. пособие для студентов эконом. спец. вузов. – М.: Высшая школа. 1986. –319 с.

3 Лищенко. Линейное и нелинейное программирование / Лищенко. 1987. – 287 с.

4 А.В. Кузнецов «Экономико-математические методы и модели»

5 Холод Н.И. «Математические методы анализа и планирования» \\ М., 1989г.

6 Давыдов Э.Г. «Исследование операций» \\ М., 1990 г.

7 Акоф Р., Самси М. «Основы исследования операций» \\ под ред. Ушакова И.А. – М., 1971 г.