Расчет параметров влажного воздуха
Параметры влажного воздуха рассчитываются по уравнению состояния идеального газа
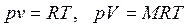 , ,  |
где R = 8314/m, m - мольная масса влажного воздуха.
Подстановка в известное выражение для газовой смеси
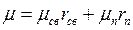  |
значений мольной массы mсв = 29 кг/кмоль, mп = 18 кг/кмоль и объемных долей rп = pп/p, rсв = pсв/p = (p-pп)/p приводит к часто используемым формулам для расчета мольной массы влажного воздуха:
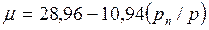  | (7.11) |
или с учетом pп = jps
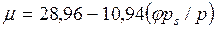 . .  | (7.12) |
Энтальпия влажного воздуха определяется как энтальпия газовой смеси, состоящей из 1 кг сухого воздуха и d кг водяного пара
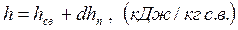 . .  |
Энтальпия 1 кг сухого воздуха равна
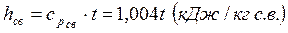 . .  |
Энтальпия 1 кг пара с достаточной точностью вычисляется по формуле
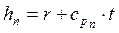 , ,  |
в которой теплота испарения воды при температуре t = 0 0С принята равной 2500 кДж/кг, а теплоемкость пара - равной 1,926 кДж/кг.
Тогда формула для определения энтальпии ненасыщенного влажного воздуха принимает вид
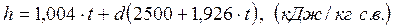 . .  | (7.13) |
Для насыщенного влажного воздуха имеем:
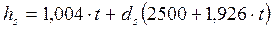 . .  | (7.14) |
7.3. h-d- диаграмма влажного воздуха
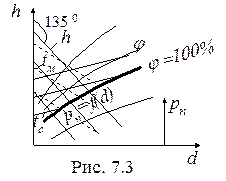 Для определенного атмосферного давления строится h-d- диаграмма. В учебной и технической литературе обычно приводятся или прилагаются диаграммы, построенные для среднего значения атмосферного давления
Для определенного атмосферного давления строится h-d- диаграмма. В учебной и технической литературе обычно приводятся или прилагаются диаграммы, построенные для среднего значения атмосферного давления
p = 745 мм рт. ст. В h-d- диаграмме (рис. 7.3):
1) линии постоянных энтальпий h, кДж/(кг.с.в.) проведены под углом 1350 к вертикали;
2) tc, 0С – изотермы «сухого» термометра;
3) tм, 0С – изотермы «мокрого» термометра;
4) j, % - линии относительных влажностей;
5) pп = f(d)– линия парциальных давлений пара.
Пример пользования диаграммой
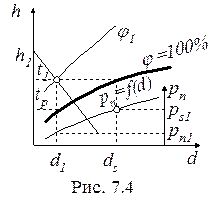 По известным параметрам влажного воздуха t1, j1 найти d1, h1, tp, pп, ps.
По известным параметрам влажного воздуха t1, j1 найти d1, h1, tp, pп, ps.
Изотерма точки росы (tp) проходит (рис. 7.4) через точку пересечения линий d1 = const и
j = 100%.
На оси парциальных давлений (pn) определяются парциальные давления пара (pn) в точке пересечения линий d1 = const и pn = f(d), а также давление насыщения (ps) в точке пересечения линий ds = const и pn = f(d).
Процессы во влажном воздухе
7.4.1.Нагрев воздуха
Влажный воздух с параметрами t1, j1 нагревается при постоянном давлении p = const до температуры t2. Расход воздуха G, кг/с.
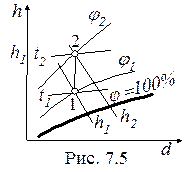 В процессе изобарного нагрева 1-2 (рис.7.5) влагосодержание не изменяется (d = const), относительная влажность уменьшается (j2 < j1), энтальпия увеличивается (h2 > h1).
В процессе изобарного нагрева 1-2 (рис.7.5) влагосодержание не изменяется (d = const), относительная влажность уменьшается (j2 < j1), энтальпия увеличивается (h2 > h1).
Теплота, необходимая для нагрева 1 кг сухого воздуха, равна
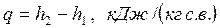 . .  | (7.15) |
Учитывая, что расход влажного воздуха
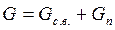 , ,  |
отсюда
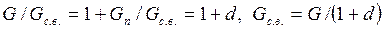 . .  | (7.16) |
Соответственно секундный расход тепла имеет вид
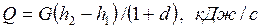 . .  | (7.17) |
Охлаждение воздуха
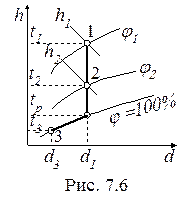 Влажный воздух с параметрами t1, j1 охлаждается при постоянном давлении p = const до температуры t2 (t3) Расход воздуха G.
Влажный воздух с параметрами t1, j1 охлаждается при постоянном давлении p = const до температуры t2 (t3) Расход воздуха G.
Различают два случая:
1) t2 > tp (процесс 1-2, рис. 7.6). В этом случае:
· влагосодержание не изменяется (d = const);
· относительная влажность увеличивается
(j2 > j1);
· энтальпия уменьшается (h2 <h1).
Теплота, отводимая от воздуха,
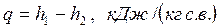 , ,  | (7.18) |
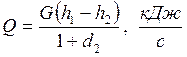 . .  | (7.19) |
2) Если температура, до которой охлаждается воздух (t3), меньше температуры точки росы (процесс 1-3), то воздух, достигнув состояния насыщения (t = tp, j = 100%), при дальнейшем понижении температуры будет оставаться насыщенным и из него будет выпадать влага, поскольку d3 < d1.
Теплота, отводимая от воздуха в этом случае,
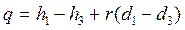 , , 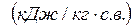 , ,  | (7.20) |
где r = 2500 кДж/кг;
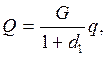 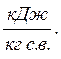  | (7.21) |
В практике охлаждение воздуха до t < tp широко применяют с целью удаления из него влаги (осушения).
Сушка материалов
В процессе сушки различных материалов воздух является сушильным агентом, и чем выше его температура, а, следовательно, давление насыщения (ps), тем больше он может поглотить влаги.
Пусть параметры воздуха на входе в сушильную камеру равны t1 , j1, расход воздуха - G.
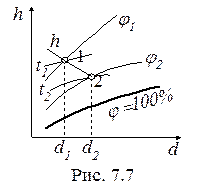 Идеальный процесс сушки (без потерь тепла в окружающую среду) - это процесс 1-2 при постоянной энтальпии (рис. 7.7). В процессе сушки:
Идеальный процесс сушки (без потерь тепла в окружающую среду) - это процесс 1-2 при постоянной энтальпии (рис. 7.7). В процессе сушки:
· относительная влажность воздуха увеличивается (j2 > j1);
· температура уменьшается (t2 < t1);
· влагосодержание увеличивается (d2 > d1).
Количество влаги, воспринятой воздухом, вычисляется по формулам:
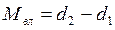 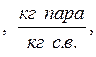  | (7.22) |
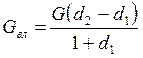 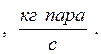  | (7.23) |
В реальных процессах сушки h2 < h1 из-за потерь тепла в окружающую среду.
