Зависимость параметров жидкости, газа и пористой среды от давления

Выведенные дифференциальные уравнения (1.2, 1.4) содержат параметры, которые характеризуют жидкость или газ: плотность r, вязкость m, а также параметры пористой среды – коэффициенты пористости m и проницаемости k. Для дальнейших расчетов надо знать зависимость этих коэффициентов от давления.

Плотность капельной жидкости. При установившейся фильтрации капельной жидкости можно считать ее плотность, не зависящей от давления, то есть рассматривать жидкость как несжимаемую: r = const.

В неустановившихся процессах необходимо учитывать сжимаемости жидкости, которая характеризуется коэффициентом объемного сжатия жидкости b_ж. Этот коэффициент обычно считают постоянным:

,

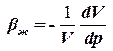(1.44)

где V – объем жидкости.

Для нефтей различных месторождений коэффициенты объемного сжатия составляют (7 – 30) 10^-10 Па^-1, для пластовых вод (2,7 – 5) 10^-10Па^-1.

В последней формуле перейдем от объемов к плотности и получим:

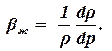(1.45)

Проинтегрировав последнее равенство от начального значений давления р₀ и плотности r₀ до текущих значений, получим:

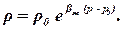(1.46)

При перепадах давлений до 20 МПа показатель степени b_ж (р ‑ р₀) ≈ 0,01 << 1. В этом случае можно, разложив экспоненту в ряд Тейлора, ограничиться двумя первыми членами ряда:

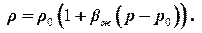(1.47)

При этом получаем линейную зависимость плотности от давления.

Плотность газов. Сжимаемые жидкости (газы) при малых изменениях давления и температуры также можно характеризовать коэффициентами объёмного сжатия и температурного расширения. Но при больших изменениях давлений и температур эти коэффициенты меняются в больших пределах, поэтому зависимость плотности идеального газа с давлением и температурой находятся на основе уравнения состояния Клайперона – Менделеева:

,

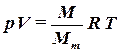(1.48)

где p – абсолютное давление, Па;

V – объём, который занимает газ, м³;

M – масса газа, кг;

M_m – молекулярная масса газа, кг/кмоль;

R = 8,314 Дж/моль·– универсальная газовая постоянная, не зависящая от состава газа;

T= 273,14 + t – абсолютная температура, K.

Разделим последнее уравнение на объём получим:

,

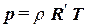(1.49)

где R’ = R/M_m – газовая постоянная, зависящая от состава газа.

Газовая постоянная для воздуха и метана соответственно равны , R΄_{воздуха} = 287 Дж/кг K˚; R΄_метан = 520 Дж/кг K˚.

Последнее уравнение иногда записывают в виде:

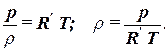(1.50)

Из последнего уравнения видно, что плотность газа зависит от давления и температуры, поэтому если известна плотность газа, то необходимо указывать давление, температуру и состав газа, что неудобно. Поэтому вводятся понятия нормальных и стандартных физических условий.

Нормальные условия соответствуют температуре t = 0°С и давлению p_ат = 0,1013°МПа. Плотность воздуха при нормальных условиях равна ρ_в.н.ус = 1,29 кг/м³.

Стандартные условия соответствуют температуре t = 20°С и давлению p_ат = 0,1013°МПа. Плотность воздуха при стандартных условиях равна ρ_в.ст.ус = 1,22 кг/м³.

Поэтому по известной плотности при данных условиях можно рассчитать плотность газа при других значениях давления и температуры:

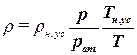(1.51)

или

.

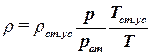(1.52)

Обычно температура пласта T_пл постоянна, поэтому при давлении p_ат = 0,1013 МПа и пластовой температуре плотность газа r_ат будет равна:

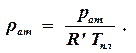(1.53)

Исключая пластовую температуру, получим уравнение состояния идеального газа, которым будем пользоваться в дальнейшем:

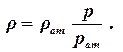(1.54)

Природные газы можно считать идеальными (совершенными), если пластовые давления газовых месторождений невелики (до 6 – 9 МПа) и газ отбирается при депрессии до 1 МПа. В настоящее время в практике все чаще встречаются газовые месторождения с высокими пластовыми давлениями (до 40 – 60 МПа), которые иногда эксплуатируются с большими депрессиями (порядка 15 – 30 МПа). В этих условиях следует использовать уравнение состояния реального газа

,

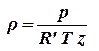(1.55)

где z – коэффициент, характеризующий степень отклонения состояния реального газа от закона идеальных газов (коэффициент сверхсжимаемости) и зависящий для данного газа от давления и температуры z = z(p, Т). Значения коэффициента сверхсжимаемости z определяются по графикам Д. Брауна.

Вязкость нефти. Эксперименты показывают, что коэффициенты вязкости нефти (при давлениях выше давления насыщения) и газа увеличиваются с повышением давления. При значительных изменениях давления (до 100 МПа) зависимость вязкости пластовых нефтей и природных газов от давления можно принять экспоненциальной:

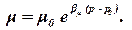(1.56)

При малых изменениях давления эта зависимость имеет линейный характер.

Здесь m₀ – вязкость при фиксированном давлении p₀; β_m – коэффициент, определяемый экспериментально и зависящий от состава нефти или газа.

Пористость пласта. Чтобы выяснить, как зависит от давления коэффициент пористости, рассмотрим вопрос о напряжениях, действующих в пористой среде, заполненной жидкостью. При уменьшении давления в жидкости увеличивается силы на скелет пористой среды, поэтому пористость уменьшается.

Вследствие малой деформации твердой фазы считают обычно, что изменение пористости зависит от изменения давления линейно. Закон сжимаемости породы записывают следующим образом, вводя коэффициент объемной упругости пласта b_с:

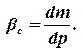(1.57)

Интегрируя полученное выражение, получим:

m = m0 + bс (p – p0),

(1.58)

где m₀ – коэффициент пористости при давлении p₀.

Лабораторные эксперименты для разных зернистых пород и промысловые исследования показывают, что коэффициент объемной упругости пласта составляет (0,3 – 2) 10^-10 Па^-1.

При значительных изменениях давления изменение пористости описывается уравнением:

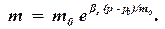(1.59)

Проницаемость пласта. Экспериментально показано, что не только пористость, но и проницаемость существенно изменяются с изменением пластового давления, причем часто проницаемость значительнее, чем пористость. При малых изменениях давления эту зависимость можно принять линейной:

k = k0 (1 + bk (p – p0)),

(1.60)

а при больших – экспоненциальной:

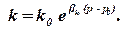(1.61)

В трещиноватых пластах проницаемость изменяется в зависимости от давления более интенсивно, чем в пористых, поэтому в трещиноватых пластах учет зависимости k(p) более необходим, чем в гранулярных.

Уравнения состояния жидкости или газа, насыщающих пласт, и пористой среды замыкают систему дифференциальных уравнений.