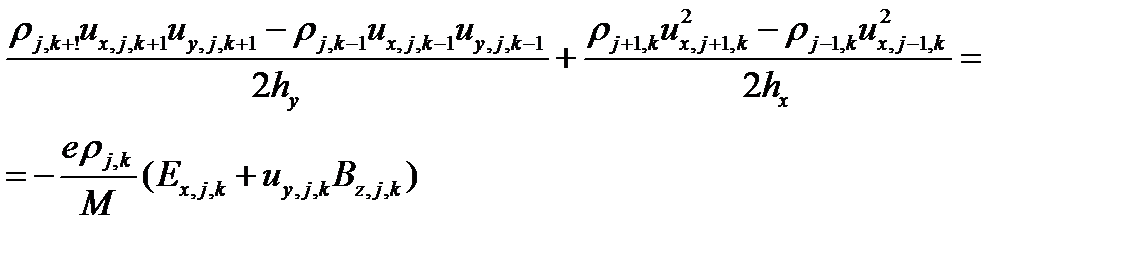Метод конечных объемов
Ранее поминался метод подобластей, послуживший отправной точкой для ряда численных методов. Одним из таких методов является метод конечных объемов. Этот же метод является представителем еще одного широко распространившегося класса – интегральных методов. От классической формы записи метода подобластей взято разбиение расчетной области на подобласти и интегрирование невязки по подобласти. Отличием является отсутствие явной записи аппроксимирующей (пробной) функции. Но, по-прежнему, пытаемся «точно» решить уравнение в каждой подобласти. Поэтому по подобласти интегрируется исходное уравнение. Интегральные методы характеризуются тем, что сначала берется интеграл от дифференциального уравнения, получается интегральная форма записи уравнения. Затем уравнение в этой форме применяют к отдельным ячейкам сетки. В данном случае ячейки и подобласти – это одно и то же.
На самом деле, интегральная форма записи уравнений имеет (с точки зрения физики) даже более широкую область применения, чем дифференциальная. Дело в том, что при наличии разрывов функции, дифференциальные уравнения неприменимы, а их интегральные аналоги продолжают работать, работать и работать…. К сожалению, при их численной реализации это преимущество иногда утрачивается.
Как правило, интегралы от уравнений имеют простой и понятный физический смысл. Для примера рассмотрим уравнение неразрывности. Исходное дифференциальное уравнение записывается
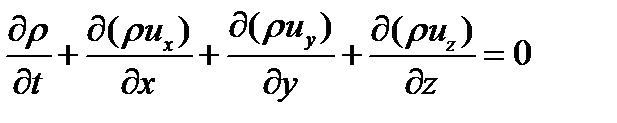
проинтегрируем его по объему V, имеющему поверхность S, и по времени в интервале от t0 до t1. При интегрировании производных воспользуемся формулой Стокса (частные случаи ее носят названия формул Грина и Остроградского-Гаусса). В результате получаем
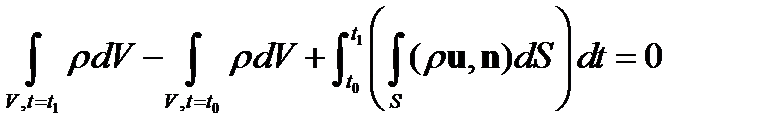
В этой записи разность между первыми двумя интегралами означает изменение массы в заданном объеме за рассматриваемый интервал времени. А двойной интеграл показывает массу, втекающую в данный объем через ограничивающую его поверхность за тот же промежуток времени. Естественно, раз речь идет о численных методах, то эти интегралы считаются приближенно. И здесь начинаются вопросы аппроксимации, аналогичные тем, что рассматривались в методе конечных разностей.
Рассмотрим один из простейших случаев – двумерная прямоугольная равномерная сетка. В методе конечных объемов обычно значения функций определяются не в узлах сетки, а в центрах ячеек. Индексируются, соответственно, тоже не линии сетки в каждом направлении, а слои ячеек[9] (см. рис.).
| j-1 |
| j |
| j+1 |
| k-1 |
| k |
| k+1 |
| A |
| B |
| C |
| D |
Для данного случая интегральная форма уравнения запишется так
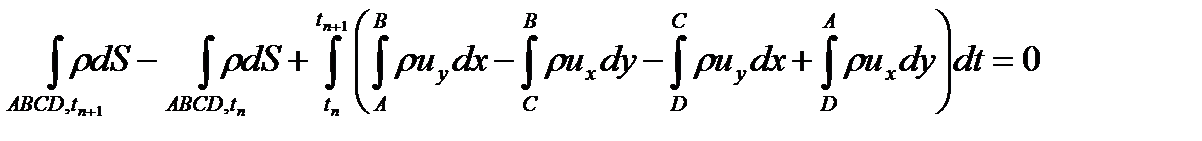
Простейшая аппроксимация такого уравнения запишется так
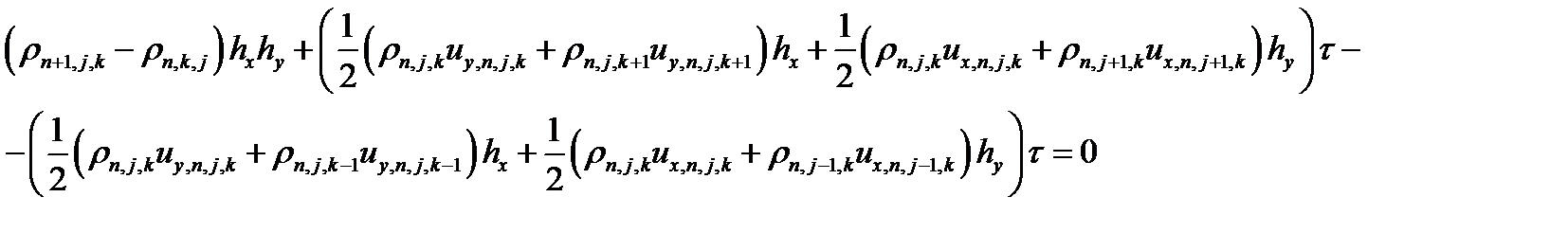после сокращений получаем формулу
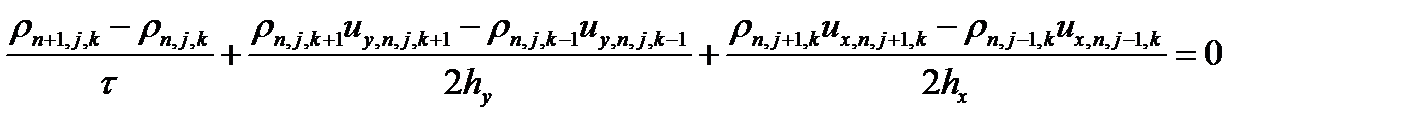
Как видим, в данном случае мы получили обычное уравнение, какое могли написать и с помощью метода конечных разностей. Значит, к нему можно применять и те же методы исследования устойчивости. (Вопрос «на засыпку»: а устойчива ли данная схема?)
Но если мы получили то же самое, то стоило ли городить весь этот огород? В простейших случаях действительно никаких преимуществ мы не получаем. Но в ситуациях посложнее преимущества проявляются. Во-первых, как отмечалось выше, такие методы (даже в такой простейшей реализации) гораздо лучше описывают разрывы и области с высокими градиентами. При этом гарантируется выполнение законов сохранения массы, импульса и энергии, так как они соблюдаются в каждой ячейке. Во-вторых, эти методы выдерживают самые разнообразные издевательства над сеткой. Даже криволинейные, неравномерные и нерегулярные сетки не выбивают эти методы из колеи. Особенно часто эти преимущества ощущаются при задании граничных условий.
| j-1 |
| j |
| j+1 |
| k-1 |
| k |
| k+1 |
| A |
| B |
| C |
| D |
| E |
Например, для случая показанного на рисунке интегральная форма уравнения будет иметь вид
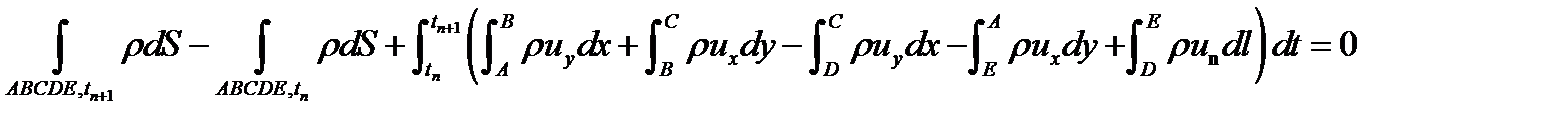
то есть просто там, где интеграл брали по площади полной ячейки, теперь берем по площади «обрезанной», там, где брали интеграл по полному ребру, теперь берем по оставшейся его части. Добавился интеграл по участку границы. Но он легко находится из граничных условий. В частности, если через стенку не подается массовый расход (а также не уносится масса с поверхности и/или пренебрегаем массовым потоком ионов, теряющих заряд на стенке), то такой интеграл просто равен нулю. В аналогичной записи уравнения энергии поток через стенку, как правило, приходится учитывать. Но его тоже нетрудно найти из граничных условий (если они правильно поставлены).
Для закрепления распишем, как будет выглядеть применение метода конечных объемов к одному из уравнений сохранения импульса. Возьмем плоский стационарный случай для однозарядных ионов. Пренебрежем вязкостью и упругими столкновениями. Получаем уравнение
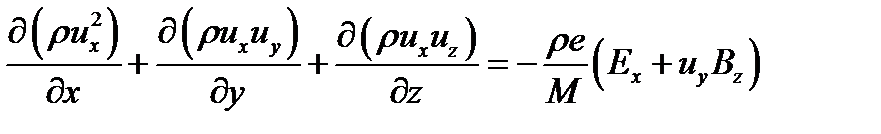
Для прямоугольной сетки (см рис. выше) получаем
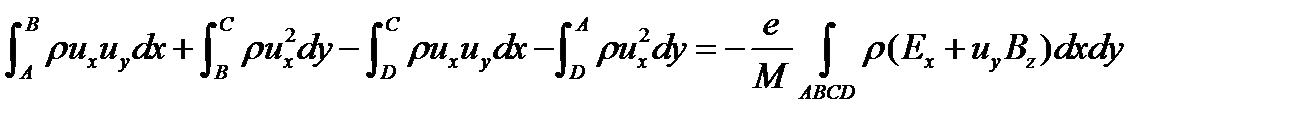
Простейшая аппроксимация такого уравнения запишется так
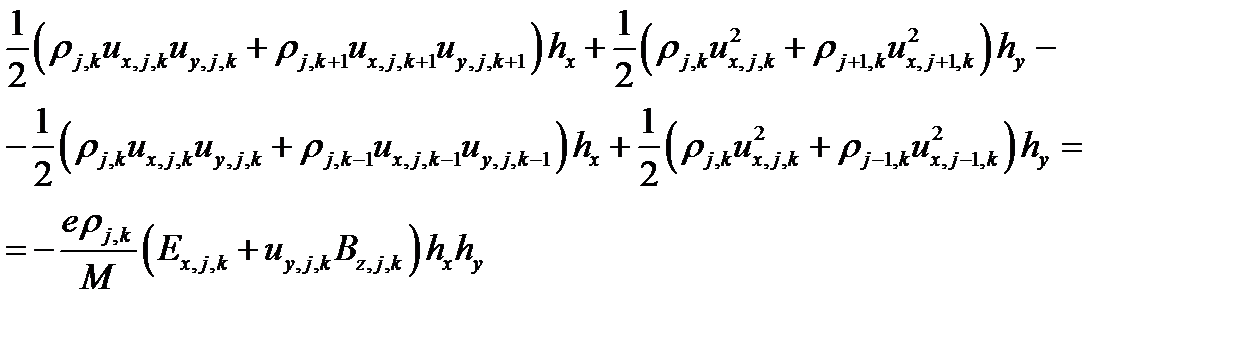
после сокращений получаем формулу
