Определение концентрации раствора сахара с помощью сахариметра
Целью настоящей работы является изучение явления поляризации, исследование явления вращения плоскости поляризации, определение концентрации раствора сахара, проверка законов Малюса и Брюстера.
Приборы и принадлежности: сахариметр СУ-2, трубки с раствором сахара, газовый гелий-неоновый лазер, диэлектрическая пластинка.
3.1. Теоретическое введение
С точки зрения электромагнитной теории свет представляет собой поперечную электромагнитную волну, в которой колебания векторов напряженности электрического и магнитного полей происходят перпендикулярно направлению распространения света (рис.3.1).
Вектор напряженности электрического поля волны Е часто называют 2 световым вектором. Это обусловлено тем, что физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями электрического вектора.
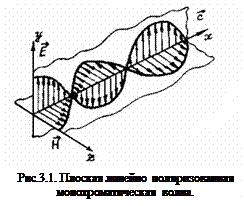 Е и Н - вектора напряженности - соответственно электрического и магнитного полей; С - вектор скорости распространения волны.
Е и Н - вектора напряженности - соответственно электрического и магнитного полей; С - вектор скорости распространения волны.
Излучение светящегося тела слагается из волн, испускаемых отдельными атомами тела. Излучение отдельного атома продолжается 10-8с. От каждого атома (атомы ориентированы хаотично) распространяются колебания Е и Н, происходящие в определенной плоскости (рис.3.1). Мы же наблюдаем всегда суммарное действие многих атомов, а именно: множество всех возможных ориентировок Е и Н и быструю смену этих возможных ориентировок.
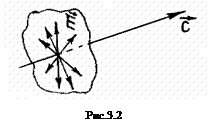 Таким образом, свет, испускаемый обычными источниками, не имеет пре имущественного направления колебаний, в нем представлены все направления колебаний Е, перпендикулярные к лучу. На рис.3.2 показаны некоторые из возможных колебаний вектора. Е (вектор Н не указан).
Таким образом, свет, испускаемый обычными источниками, не имеет пре имущественного направления колебаний, в нем представлены все направления колебаний Е, перпендикулярные к лучу. На рис.3.2 показаны некоторые из возможных колебаний вектора. Е (вектор Н не указан).
Свет со всеми возможными ориентировками вектора Е (а, следовательно, и вектора Н) называется естественным. В естественном свете колебания различных направлений представлены с равной вероятностью (рис.3.2).
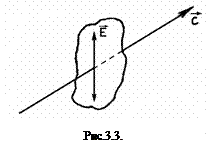
Свет, в котором Е (а, следовательно, и Н) имеет одно единственное направление, называется плоскополяризованным (см. рис.3.1).
 Плоскость, проходящая через направление колебаний светового вектора Е и направление распространения волны, называется плоскостью поляризации.
Плоскость, проходящая через направление колебаний светового вектора Е и направление распространения волны, называется плоскостью поляризации.
На рис.3.3 показано направление колебания вектора Е в плоскополяризованном свете. Из сказанного следует, что естественные источники света излучают волны не поляризованные. Плоскополяризованный свет можно получить из естественного с помощью приборов, называемых поляризаторами (призма Николя, поляроид и т.д.).
Эти приборы способны свободно пропускать световые волны, электрический вектор напряженности которых колеблется лишь в строго определенном направлении. Это направление называется главным направлением. На рис.3.4 РР - главное направление поляризатора.
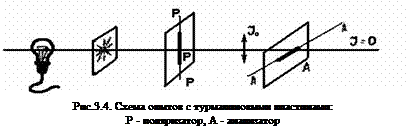
Для того чтобы установить направление колебаний поляризованного света, на его пути ставят анализатор, который по своему устройству не отличается от поляризатора. Анализатор, как и поляризатор, может пропускать только те колебания, которые совпадают с его главным направлением АА (рис 3.4.) если же анализатор повернуть так, что его главное направление АА составит угол 900 с главным направлением поляризатора РР, то за анализатором будет темнота, интенсивность проходящего света будет равна нулю (рис. 3.4.). Такое положение анализатора называется скрещенным. В том случае, когда главные направления поляризатора и анализатора, которые составляют между собой угол φ, интенсивность проходящего света будет принимать промежуточные значения. Зависимость между интенсивностью J и углом φ можно понять из векторной диаграммы (рис. 3.5.).
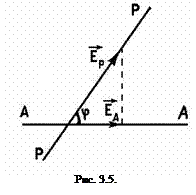 Пусть РР и АА соответственно главные направления поляризатора и анализатора, которые составляют между собой угол φ.
Пусть РР и АА соответственно главные направления поляризатора и анализатора, которые составляют между собой угол φ.
ЕР - амплитуда светового вектора ĒР., пропускаемого поляризатором;
ЕA - амплитуда светового вектора ĒА, выходящего из анализатора.
Как видно из рис. 3.5, ЕА равна проекции ЕР на главное направление анализатора АА, т.е. ЕА = ЕР•cos φ.
Так как известно, что интенсивность света пропорциональна квадрату амплитуды J ~ Е2, то J = J0 cos2φ (закон Малюса), где J0 - интенсивность света, падающего на анализатор, J - интенсивность света, прошедшего через анализатор.
Если cos φ =1, то J= J0, т.е. J0 есть интенсивность поляризованного света в случае совпадения главных направлений поляризатора и анализатора.
При прохождении плоскополяризованного света через некоторые вещества наблюдается вращение его плоскости поляризации. Вещества, обладающие такой способностью, называются оптически активными. К ним относятся: кристаллические тела (например, кварц, киноварь), чистые жидкости (скипидар, никотин) и растворы оптически активных веществ (водные растворы сахара, винной кислоты и др.). Направление вращения различных веществ различно: правовращающие и левовращающие. Правовращающим называется тело, в котором плоскость колебаний для наблюдателя, смотрящего навстречу световому лучу, поворачивается по часовой стрелке. Левовращающие тела вращают плоскость колебаний того же луча против часовой стрелки.
Если между скрещенными поляризатором и анализатором, дающими темное поле зрения, поместить оптически активное вещество, то поле зрения просветлеет. Однако если повернуть анализатор на некоторый угол φ, то можно вновь получить темное поле зрения.
В растворах угол поворота плоскости поляризации пропорционален длине пути луча в растворе l и концентрации активного вещества С.
φ=[α]•С•l, (3.1)
где [α] - величина, называемая удельной постоянной вращения данного вещества. Она численно равна углу поворота плоскости поляризации в слое раствора 1 дм при концентрации 100 г вещества в 100 см3 раствора при температуре 200С. Она также зависит от длины волны проходящего света. Поэтому формула справедлива только в случае монохроматического света, для получения которого используются светофильтры. Например, для желтой линии натрия удельная постоянная вращения раствора сахара при нормальной температуре равна:
[α] = 52,6 град•дм-1г-1•см 3.
3.2. Описание универсального сахариметра
Универсальный сахариметр, как всякий поляризационный прибор, состоит из двух основных частей: поляризатора и анализатора, представляющих собой призмы Николя (рис.3.6).
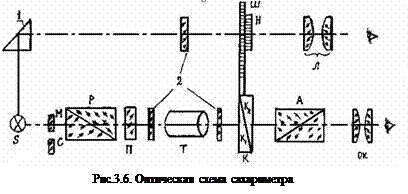
Пучок лучей от источника света S проходит через матовое стекло М, предназначенное для рассеивания света. Вместо матового стекла М в оптическую систему может быть введен светофильтр С. Далее световой пучок попадает в поляризатор P и выходит из него плоскополяризованным. После поляризатора свет проходит через полутеневую пластинку П из кварца-стекла, камеру для поляриметрических трубок с растворами сахара Т, кварцевый компенсатор K, анализатор А.
Прибор, как видно из схемы сахариметра, имеет полутеневую пластинку П, которая состоит из двух половинок: стеклянной C и кварцевой K (рис.3.7); АВ - граница раздела стекла и кварца.
Допустим, что на пластинку падает монохроматический свет линейно поляризованный, с плоскостью колебаний РР. Через стеклянную пластинку свет пройдет, не изменив плоскости колебаний, а через кварцевую пластинку выйдет свет с новой плоскостью колебаний Р1Р1, т. к. кварц - оптически активное вещество (рис.3.7). Если затем пропустить оба луча через анализатор, у которого плоскость колебаний, например,
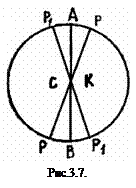 перпендикулярна PP, то луч левой половины поля зрения "С" будет погашен, и поле зрения в этой половине будет темным, тогда как часть света правой половины будет пропущена анализатором, и поле этой половины будет светлым. Если плоскость колебаний анализатора перпендикулярна P1Р1, то будет обратное явление. Можно найти среднее положение анализатора, при котором обе половины поля зрения в полутеневом сахариметре будут
перпендикулярна PP, то луч левой половины поля зрения "С" будет погашен, и поле зрения в этой половине будет темным, тогда как часть света правой половины будет пропущена анализатором, и поле этой половины будет светлым. Если плоскость колебаний анализатора перпендикулярна P1Р1, то будет обратное явление. Можно найти среднее положение анализатора, при котором обе половины поля зрения в полутеневом сахариметре будут
одинаково освещены - "нулевая точка". Исследуемая жидкость - раствор сахара - помещается между полутеневой пластинкой из кварца-стекла и анализатором, предварительно установленным на нулевую точку. Угол, на который надо повернуть анализатор, чтобы достигнуть равной освещенности, очевидно, равен углу поворота плоскости колебаний.
Кварцевый компенсатор
Чтобы пользоваться полутеневым сахариметром, вводят приспособление, позволяющее применять белый свет - кварцевый компенсатор. Кварцевый компенсатор K (рис.3.6) состоит из двух клиньев с острыми углами. Клинья сделаны из левовращающего кварца (вращает плоскость поляризации против часовой стрелки). На рис.3.6 К1 - неподвижный клин, К2 - подвижный клин. Перемещая К2 относительно К1, можно изменить величину левого вращения плоскости поляризации, даваемого клиньями К1 и К2. Так как раствор сахара вращает плоскость поляризации вправо (по часовой стрелке), то вращение, полученное от раствора сахара, можно компенсировать левым вращением кварцевого компенсатора при определенной толщине обоих клиньев. При этом компенсация происходит одновременно для всех длин волн, и прибор может освещаться белым светом, т.к. зависимость удельного вращения от длины волны у кварца и сахарных растворов приблизительно одинакова. Описанный сахариметр компенсирует только одно правое вращение, т.е. не пригоден для исследования левовращающих растворов.
Свет от электролампочки S служит также для освещения шкалы Ш и нониуса Н, что достигается при помощи отражательной призмы 1 и защитного стекла 2, рассеивающего свет. Цифры и деления нониуса Н и шкалы Ш рассматриваются в увеличенном виде при помощи лупы Л, состоящей из двух линз. Шкала Ш связана с подвижным кварцевым клином K2. Таким образом, смещение подвижного кварцевого клина K2, пропорциональное углу вращения плоскости поляризации, вызванного исследуемым раствором, передается на шкалу Ш и отсчитывается при помощи лупы Л.
В сахариметре применена международная сахарная шкала. 1000 этой шкалы соответствуют 34,620 угловым. На рис.3.8 показан внешний вид сахариметра.
Основными частями прибора являются узел измерительной головки 2 и осветительный узел 7, соединенные между собой траверсой 5, на которой укреплена камера 4 для поляриметрических трубок.
С лицевой стороны головки прибора имеется лупа в оправе 1 для отсчета показаний по шкале и зрительная труба 13 поля зрения. С тыльной стороны измерительной головки находится узел нониуса 3 . В нижней части измерительной головки расположена рукоятка 12 для перемещения подвижного кварцевого клина и связанной с ним шкалы.
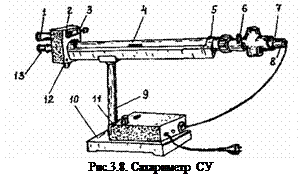 Осветительный узел имеет передвигающуюся рамку 6, в которой находится стеклянный светофильтр и матовое стекло, патрон с лампочкой 8. Электролампочка подключается через понижающий трансформатор 11 в сеть переменного тока 220в. Прибор установлен на колонке 9, укрепленной в чугунном основании 10.
Осветительный узел имеет передвигающуюся рамку 6, в которой находится стеклянный светофильтр и матовое стекло, патрон с лампочкой 8. Электролампочка подключается через понижающий трансформатор 11 в сеть переменного тока 220в. Прибор установлен на колонке 9, укрепленной в чугунном основании 10.
3.3. Выполнение работы
Упражнение 1. Определение концентрации раствора сахара.
1. Включить прибор в сеть. После включения тумблера на корпусе трансформатора должна загореться лампочка (рис.3.8).
2. Ввести оранжевый светофильтр с помощью рамки 6.
3. Окуляр зрительной трубы 13 поля зрения и отсчетную лупу 1 шкалы необходимо установить по глазу наблюдателя. Для этого вращением оправ их передвигают вдоль оси, чтобы в поле зрения окуляра зрительной трубы 13 вертикальная линия, разделяющая поле зрения на две половины, была четко и ясно видна, а в поле зрения отсчетной лупы 1 четко и ясно были видны цифры и штрихи шкалы и нониуса. Это делается при отсутствии в камере поляриметрической трубки.
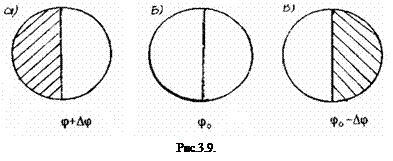
4. Произвести "нулевую установку" прибора (нуль прибора), т.е. определить φ0 прибора. Для этого, при отсутствии в камере прибора поляриметрической трубки, вращая рукоятку 12, добиться полной однородности обеих половинок поля зрения (см. рис.3.9б). При малейшем повороте рукоятки 12 в ту или иную сторону (φ0+Δφ, φ0-Δφ) освещенности половинок поля зрения будут меняться: то одна половина будет темной, то другая, так, как показано на рис.3.9а и 3.9в.
Если в момент полной однородности (рис.3.9б) поля зрения нулевые деления шкалы и нониуса совпадают, то φ0 =0. Если же нулевые деления не совпадают при равенстве освещенности, то берут отсчет и записывают φ0. Таким образом, отсчет φ0 берется всегда в момент равенства освещенности обеих половинок поля зрения.

Отсчет φ0 повторить три раза, всякий раз нарушая равенство освещенности обеих половинок поля зрения с помощью рукоятки 12 (рис.3.8).
Определить среднее арифметическое из числа n измерений φ0 ср. Значение φ0 будет давать нулевое положение прибора, нуль прибора. Измерения занести в табл.3.1.
5. Взять поляриметрическую трубку и налить в нее известный раствор N1. Трубку завинтить и вложить в камеру прибора.
Если теперь посмотреть в окуляр зрительной трубы 13 (рис.3.8), то увидим, что однородность поля зрения нарушилась, т.е. одна половина поля зрения стала темной, а другая светлой. Вновь добиться одинаковой минимальной освещенности поля зрения, как это делалось в п.4.
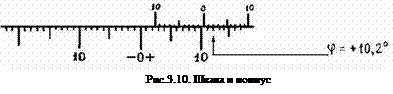
По шкале определить угол φ1 с точностью до 0,10. Измерения φ1 повторить три раза для одного и того же раствора и вычислить φ1 ср. Отсчеты φ0 могут быть как положительными, так и отрицательными. Отсчет берется со знаком минус, когда нуль нониуса расположен левее нуля шкалы. При этом десятые доли градуса берутся в левой части нониуса, там, где деление нониуса, точнее, лучше всего совмещается с одним из делений шкалы. Положительный отсчет - когда нуль нониуса правее нуля шкалы (рис.3.10).

6. Измерения и вычисления занести в табл. 3.1. Угол поворота плоскости поляризации α1 в делениях шкалы найти как разность:
α1= φ1 ср - φ0 ср
7. Раствор N1 из трубки вылить в ту же колбу N1.
8. То же самое (пункты 5,6,7) повторить с другими эталонными растворами.
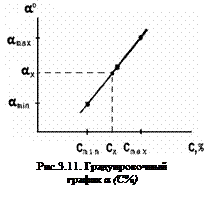
9. По полученным данным (табл.3.1) построить градуировочную кривую сахариметра, т.е. график зависимости угла поворота плоскости поляризации α в делениях шкалы от концентрации сахара в растворе С. Для этого по оси Х отложить значения концентрации сахара в процентах, по оси Y - значения угла поворота в градусах (рис.3.11).
 По градуировочной кривой можно сказать, что данный угол поворота плоскости поляризации соответствует такой-то концентрации раствора. В этом и заключается смысл градуировки сахариметра.
По градуировочной кривой можно сказать, что данный угол поворота плоскости поляризации соответствует такой-то концентрации раствора. В этом и заключается смысл градуировки сахариметра.
10. Определить неизвестную концентрацию раствора сахара. Для этого в поляриметрическую трубку налить раствор неизвестной концентрации и определить угол поворота плоскости поляризации данным раствором φx, аналогично тому, как это делалось в пунктах 5,6,7, вычислить φx ср. и найти αx 0= φx ср. - φ0 ср.
Пользуясь градуировочным графиком (рис.3.11) по значению αx определить значение неизвестной концентрации. Для этого по оси Y отложить значение αx и провести прямую до пересечения с кривой, опустить перпендикуляр на ось Х и взять значение Cx там, где этот перпендикуляр пересекает ось концентраций. Масштаб выбирают такой, чтобы удобно укладывались на осях рабочие области (рабочие интервалы ΔC и Δα).
11. Результаты измерений занести в табл.3.1.
Таблица 3.1
| φ0, град | φ0 ср,,град | С, % | φ, град | φср, град | α |
| 1. 2. 3. | С1 | 1. 2. 3. | |||
| С2 | 1. 2. 3. | ||||
Примечания:
1. Покровное стекло у трубки не следует прижимать очень сильно, так как при этом оно может стать оптически активным, т.е. вызвать дополнительное вращение плоскости поляризации.
2. Наливать раствор в трубку следует медленно, чтобы избежать образования воздушных пузырьков, которые затрудняют проведение измерений.
Упражнение 2. Проверка закона Малюса. Определение коэффициента
преломления вещества с помощью закона Брюстера
Практическая часть
Все детали установки располагаются на оптической скамье. В качестве источника излучения используется газовый гелий-неоновый лазер, имеющий линейно-поляризованное излучение.
При изучении закона Малюса используется еще поляризатор, выполняющий роль анализатора, так как излучение лазера линейно поляризовано, а также измеритель относительной интенсивности лазерного излучения. Для изучения закона Брюстера используется тот факт, что при падении света на диэлектрическую пластинку под углом Брюстера, составляющая электрического поля Е, параллельная плоскости падения, не отражается. Поэтому, если сориентировать плоскость поляризации лазерного излучения параллельно плоскости падения излучения на излучаемый образец, то при угле падения, равном φБр=arctg n, где n - коэффициент преломления диэлектрика, отраженного луча быть не должно. Реально же, интенсивность отраженного луча проходит через минимум при плавном изменении угла падения, что легко обнаруживается визуально. Установка в этом случае состоит из лазера, сориентированного соответствующим образом, и столика, на котором крепится исследуемый образец.
Порядок выполнения упражнения
I. Закон Малюса
1. Установить на оптической скамье кроме лазера поляризатор-анализатор и фотодатчик измерителя относительной интенсивности лазерного излучения.
2. Лаборант включает лазер. Добиться нормального расположения плоскости анализатора к лучу лазера и четкого попадания прошедшего луча на фотодатчик.
3. Включить измеритель относительной интенсивности лазерного излучения. Вращая анализатор, добиться максимальных показаний прибора. Этим мы достигнем параллельности осей поляризации лазерного излучения и анализатора.
4. Снять зависимость J интенсивности прошедшего лазерного излучения от угла α между осями поляризации лазерного излучения и анализатора. Построить график J= f(α).
II. Закон Брюстера.
1. Установить на оптической скамье столик с образцом.
2. Лаборант включает лазер. Добиться перпендикулярного положения плоскости диэлектрической пластинки к лазерному излучению. Плоскость поляризации лазерного излучения должна быть сориентирована параллельно плоскости падения на образец. Для более четкой ориентации плоскости поляризации можно воспользоваться анализатором.
3. Отметив первоначальное положение стрелки-указателя держателя образца относительно лимба, плавно повернуть держатель с образцом вокруг вертикальной оси до получения минимальной интенсивности отраженного луча, наблюдаемого на экране. По достижении минимальной интенсивности вновь отметить положение стрелки относительно лимба. Разность показаний и дает величину Брюстера для данного образца.
4. Повторить те же операции для других образцов.
5. Заполнить таблицу.
| № образца | φБр | n = tg φБр |
3.4. Контрольные вопросы
1. Свет как электромагнитные волны. Поперечность световых волн.
2. Что такое интенсивность света?
3. Какой свет называется плоскополяризованным?
4. Какая плоскость называется плоскостью поляризации?
5. Чем отличается естественный свет от поляризованного? Почему обычные источники дают не поляризованный свет?
6. Как можно получить поляризованный свет? Что такое поляризатор?
7. В чем заключается явление вращения плоскости поляризации? Какие вещества называются оптически активными? Привести примеры таких веществ.
8. Объясните закон Малюса. Что такое анализатор?
9. От чего зависит угол поворота плоскости поляризации? Что называется удельным вращением вещества? От чего оно зависит?
10. Каково назначение сахариметра?
11. Каким образом происходит выравнивание освещенностей обеих половинок поля зрения? Объясните на рисунках.
12. Объясните закон Брюстера.
Литература
[1], §§ 134, 135, 136, 141;
[2], 7 §§ 0 34.1, 34.2, 34.5;
[3], §§ 191-194, 196;
[4], ч. II, гл. VII, §§ 58-60;
[5], §§ 5-7, 101-106, 108, 163-167;
[6], стр. 274-283.
СПИСОК ЛИТЕРАТУРЫ
1. Савельев И.В. Курс общей физики: Учебное пособие. В 3-х т. Т.2. Электричество и магнетизм. Волны. Оптика. 3-е изд., испр.- М.: Наука, 1988. - 496 с., ил.
2. Детлаф А.А., Яворский Б.М. Курс физики. - М.: Высш. шк., 1989. - 608 с.
3. Трофимова Т.И. Курс физики. - М.: Высш. шк., 1985. - 432 с.
4. Грабовский Р.И. Курс физики: Для с.х. вузов.- 5-е изд., переработ. и доп. - М.: Высш. шк., 1980. - 607 с.
5. Ландсберг Г.С. Оптика: Для физ. спец. вузов. - 5-е изд., переработ. и доп. - М.: Наука, 1976. - 928 с.
6. Лабораторный практикум по физике: Учеб. пособие для студентов втузов / под редакцией Ахматова А.С. - М.: Высш. шк., 1980. - 360 с.
ОГЛАВЛЕНИЕ
Введение 3
Общие положения о работе в оптической лаборатории 4
1. Изучение спектрального аппарата 6
2. Изучение явления дифракции 14
3. Определение раствора сахара с помощью сахариметра 27
Список литературы 39
ВОЛНОВАЯ ОПТИКА
Методические указания
к выполнению лабораторных работ
для студентов всех специальностей
Составители: Бакиева Диля Рашидовна
Гусева Зоя Николаевна
Дюков Валерий Владимирович
Кулакова Людмила Павловна
Гордеев Михаил Ефремович
Редакторы Л.С. Журавлева
И.П. Беляков
ЛР N 020302 от 18.02.97. ПЛД N 2018 от 05.10.94
Подписано в печать 12.05.99. Формат 60х84/16. Бумага тип. N 3.
Усл. п.л. 2,2. Уч. изд. л. 1,8. Печать офсетная (ротапринт).
Тираж 300 экз. Заказ N C- 59
Марийский государственный технический университет.
424000, Йошкар-Ола, пл. Ленина, 3
Отдел Оперативной полиграфии
Марийского Государственного Технического Университета.
424006 Йошкар-Ола, ул. Панфилова, 17
