Последовательность расчета.

4.1.1.1. Источники ЭДС Е1 и Е2 и включенные последовательно с ними сопротивления R1 и R2 заменяются источниками тока J1 и J2 c параллельно включенными сопротивлениями R1, R2.

J1 = Е1/ R1(4.1.1)

J2 = Е2/ R2(4.1.2)

Эквивалентная схема дана на рис. 4.

Рис. 4. Эквивалентная схема после замены источников ЭДС на источники тока.

4.1.1.2. Т.к. источники тока J1 и J2 включены параллельно, их можно заменить одним - Jэкв.; параллельно включенные сопротивления R1 и R2 - сопротивлением Rэкв.

Jэкв. = J1+J2(4.1.3)

1/Rэкв. = 1/R1+1/R2 (4.1.4)

Эквивалентная схема дана на рис. 5.

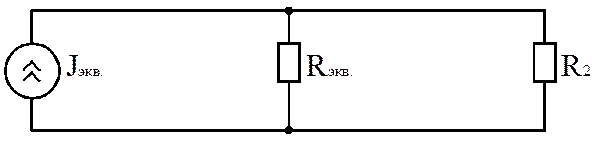
Рис. 5. Эквивалентная схема после замены нескольких источников тока

одним.

4.1.1.3. Источник тока Jэкв. и сопротивление Rэкв., включенное параллельно ему, преобразуются в источник ЭДС Еэкв. с внутренним сопротивлением Rэкв.

Еэкв. = Jэкв. Rэкв. (4.1.5)

что приводит к схеме, данной на рис. 6.

Рис. 6. Эквивалентная схема после замены источника тока источником ЭДС.

4.1.1.4. По закону Ома находится ток I3

I3 = Еэкв./ (Rэкв. + R3)(4.1.6)

Метод эквивалентного генератора

Суть этого метода расчета заключается в разделении схемы цепи на две части (см. рис. 7а) – одной из которых является участок с искомой величиной (R3), а вторая рассматривается как источник питания с ЭДС Ег. и внутренним сопротивлением Rг. (иначе - эквивалентный генератор, или активный двухполюсник).

Значения Ег. и Rг. по отношению к зажимам 1-2 цепи (см. рис. 7б) находятся расчетом левой части цепи с применением любого метода расчета электрических цепей, а ток через сопротивление Rх по закону Ома.

Iх = Ег./ (Rг. + Rх)(4.1.7)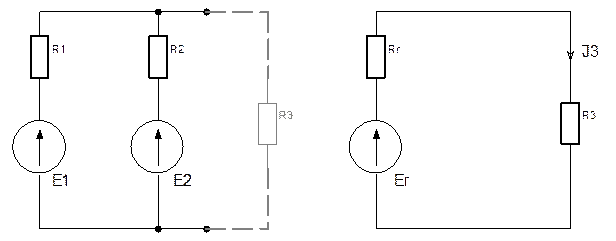

а) б)

Рис. 7. Схема к расчету цепи методом эквивалентного генератора.

Последовательность расчета

4.1.2.1. Определяется ЭДС Ег.эквивалентного генератора одним из методов расчета. Например, составив контурное уравнение по второму закону Кирхгофа

I1 (R1 + R2) = Е1 – Е2(4.1.8)

можно найти ток I1 = I2

I1 = I2 = (Е1 – Е2)/ (R1 + R2)(4.1.9)

Тогда

Ег. = U12 = Е2 + I2 R2(4.1.10)

4.1.2.2. Находится внутреннее сопротивление Rг. эквивалентного генератора, с учетом того, что по отношению к его зажимам 1-2 сопротивления R1 и R2 включены параллельно, т.е.

Rг. = R1 R2/ (R1 + R2) (4.1.11)

4.1.2.3. По закону Ома находится ток I3

I3 = Ег./ (Rг. + R3)(4.1.13)

Метод узловых потенциалов

Этот метод основан на определении потенциала каждого узла по отношению к какому-либо одному, принятому за базовый с нулевым потенциалом, а напряжение между любыми двумя узлами находится как разность их потенциалов. Обычно этот метод используется для расчета цепей с двумя узлами, но может использоваться и для расчета более сложных цепей.

Последовательность расчета

4.1.3.1. Определяется напряжение U12 между узлами 1 и 2 (см. рис. 7а) по выражению

U12 = (Е1G1 + Е2G2 + Е3G3)/(G1 + G2 + G3),(4.1.14)

где G1,G2 и G3–проводимости ветвей цепи.

4.1.3.2. По закону Ома находится ток I3.

I3 = U12/R3(4.1.15)

Метод суперпозиции

Расчет электрической цепи методом суперпозиции (наложения) сводится к последовательному исключению всех источников питания, кроме одного, при этом исключаемые источники питания заменяются их внутренними сопротивлениями; производя расчет упрощенной цепи, находят токи в ее ветвях, создаваемые каждым источником питания. Иначе эти токи можно назвать частичными. Полный ток каждой ветви находится как алгебраическая сумма частичных токов.