Ошибки округления при использовании метода трапеций

Граф вычислительного процесса для метода трапеций изображен на рис. 3. Предполагается, что все члены суммы, которые необходимо умножить на 2, сначала складываются, а их сумма умножается на 2. При этом не только экономится машинное время, но и уменьшается общая ошибка округления.

Пусть δ_i (i = 0, 1,..., п) — относительная ошибка каждой величины y_i. Пусть а_i (i = 0, 1, ...,n) — относительная ошибка округления при выполнении каждого из n + 1 сложений. На рис. 3 сложениям присвоены порядковые номера, поставленные около кружков со знаком «плюс». Например, а₂ есть относительная ошибка округления при выполнении сложения.

Наконец, пусть μ_i — относительная ошибка округления при выполнении умножения (y₄ + у₂ + ... + y_n-1) на 2, и пусть μ₂ — относительная ошибка округления при выполнении умножения (у₀ + 2y₁ + ... + 2y_n-1 + у_n) на h/2. Тогда относительная ошибка округления I_h принимает вид

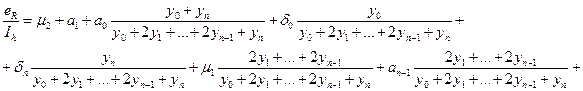
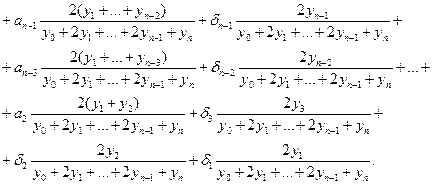
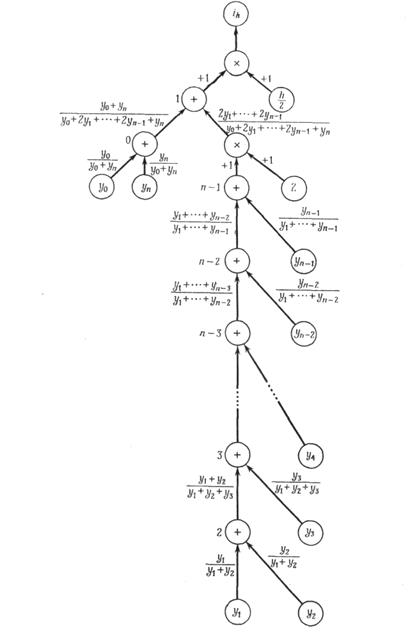
Рис. 3. Граф вычислительного процесса для интегрирования

по правилу трапеций.

Абсолютная ошибка равна

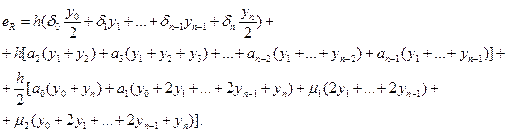
Теперь предположим, что 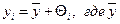равно среднему из всех значений y_i и 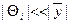, так что можно пренебречь членами, содержащими произведения 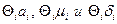. Кроме того, предположим, что

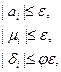
где ε - относительная ошибка округления при выполнении арифметической операции (мы уже записывали ее в виде 5•10^-t) а φ — некоторая постоянная, определяющая соотношение между ошибками исходной информации и ошибка­ми округления. Тогда

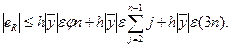
Но так как 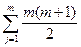, то формула для ошибки приобретает следующий вид:

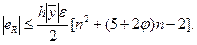
Но ведь 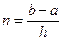, поэтому

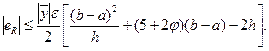
Очевидно, при малом h первый член из заключенных в скобках значительно превосходит по своей величине оба остальных члена, поэтому в качестве верхней границы возможной ошибки e_R можно принять выражение

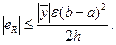(15)

Итак, мы получили интересный результат: верхняя граница для возможной ошибки округления возрастает как 1/h и при некотором h превосходит ошибку ограничения, пропорциональную h². В действительности сама ошибка округления возрастает медленнее, а именно пропорционально h^-p, где 0 < р < 1, но все же при достаточно малом h становится больше ошибки ограничения.

Это очередной поучительный пример расхождения между теорией и практикой вычислений. Теоретически можно сделать I_h сколь угодно близким к I, взяв h достаточно малым. Однако на практике ошибки округления ставят предел достижимой точности результата интегрирования.

В качестве примера рассмотрим интеграл

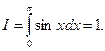
На рис. 4 изображена зависимость общей ошибки E_I от числа интервалов n.

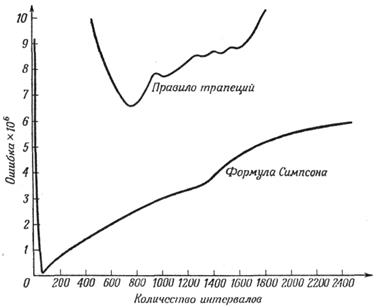
Рис. 4. Зависимость суммарной ошибки (ограничения и округле­ния) от количества интервалов при интегрировании sin x от 0 до π по правилу трапеций и по формуле Симпсона.

Зависимость эта определена для правила трапеций и правила Симпсона, которое будет рас­смотрено в разд. 6. Заметьте, что с возрастанием nобщая ошибка, равная сумме ошибок ограничения и округления, уменьшается до п = 775. После этого ошибка округления доминирует: увеличение п приводит к росту общей ошибки.

Наконец, заметим, что 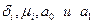не дают вклада в величину члена, зависящего от 1/h в формуле для e_I.

Вся ошибка, выражаемая этим членом, возникает во время суммирования

,

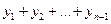так что нет смысла повышать точность вычисления самих величин y_i

Эту ошибку можно существенно уменьшить, производя сложение с удвоенной точностью, в то время как остальные операции будут выполняться с обычной точностью. Такой метод называется вычислениями с частич­ной удвоенной точностью.