Регулярный режим охлаждения (нагревания) тел
Полученные решения задач для тел различной геометрической формы показывают, что они имеют одинаковую структуру, т.е. представляют собой сумму бесконечного ряда, члены которого расположены по быстро убывающим экспоненциальным функциям. Например, для безграничной пластины при ее охлаждении в среде с постоянной температурой и постоянным коэффициентом теплоотдачи экспонента будет убывать пропорционально времени 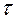
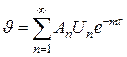 ,
,
где 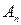 - постоянная, зависящая от формы тела и начального распределения температуры;
- постоянная, зависящая от формы тела и начального распределения температуры; 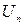 - функция координат, характеризующая пространственное распределение температуры и состоящая из физических характеристик тела; m – постоянная величина, растущая с ростом n и зависящая от формы и размеров тела и условий теплообмена с окружающей средой; n=1,2,3… .
- функция координат, характеризующая пространственное распределение температуры и состоящая из физических характеристик тела; m – постоянная величина, растущая с ростом n и зависящая от формы и размеров тела и условий теплообмена с окружающей средой; n=1,2,3… .
При малых значениях 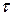 от 0 до
от 0 до 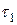 распределение температуры внутри тела и скорость изменения во времени температуры зависят от особенностей начального распределения условий температур. В этих условиях поле температур в теле будет определяться не только первым, но и последующими членами ряда.
распределение температуры внутри тела и скорость изменения во времени температуры зависят от особенностей начального распределения условий температур. В этих условиях поле температур в теле будет определяться не только первым, но и последующими членами ряда.
Первый период охлаждения, при котором скорость изменения температуры внутри тела зависит от вида начального распределения температуры, называют неупорядоченной стадией процесса охлаждения. С увеличением времени ряд становится быстросходящимся.
Начиная с некоторого момента времени 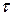 >
> 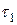 начальные условия начинают играть второстепенную роль и процесс полностью определяется условиями охлаждения на границе тела и среды, физическими свойствами тела и его геометрической формой и размерами. Эта стадия называется регулярным режимом. Температурное поле описывается
начальные условия начинают играть второстепенную роль и процесс полностью определяется условиями охлаждения на границе тела и среды, физическими свойствами тела и его геометрической формой и размерами. Эта стадия называется регулярным режимом. Температурное поле описывается
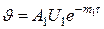 .
.
Логарифмируя это выражение, получим
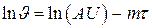 ,
,
т.е. натуральный логарифм избыточной температуры для всех точек тела изменяется во времени по линейному закону.
При длительном охлаждении, если 
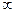 все точки тела принимают одинаковую температуру, равную tж,, т.е. наступает третья стадия режима охлаждения - стационарный режим.
все точки тела принимают одинаковую температуру, равную tж,, т.е. наступает третья стадия режима охлаждения - стационарный режим.
Таким образом, весь процесс охлаждения можно разделить на три стадии: неупорядоченный, регулярный и стационарный режимы.
Рассмотрим более подробно вторую стадию охлаждения.
После дифференцирования обеих частей последнего уравнения по времени получаем
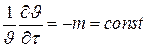 .
.
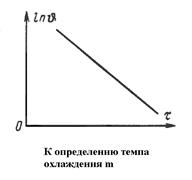
Левая часть этого выражения представляет относительную скорость изменения температуры и равна постоянной величине m, не зависящей ни от координат, ни от времени. Величина m измеряется в 1/с и называется темпом охлаждения. При наступлении регулярного режима темп охлаждения не зависит ни от координат, ни от времени и является постоянной величиной для всех точек тела; зависит только от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела.
Если экспериментально определить изменение избыточной температуры во времени и построить зависимость в полулогарифмических координатах, то темп охлаждения в стадии регулярного режима определяется как
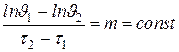 .
.
 Первая теорема Кондратьева. Выражение для зависимости темпа охлаждения m от физических свойств тела, его геометрической формы и размеров, а также условий теплообмена на поверхности тела можно найти из анализа теплового баланса
Первая теорема Кондратьева. Выражение для зависимости темпа охлаждения m от физических свойств тела, его геометрической формы и размеров, а также условий теплообмена на поверхности тела можно найти из анализа теплового баланса
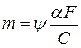 ,
,
где 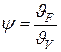 - коэффициент неравномерности распределения температуры,
- коэффициент неравномерности распределения температуры, 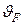 - средняя избыточная температура поверхности тела в данный момент времени,
- средняя избыточная температура поверхности тела в данный момент времени, 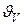 - средняя избыточная температура по объему;
- средняя избыточная температура по объему; 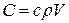 - полная теплоемкость.
- полная теплоемкость.
Из выражения следует, что относительная скорость охлаждения (темп охлаждения) однородного и изотропного тела при конечном значении коэффициента теплоотдачи 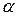 пропорциональна коэффициенту теплоотдачи, поверхности тела и обратно пропорциональна его теплоемкости. Последнее выражение представляет собой первую теорему Кондратьева.
пропорциональна коэффициенту теплоотдачи, поверхности тела и обратно пропорциональна его теплоемкости. Последнее выражение представляет собой первую теорему Кондратьева.
В уравнении множитель 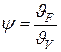 зависит от условий охлаждения на поверхности тела. Выясним характер зависимости коэффициента
зависит от условий охлаждения на поверхности тела. Выясним характер зависимости коэффициента 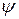 от числа Bi.
от числа Bi.
1) Bi→0. Это условие соответствует внешней задаче, когда распределение температуры в теле не зависит от его размеров и физических свойств. Следовательно, усредненные по поверхности и объему температуры будут одинаковы 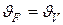 . Коэффициент неравномерности распределения температуры
. Коэффициент неравномерности распределения температуры 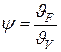 =1.
=1.
2) Bi→∞. При этом условии задача становится внутренней и процесс охлаждения определяется только размерами тела и его физическими свойствами. В силу большой интенсивности теплообмена температура на поверхности тела принимает постоянное значение, равное температуре окружающей среды. Коэффициент неравномерности распределения температуры 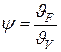 =0.
=0. 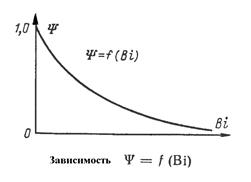 Следовательно, 0<
Следовательно, 0< 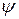 <1.
<1.
Вторая теорема Кондратьева. При Bi→∞, или 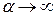 , темп охлаждения m становится прямо пропорциональным коэффициенту температуропроводности тела
, темп охлаждения m становится прямо пропорциональным коэффициенту температуропроводности тела
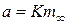 .
.
Коэффициент пропорциональности К зависит от геометрической формы и размеров тела
для шара 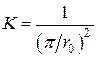 ,
,
для параллелепипеда 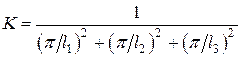 ,
,
для цилиндра конечной длины 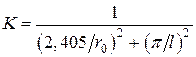 ,
,
для пластины 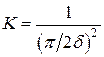 .
.
