Тема 3.5.2 Позиционные системы счисления, отличные от десятичной система счисления

Основанием позиционной системы может быть не только 10, но и другое число, р 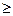2

– р – ичная система. Для записи чисел в р-ичной системе необходимо р знаков.

Определение. Записью натурального числа х в системе счисления с основанием р называют его представление в ви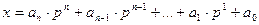де: , где 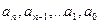принимают значения 0, 1,2, , р-1.

Задача. Сосчитать число клеток в фигуре в 3 – ичной и 5 –ричной системе счисления.

В 3- ичной системе используются знаки 0, 1, 2.

Счет: 1 один, 2 – два, 10 – один, ноль; 11 – один, один; 12 – один, два; 20 – два, ноль; 21 – два, один; 22 – два, два; 100 – один, ноль, ноль. Всего: 100₃

В 5 – ричной системе: 1, 2, 3, 4, 10, 11, 12, 13, 14. Всего: 14₅

Сравнение происходит также как и в десятичной системе счисления. 2101₃ < 2102₃

Арифметические действия происходят по тем же правилам, что и в 10 – ной системе. Нужно иметь таблицы сложения однозначных чисел в 3 – ичной системе:

+

Таблица сложения в 4- ричной системе

+

Используя таблицу можно складывать любые числа. 1221₃ + 122₃=2120₃

Выполнять вычитание: 2110₃ – 212₃ = 1121₃

Таблица умножения в 3- ичной системе:

х

Пример: 122₃* 22₃= 12001₃

Таблица умножения в 5- ричной системе:

х

Деление выполняется на основании таблицы умножения.

Пример: 10011₃ : 12₃=122₃

Одно и тоже число может быть записано в любой системе счисления. Нужно уметь осуществлять переход из одной системы в другую.

Теория: Пусть дана запись числа в системе счисления с основанием р, т.е.

.

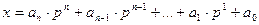Найдем запись этого числа в 10 – ричной системе счисления. Можно записать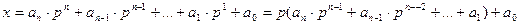

а₀ – остаток, меньший р. Дальше можно получить, что а₁ – остаток и т.д.

Т.о. запись числа находят так: Число х делят ( в 10 –ной системе) на основание р; остаток, полученный при делении дает последнюю цифру а₀ в р-ичной записи числа х; неполное частное снова делят на р, новый остаток дает предпоследнюю цифру р –ичной записи числа х; продолжив деление найдем все цифры р – ичной записи числа х.

Пример: Перевести число 2436 в 8- ричную систему счисления.

2436 = 304*8+4 = (38*8+0)*8 +4 = 38*8²+ 0*8 +4 =(4*8 +6)*8² + 0*8 +4 = 4*8³ + 6*8² + 0*8 + 4 = 4604₈

Показать делением уголком. 2436| 8

4 304| 8

0 38| 8

6 4 отсюда с последнего частного, а затем остатков идет запись числа 4608 в восмиричной системе счисления.

Пример.Выполним действия в указанных системах счисления:

а) 5 034₇ + 4 652₇; б) 3 214₅ • 12₅; в) 3 005₈ : 103₈.

Пример. Переведем число в систему счисления с новым основанием:

а) 10 212з в десятичную систему счисления;

б) 285 из десятичной системы в четверичную.

Решение, а) Для перевода числа 10 212з в десятичную си­стему счисления воспользуемся способом умножения. Для этого представим число в виде суммы разрядных единиц:

10 212₃ = 1 • З⁴ + 0 • З³ + 2 • З² + 1 • 3 + 2,

а затем выполним в новой десятичной системе счисления все действия, указанные в правой части равенства. При этом полу­чим 10 212₃ = 104.

б) При переводе числа 285 в четверичную систему счисле­ния удобнее использовать способ деления. Для этого разделим с остатком 285 на 4 — основание новой системы счисления, за­тем полученное частное снова разделим на 4 и т.д., пока деление возможно. Запись остатков в обратном порядке и даст нам пред­ставление числа 285 в четверичной системе счисления. Все дей­ствия при этом будут выполняться в наиболее привычной для нас десятичной системе счисления.

Следовательно, 285 = 10 1314₄