Математические головоломки
1. Сколько треугольников изображено в геометрической фигуре? (35)
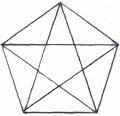
2. В три хода.
Положить на стол 3 кучки спичек. В одну кучку положить 11 спичек, в другую - 7, и в 3-ью - 6. Перекладывая спички из любой кучки в любую другую, надо сравнять все три кучки, чтобы в каждой было по 8 спичек.
Это возможно, так как общее число спичек - 24 - делится на 3 без остатка. При этом необходимо соблюдать правило: к любой кучке необходимо добавлять ровно столько спичек, сколько в ней есть. Например, если в кучке 6 спичек, то и добавить к ней можно только 6, если в кучке 4 спички, то и добавить к ней можно только 4. Задача решается в 3 хода.
Примечание: Вместо спичек могут быть использованы счетные палочки, пуговицы, другие предметы.
Ответ:
1) Из кучки где находится 11 спичек, берем 7 и перекладываем в кучку к 7 спичкам; в первой кучке осталось 4 спички;
2) Из второй кучки, где у нас получилось 14 спичек, берем 6 спичек и перекладываем в 3-тью кучку где имеется 6 спичек. В третьей кучке у нас получилось 12 спичек, во второй - 8 (первый результат);
3) Из третьей кучки, в которой 12 спичек берем 4 спички и перекладываем их к 4-ем спичкам, оставшимся в первой кучке. Во всех трех кучках получилось одинаковое число спичек - по 8.
3. Раздробить на части.
Раздробите число 45 на четыре части так, что если к первой части прибавить 2, от второй отнять 2, третью умножить на 2, а четвертую разделить на 2, то все результаты будут равными.
Ответ: Искомые части 8, 12, 5 и 20.
4. Какой знак надо поставить между написанными рядом цифрами 2 и 3, чтобы получилось число, большее двух, но меньшее трех?
Ответ: Запятую; получится 2,3.
5. Из спичек (счетных палочек) выложена цифра 14. Как превратить ее в цифру 5, переложив только одну спичку (счетную палочку)?

Ответ:

6. Сколько раз можно прочитать слово "ОРХИДЕЯ" в представленной фигуре?
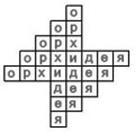
Ответ: 128 раз.
7. Берем 12 спичек (палочек) и выкладываем из них "равенство", как показано на рисунке. Как видите, "равенство" 6 - 4 не может равняться 9. Как переложить одну спичку так, чтобы получилось правильное равенство? Задача решается несколькими способами.

Первый ответ:

Второй ответ:

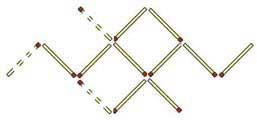
8. На рисунке изображен «жук» из 10 спичек. Необходимо изменить направление движения жука, переложив всего три спички (счетные палочки).

Ответ:
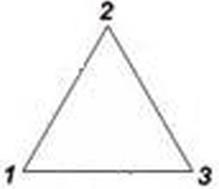
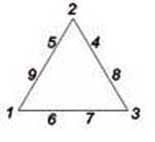
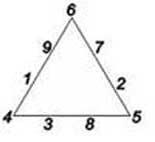
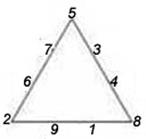
9. В вершинах треугольника помещены числа 1, 2 и 3. Разместите числа 4, 5, 6, 7, 8 и 9 по сторонам треугольника (по две цифры на каждой стороне) так, чтобы сумма всех чисел вдоль каждой стороны треугольника равнялась 17. Это нетрудно, так как известны числа в вершинах треугольника.
А попробуйте разместить числа 1, 2, 3, 4, 5, 6, 7, 8 и 9 вдоль сторон треугольника (по четыре цифры на стороне) так, чтобы сумма чисел на каждой стороне треугольника равнялась 20.
Числа в вершинах треугольника будут другие. В первом и втором случаях числа не повторяются и должны размещаться только по одному разу. Расположение чисел по сторонам треугольника может быть разнообразным.
Ответ:
10. На рисунке расположено 9 точек. Необходимо перечеркнуть их четырьмя прямыми линиями, не отрывая карандаш от бумаги.

Список литературы
1. Андреева Е. А. Лучшие в мире загадки и трехминутные развивающие игры для детей. – М.: РИПОЛ классик, 2006. – 320 с.
2. Волкова С.И. Тетрадь с математическими заданиями. – М.: Просвещение, 1993. – 158 с.: ил.
3. Жикалкина Т.К. Система игр на уроках математики в 1 и 2 классах четырехлетней начальной школы. – М.: Новая школа, 1995. – 176 с.: ил.
4. Ковалько В. И. Младшие школьники на уроке: 1000 развивающих игр, упражнений, физкультминуток (1-4 классы). – М.: Эксмо, 2007. – 512 с.
5. Кудыкина Н.В. дидактические игры и занимательные задачи. – К.: «Ряданська школа», 1990. – 142 с.
6. Панкратова Н.В. Развитие речи младших школьников //Нач. школа. № 6, 2001 г.
7. Тупичкина Е.А. Игра стимулирует воображение и фантазию детей.// Нач. школа. .№ 11, 1992 г.
8. Федин С. Н. Веселые игры и головоломки. От 4 до 9 лет. – М.: Айрис-пресс, 2005. – 240 с.: ил.
