Доказательства результатов из параграфа 2.

3.1. Используемые операторы. Для изучения начальной задачи (2.1), (2.5) потребуется оператор

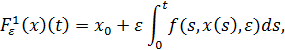
(1)

действующий в пространстве 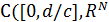). Соответствующий оператор для задачи (2.3), (2.6) действует в том же пространстве и имеет вид

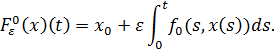
(2)

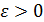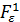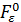При условии непрерывности оператора fпо совокупности переменных при каждом фиксированном операторы и вполне непрерывны в пространстве 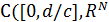) и их неподвижные точки являются решениями соответствующих начальных задач.

В задаче о Т- периодических решениях системы (2.1) применяется оператор

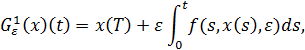
(3)

действующий в пространстве 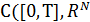). При каждом фиксированном с оператор (3) также вполне непрерывен и его неподвижные точки определяют, после Т- периодического продолжения на всю ось, Т- периодические решения системы (2.1) (см. [7]).

3.2. Индекс интегральной воронки.Рассмотрим уравнение

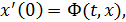
(4)

где оператор 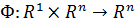и непрерывен по совокупности переменных.

3.3. Предложение. Пусть интегральная воронка уравнения (4) с начальным условием

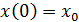
(5)

ограничена на отрезке [0, d]. Тогда индекс множества неподвижных точек оператора F, действующего в пространстве 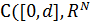) и задаваемого формулой

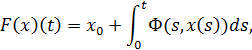
(6)

равен 1.

Доказательство. Обозначим через 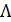множество решений задачи (4), (5) на отрезке [0, d]. Множество неподвижных точек оператора (6) в пространстве 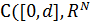) совпадает с 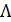. Пусть U – произвольное ограниченное открытое множество пространства 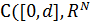), содержащее 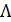. Множество 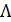замкнуто. Поэтому Fне имеет неподвижных точек на 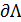. Кроме того, оператор 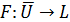, где L–замкнутое, выпуклое подмножество пространства 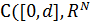), определяемое равенством

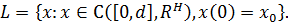
По теореме о сужении 1.3

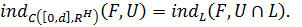
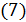
Продолжим функции из множества 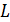на отрезок 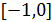константой по непрерывности. Рассмотрим оператор 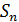, определяемый на множестве 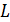равенством

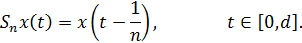
Возьмем произвольную функцию 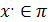. Положим

.

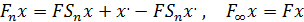Поскольку операторы 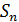сильно сходятся к тождественному оператору, то операторы 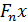вполне непрерывны по совокупности переменных, 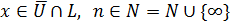. Покажем, что операторы 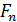и 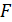при достаточно больших 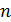линейно гомотопны на 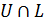. Допустим противное. Тогда существуют последовательности 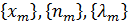такие, что 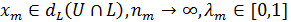и

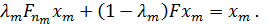
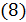
Из последнего равенства следует

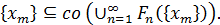
и, следовательно относительно компактна. Без ограничения общности можно считать, что 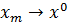, а 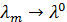. Перепишем равенство 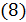более подробно

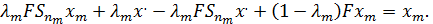
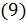
В силу непрерывности оператора 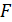и сильной сходимости операторов 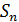к тождественному оператору в равенстве 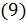можно перейти к пределу при 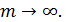Тогда получим 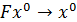и 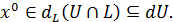В чем противоречие. Итак, в силу свойства 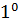п.1.2 и равенства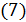

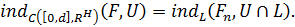
при достаточно больших .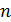

Покажем, что отображение 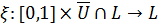и задаваемое формулой

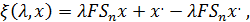
Является гомотопией, соединяющей операторы 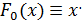и 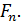Действительно, полная непрерывность оператора 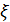вытекает из полной непрерывности оператора 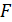. Кроме того при любом 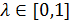уравнение

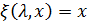
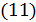
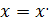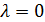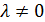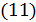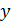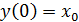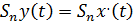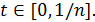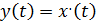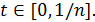Имеет единственное решение . При последнее очевидно, а при , если уравнение имеет решение , то , следовательно, при Поэтому при Тогда 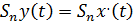при 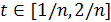.Продолжая далее, придем к равенству 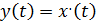при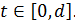

Для завершения доказательства осталось воспользоваться свойствам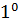и и 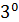п. 1.2. Тогда

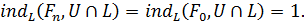
Учитывая равенство 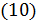, находим

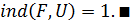
3.4. Доказательство теоремы 2.1.Обозначим через 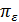множество решений задачи 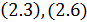на отрезке 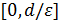. Пусть 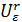- -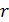раздутие множества 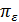в пространстве 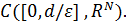Покажем, что при достаточно малых 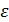операторы 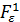и 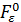, определенные формулами 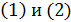, линейно гомотопны на множестве 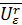в пространстве 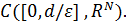Допустим противное, тогда существуют последовательности 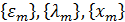такие, что

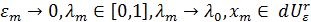
И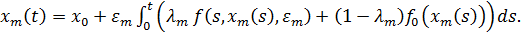

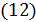
Делая в 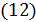замену переменных 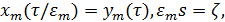получим, что для последовательности 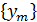пространства 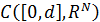справедливо 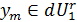и

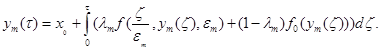
(13)

Заметим, что последовательность { 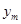} относительно компактна как сумма постоянной и двух ограниченных равностепенно непрерывных последовательностей. Без ограничения общности будем считать, что 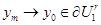, т.е. 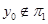. В силу Т-периодичности по t оператора f в равенстве (13) можно перейти к пределу при 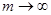. Тогда

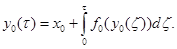
т.е. 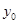- решение при ε=1 задачи (2.3), (2.6) на отрезке [0,d], не принадлежащее 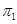, в чем противоречие. Итак, операторы 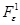и 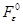гомотопны. Так как в силу предложения 3.3

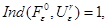
то в силу свойства 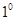индекса (см. п. 1.2)

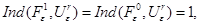
и по свойству 4 индекса оператор 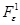имеет в 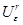неподвижную точку, а задача (2.1), (2.5) – решение на отрезке [0, d/ε].

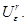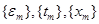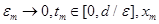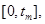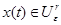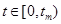Для доказательства неравенства (2.7) покажем, что при достаточно малых ε все решения задачи (2.1), (2.5) определены на [0, d/ε] и лежат в Допустим противное, тогда существуют последовательности такие, что - решение задачи (2.1), (2.5), определенное на отрезке причем при и 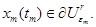Заметим, что в силу T- периодичности по t оператора f и его непрерывности по совокупности переменных существует константа M>0 такая, что

,

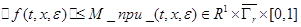(14)

где 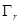- r- раздутие множества 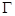, определенного в п.2.3. Поэтому 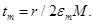Без ограничения общности можно считать, что последовательность точек 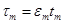сходится к некоторому 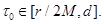Функции 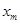на отрезках 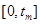удовлетворяют уравнению

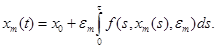
(15)

Делая в (15) замену переменных 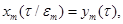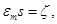получим, что для последовательности функций 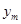, определенных на отрезках 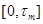, справедливо 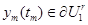и

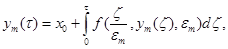
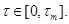
(16)

Будем считать, что функции 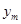определены на отрезке 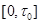, продолжив, если это необходимо, их с отрезка 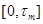на отрезок 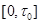по непрерывности константой. За таким продолжением сохраним прежнее обозначение. Заметим, что последовательность 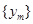относительно компактна в пространстве 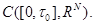Без ограничения общности будем считать, что 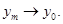Тогда 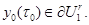В силу T-периодичности по t оператора f в равенстве (16) можно перейти к пределу при 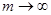. Тогда

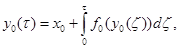
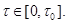
т.е. 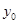- решение при ε=1 задачи (2.3), (2.6) на отрезке 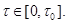Все решения задачи (2.3), (2.6) при ε=1 определены на отрезке 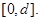Поэтому решение 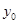может быть продолжено на отрезок 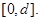Но так продолженное решение не принадлежит 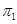, так как 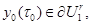в чем противоречие.∎

3.5. Доказательство замечания 2.3. При доказательстве теоремы 2.1 все рассуждения проводились в случае, когда аргументы оператора f лежат в множестве 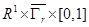(напомним 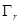- r- раздутие множества 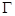, определенного в п.2.3 ). Поэтому и непрерывность оператора f достаточно потребовать на множестве (2.9).∎

3.6. Доказательство замечания 2.4. Периодичность оператора f была использована при доказательстве теоремы 2.1 при предельном переходе в равенствах (13) и (16), а так же при получении оценки (14). В условиях замечания 2.4 предельный переход обеспечивается леммой М.А. Красносельского - С.Г. Крейна (см. [7]), а оценка (14) вытекает из ограниченности оператора f на множестве (2.9).∎

3.7. Доказательство теоремы 2.5. В пространстве 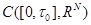рассмотрим ограниченное открытое множество 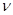, определяемое формулой

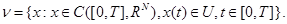
(17)

Покажем, что при достаточно малых ε на множестве 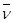оператор 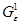, заданный формулой (3), линейно гомотопен оператору

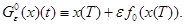
Допустим противное. Тогда существуют последовательност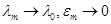и и 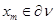такие, что

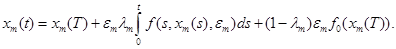
(18)

Заметим, что 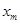непрерывно дифференцируемы и

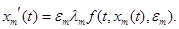
Так как 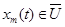, то 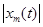равномерно ограничены, поэтому в силу непрерывности оператора f имеем

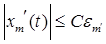
(19)

Где С – некоторая константа. Следовательно, последовательность 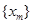вполне ограничена. Будем считать, что 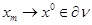,тогда в силу оценки (19) функция 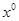- константа, т.е. 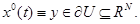Полагая в равенстве (18) t=T и деля на ε, получим

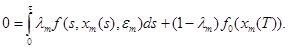
Переходя к пределу при 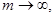найдем

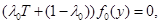
т.е. 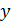– решение уравнения

,

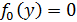(20)

лежащее на границе множества 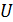, в чем противоречие. В силу свойства 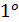индекса (см. п. 1.2)

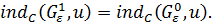
Оператор 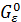отображает 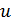в подпространство функций констант изоморфное 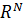. Поэтому, применяя теорему о суждении 1.3, будем иметь

?

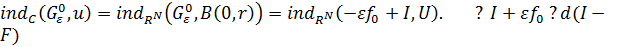Поскольку уравнение (20) не имеет решений, принадлежащий 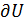, оператор 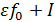гомотопен оператору 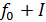. Гомотопия задаётся формулой

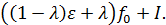
Итак,

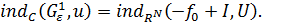(21)

Воспользовавшись свойством 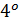индекса п. 1.2, получим, что при достаточно малых ε система ( 2.1.1) имеет -периодическое решение 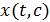, лежащее в ,

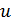т.е. 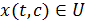при .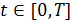

Пусть теперь 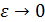, и последовательность при ( 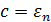) 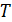-периодических решений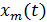

Системы (2.1), лежащих в 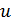, равномерно сходится к некоторой предельной функции 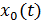. Тогда для функции 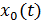справедлива оценка (19). Поэтому 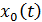- функция константа. Пусть 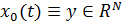. Так как 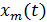- -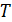периодическое решение системы (2.1), то для них выполнено равенство

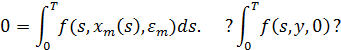
Переходя в последнем равенстве к пределу при 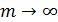, получим, что 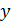является решением уравнения (20), т.е. состоянием равновесия.

Следствие 2.6 вытекает из теоремы 2.5, если в качестве множества 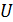взять .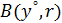

Следствие 2.7 следует из теоремы 1.4.

Литература

1. Ахмеров Р.Р., Каменский М.И. Ко второй теореме Н.Н.Боголюбова в принципе усреднения для функционально- дифференциальных уравнений нейтрального типа // Дифференц. Уравнения. – 1974. – 13. – с. 537-540.

2. Ахмеров Р.Р., Каменский М.И., Родкина А.Е., Потапов А.С., Садовский Б.Н. Меры некомпактности и уплотняющие опертаоры. – Новосибирск: Наука, 1986.

3. Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. –М.:Наука, 1974.

4. Гурова Н.Н. Одно утверждение типа принципа родственности и вторая теорема Н.Н. Боголюбова в принципе усреднения параболических уравнений // Качественные методы исследования операторных уравнений. – Ярославль, 1982. –с. 47-58.

5. Каменский М.И. О принципе усреднения для квазилинейных параболических уравнений с запаздыванием. // Доклады Академии наук. – 1994. – 337,N3. –с. 304-306.

6. Климов В.С. К задаче о периодических решениях операторных дифференциальных включений // Известия АН СССР. Математическая серия. 1989. -53, N2. – c.309-327/

7. Красносельский М.А., Забрейко П.П. Геометрические методы нелинейного анализа. –М.: Наука, 1975.

8. Красносельский М.А., Крейн С.Г. О принципе усреднения в нелинейной механике // Успехи мат. наук. – 1955. -10, N 3(65). – с. 147-152.

9. Потапова Л.В. Принцип усреднения и периодические решения параболического уравнения с запаздывающим аргументом // Укр. мат. ж. -1985. -37, N2. –c.198-205.

10. Самоленко А.М. Численно-аналитический метод исследования периодических систем обыкновенных дифференциальных уравнений. I, II // Украинский математический журнал. 1965. -17, -4. –с. 82-93; 1966. -18. -2. –с. 50-59.

11. Стрыгин В.В. Одна теорема о существовании периодических решений систем дифференциальных уравнений с запаздывающим аргументом // Мат. заметки. – 1970 . – 8. N2. –c. 229-233.

Содержание

§1. Теория топологического индекса вполне непрерывных операторов………………….2

§2. Классические первая и вторая теорема Н.Н. Боголюбова- Н.М. Крылова с формулировкой условий в терминах топологического индекса……………………………....3

§3. Доказательства результатов из параграфа 2………………………………………………………….6

Составитель Каменский Михаил Игоревич

Редактор Кузнецова З.Е.

Тираж 100 экз. Множительная техника математического факультета ВГУ